RDP 2005-11: A Small Model of the Australian Macroeconomy: An Update Appendix B: Econometric Issues
December 2005
- Download the Paper 628KB
In this appendix we address two econometric issues, discussion of which was deferred from the main body of the paper.
Covariance-correlation Matrix of the Equation Residuals
The first relates to the variance-covariance and correlation matrices of the residuals from the model's six behavioural equations, when estimated separately using OLS. As noted in Section 2 these equations do not exhibit any simultaneity, which might require us to estimate them as a system so as to avoid obtaining biased coefficients. However, the residuals from one equation might still display some correlation with those from another, which would indicate that a system estimator such as Seemingly Unrelated Regressions (SUR) would be preferable to estimating each equation independently.
To assess this, Table B1 below – which updates the corresponding table on page 43 of Beechey et al – takes the various equation residuals and shows the correlations between them above the main diagonal, their variances along the main diagonal and the covariances between them below the main diagonal.[43]
| Output gap | Real exchange rate | Import prices | Unit labour costs | Weighted median inflation | Headline inflation | |
|---|---|---|---|---|---|---|
| Output gap | 0.3221 | −0.0138 | 0.0262 | −0.1972 | 0.1900 | −0.1108 |
| Real exchange rate | −0.0219 | 7.9416 | 0.0186 | −0.0179 | −0.0557 | −0.0295 |
| Import prices | 0.0119 | 0.0418 | 0.6540 | 0.1118 | −0.0223 | 0.0986 |
| Unit labour costs | −0.0484 | −0.0218 | 0.0391 | 0.1914 | 0.0043 | 0.0608 |
| Weighted median inflation | 0.0135 | −0.0195 | −0.0021 | 0.0002 | 0.0186 | 0.3944 |
| Headline inflation | −0.0149 | −0.0195 | 0.0173 | 0.0065 | 0.0135 | 0.0660 |
Consistent with Beechey et al the estimated residuals from the real exchange rate equation display by far the largest variance, while those from the consumer price equations display the smallest. As might be expected, the largest absolute correlation coefficient of 0.39 arises between the two sets of inflation residuals. There are also moderate correlations between the residuals from the output gap and unit labour cost equations, and between those from the output gap and underlying inflation equations.[44] The other cross-equation correlations are very small.
These results suggest that the only sets of equations we might wish to estimate as part of a system would be the inflation equations as a pair and/or, to a lesser degree, the output gap, unit labour cost and underlying inflation equations as a trio. However, when these blocs of equations are estimated using SUR, we find that this has only a very small effect on any of the coefficient estimates or their statistical significance. We conclude that it is unnecessary to estimate the model as a system.
The Vertical Long-run Phillips Curve Condition in the Unit Labour Cost Equation
In Section 2.4 we noted that the model's potential output data are constructed concurrently with estimation of its unit labour cost equation, Equation (5). Hence, standard econometric tests of significance for coefficients in this equation are rendered technically invalid by the generated regressor problem, making it complicated to test whether or not a vertical long-run Phillips curve restriction is accepted by the data over the equation's whole estimation sample, 1977:Q1 to 2005:Q1.
To do so formally would involve a bootstrapping procedure to first create multiple sets of ‘pseudo data’ for unit labour costs (as well as for headline and underlying inflation), and then generate distributions for the estimated values of the parameters in Equation (5) – with no verticality restriction imposed – by applying the iterative procedure outlined in Section 3.1 and Appendix A to each pseudo data set. However, rather than pursue such a complex and time-consuming Monte Carlo simulation procedure, we content ourselves with a much simpler, if only indicative, test of the likelihood of accepting the verticality restriction in Equation (5).
This indicative test rests on the fact that the high smoothness parameter used in the model's new multivariate Hodrick-Prescott filter for estimating potential output allows only very gradual, long-lived changes in the estimated growth rate of potential output over history. The filtering process is therefore unlikely to be over-fitting the model equations used to condition it – including the unit labour cost equation – to any serious degree.[45]
An illustration of this point is provided by Gruen et al (2002), in which a closely analogous multivariate filtering procedure was used to generate vintages of potential output and output gap data, conditioned on Phillips curves for underlying inflation (each of which was required to satisfy a long-run verticality condition). In that case, with a similarly high choice of smoothing parameter, bootstrapping tests suggested that the Phillips curve coefficients were ‘not subject to significant biases’, and that the generated regressor problem was unlikely to be causing the statistical significance of these coefficients to be seriously misrepresented (Gruen et al, footnote 5, p 8 and Appendix B).
Thus, while not strictly correct, it seems likely that standard tests of the verticality restriction in Equation (5), ignoring the generated regressor issue, should still provide a broadly reliable guide as to whether or not this restriction is accepted by the data. When such a test is carried out, the freely estimated sum of the relevant coefficients, over the whole sample 1977:Q1 to 2005:Q1, is 0.975, which is not significantly different from 1. Hence, the verticality restriction appears to be easily accepted by the data.[46]
Footnotes
These statistics are based on data over the period 1985:Q1 to 2005:Q1, with the exception of those involving residuals from the inflation equations, which cover 1992:Q1 to 2005:Q1. [43]
The former likely reflects that non-farm output data are used to construct the unit labour costs data. Both results may also partially reflect that the unit labour cost and underlying inflation equations are used to condition the model's estimates of the output gap. [44]
Technical details of this issue are discussed briefly in Section 3.1 and Appendix A. However, the basic principle is akin to that which holds for ordinary Hodrick-Prescott filtering. In that case, if the filter's smoothing parameter is low then the filter of a series will closely match the original series, as there is little penalty for closely fitting even quite volatile original data. The analogue here is that, if our multivariate filter's smoothness parameter were low, this would result in an output gap profile yielding near-optimal overall goodness of fit of the filter's conditioning equations. Conversely, with a high smoothing parameter, the filter is strongly penalised for trying to over-fit these equations if this requires a volatile profile for estimated potential output. [45]
Formally, the test reported here involves replacing the imposed coefficient of 0.25
on the term 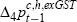 on the right-hand side of Equation (5) with a freely estimated one, and then re-estimating
the equation using the iterative procedure outlined in Appendix A.
This leaves all coefficient restrictions implicit in Equation (5), other
than the verticality restriction, intact. When this is done the freely estimated
coefficient on
on the right-hand side of Equation (5) with a freely estimated one, and then re-estimating
the equation using the iterative procedure outlined in Appendix A.
This leaves all coefficient restrictions implicit in Equation (5), other
than the verticality restriction, intact. When this is done the freely estimated
coefficient on 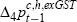 is 0.244, with a reported standard error
of 0.009.
[46]
is 0.244, with a reported standard error
of 0.009.
[46]