RDP 2005-11: A Small Model of the Australian Macroeconomy: An Update 1. Introduction and Overview

Almost a decade ago David Gruen and Geoff Shuetrim constructed a small macroeconomic model of the Australian economy. Details of this model were first presented publicly at a one-day symposium on monetary policy in June 1996. Four years later a comprehensive description of the then-current version of the model was provided by Beechey et al (2000). Since 2000, however, the model has continued to evolve, and the purpose of this paper is to provide an update on the current structure of the model and the major changes which have been made to it since Beechey et al.

One thing which has not changed over the past five years is the philosophy underpinning the model. It remains small, highly aggregated, empirically based, and non-monetary in nature. Its smallness means that it continues to provide a framework for thinking about the Australian economy which, unlike most models, can be ‘carried around in one's head’. Nevertheless, it remains rich enough to encompass many of the subtleties of the interactions between key variables in the Australian economy. In particular, it retains a well-defined long-run steady state with appropriate theoretical properties, despite most commonly being used to study macroeconomic developments over a short-run horizon of one to three years.^[1]

The model now consists of six estimated (or behavioural) equations – one more than in 2000. Two of these equations continue to concern real variables: real non-farm output and the real exchange rate. The remaining four (previously three) explain nominal variables. These are: import prices, nominal unit labour costs, and two different measures of consumer prices – a headline and a (new) underlying measure.

All six equations are specified so as to enforce theoretically desirable long-run behaviour, overlaid with short-run dynamics. For five of the six, this is achieved by means of an equilibrium correction framework; for the sixth (the unit labour cost equation), by the imposition of a vertical long-run Phillips curve constraint. To ensure appropriate steady-state behaviour, suitable restrictions are placed on certain coefficients in each of the model's nominal equations, as discussed in greater detail in Section 2.

1.1 Structure of the Model

Macroeconomic models lie along a spectrum, from the purely data-driven at one extreme to the wholly micro-founded at the other.^[2] The current model continues to lie at the empirical end of this spectrum, with its behavioural equations all econometrically estimated (subject to the handful of coefficient restrictions just mentioned).

With the addition of only one behavioural equation since 2000, the highly aggregated nature of the model has also been maintained. In particular, non-farm output continues to be modelled as a single entity, rather than disaggregated into its standard expenditure components. This represents a deliberate decision intended to maintain the simple, linear structure of the model.^[3] The model continues to be distinguished from typical small vector auto-regression models by the fact that, in addition to its six behaviourally determined endogenous variables, a further 19 exogenous variables appear in one or more of its estimated equations.

Finally, the model retains two other features of its previous structure. First, it remains non-monetary in nature, for the same reasons as discussed in Beechey et al (2000); as such, a short-term real interest rate continues to be used to measure the stance of monetary policy. Secondly, it continues to include no rational (model-consistent) expectations, although a forward-looking component of inflation expectations is allowed for through the inclusion of bond market inflation expectations in the model's unit labour cost equation.^[4]

Overall, the current model contains 33 variables (not counting growth rates of levels series as distinct variables). These may be broken into three categories: 19 exogenous variables (those whose future behaviour is pre-specified, in advance of solving the model); 6 behaviourally determined endogenous variables (forecasts of which are determined by econometrically estimated behavioural equations); and finally, 8 non-behaviourally determined endogenous variables (whose forecast profiles are determined by accounting identities involving behaviourally determined endogenous variables). The relationships between these variables are summarised in the flow chart shown in Figure 1 (where the model's behaviourally determined endogenous variables are shown in bold type, while shaded boxes indicate exogenous variables). An initial feel for the main changes to the model since Beechey et al (2000) may be obtained by comparing this flow chart with Figure 5 of that paper.

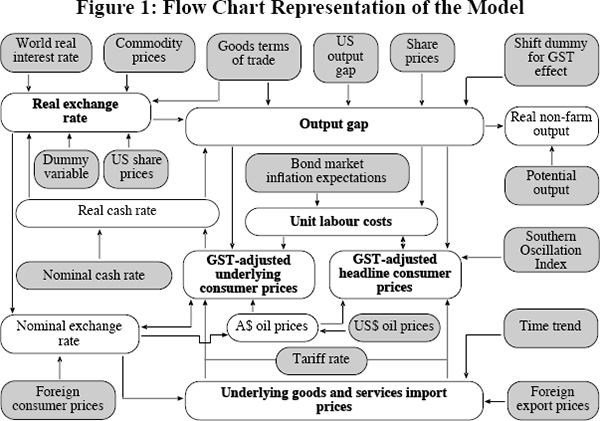
Monetary policy is modelled as affecting the economy through several channels. Changes in the nominal cash rate result in corresponding changes to the real cash rate, the level of which affects output both directly and indirectly (through its effect on the real exchange rate).

Non-farm output growth is now inferred from forecast changes in the output gap – the difference between (log) actual and potential non-farm output – rather than modelled directly. Specifically, forecast output growth is derived from changes in the output gap, together with an exogenous assumption about the future potential growth rate of the economy.^[5] The output gap is modelled as a function of: lags of the real cash rate; changes in the real exchange rate; changes in the terms of trade for merchandise goods; a measure of share prices; a dummy variable to capture the effect of the introduction of the Goods and Services Tax (GST) in July 2000; and a measure of foreign demand.

The output gap in turn influences the nominal side of the economy, directly affecting both consumer prices and unit labour costs. The latter are influenced not only by the gap, but also by inflation expectations, which are modelled as a mixture of past consumer price and unit labour cost inflation and bond market inflation expectations. As in Beechey et al, unit labour costs are modelled using a Phillips curve which is required to be vertical in the long run so as to tie the steady-state growth rate of these costs to that of inflation (see Sections 1.2 and 2.4 for further details).

Likewise, for headline consumer price inflation we retain the modelling approach adopted in Beechey et al (2000), involving an equilibrium correction framework. The level of headline consumer prices is modelled as a mark-up over input costs, which are assumed to consist of unit labour costs, import prices and oil prices. Disequilibrium between the levels of these prices generates an impetus to headline inflation – over and above the impact of other short-run influences such as the output gap, oil price inflation and unit labour cost growth – which acts to gradually unwind such disequilibrium. The same basic framework is also used to model underlying consumer price inflation.

Finally, import prices are assumed to depend on the nominal exchange rate, foreign export prices and the average level of tariffs, while the real exchange rate is determined by the (merchandise goods) terms of trade and the real interest differential between Australia and the rest of the world (together with short-run influences from commodity prices and the performance of US shares). Note also that there are no arrows in the flow chart running from consumer prices and the output gap to the nominal cash rate. This reflects that, for the purposes of the chart, we have elected not to be explicit about any possible link between these variables and the setting of monetary policy, with the latter treated as purely exogenous at this stage. A variety of monetary policy reaction functions could, of course, be adopted to formalise such a link. One such reaction function – an optimal policy rule – is discussed in more detail in Section 3.3.

1.2 Main Changes to the Model since Beechey et al

Overall, there have been seven main alterations to the model since 2000 (some of which have already been mentioned in passing).

First, a further behavioural equation has been added to the model describing the evolution of a second measure of domestic consumer price inflation. In addition to the headline inflation measure previously incorporated in the model, an underlying measure – weighted median inflation – is also now modelled. Moreover, variables such as the real interest rate, previously computed as the difference between the nominal cash rate and headline inflation, are now computed using underlying inflation.

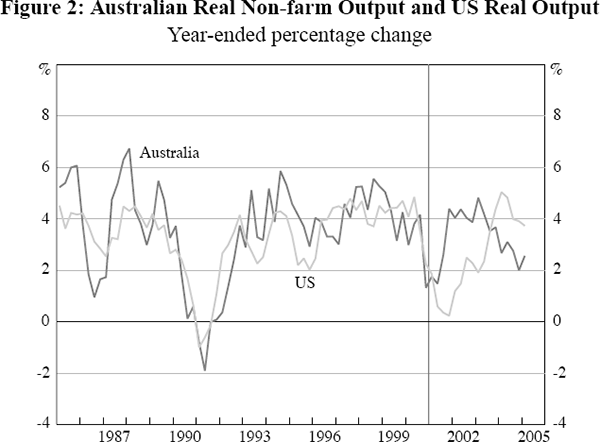
Secondly, the treatment of non-farm output growth has been changed from an equation based on a cointegrating relationship between the levels of Australian and US output, to one in which the non-farm output gap is instead modelled. Forecast output growth is then derived from the forecast behaviour of this gap, together with an exogenous assumption about the potential growth rate of the non-farm economy. The primary reason for this change is that, almost immediately following the publication of Beechey et al (2000), the strong correlation which had existed between Australian and US output growth over the 1980s and 1990s started to break down, as illustrated in Figure 2.

A third change to the model since Beechey et al (2000) is that the method used to estimate potential output (and hence also the output gap) over history has been altered. This is now carried out via a multivariate Hodrick-Prescott filter conditioned on developments in both unit labour costs and underlying inflation – see Section 3.1 and Appendix A for further details. One consequence of this change is that the vertical long-run Phillips curve condition in the model's unit labour cost equation can now be imposed over the whole sample for this equation, rather than just the latter part of it (as was the case in Beechey et al).

Fourthly, dummy variables associated with the impact of the introduction of the GST in July 2000 have been incorporated in the model's consumer price inflation and output gap equations. In the case of the model's inflation equations, the impact of the GST is modelled as leading to a one-off spike in inflation in the September quarter 2000, the magnitude of which is estimated, with an associated upwards shift of equal size in the level of the corresponding consumer price index. In the case of the output gap equation, the dummy variable is designed to capture the net effect of bring-forwards and deferrals of activity associated with the introduction of the tax.

A fifth change since June 2000 has been the inclusion, in the model's real exchange rate equation, of a further dummy variable covering the period mid 1999 to mid 2003. Inclusion of this dummy has been necessitated by the apparent temporary breakdown of the formerly strong relationship between the levels of Australia's trade-weighted real exchange rate and terms of trade. At the same time, the goods and services measure of the terms of trade previously used in both the model's real exchange rate and output equations has been replaced with a measure based on goods alone – for reasons outlined in Section 2.

Sixthly, definitional changes have been made to a number of series used in the model. Most notably, the import price series, formerly for goods, has been replaced by one for goods and services, so as to capture the impact of services import prices on consumer prices in the model's inflation equations.^[6] Similarly, the nominal exchange rate and foreign export price series used in the model's import price equation, formerly computed as G7 GDP-weighted averages, have been replaced with corresponding trade-weighted averages, in the hope of better reflecting the true mix of import price pressures in Australia resulting from either source.

Finally, the economy-wide unit labour cost series previously used in the model has been replaced by a smoothed version of the same series – with the chief aim of increasing the ‘signal-to-noise’ ratio of this series.^[7] In addition, where unit labour costs are used as an explanator in the model's headline and underlying inflation equations, the Balassa-Samuelson adjustment – for differences in the trend productivity growth rates of the traded and non-traded sectors of the economy – has been applied to this series, rather than to the model's import price series (as was done in Beechey et al 2000 for reasons of algebraic simplicity). Overall, therefore, the model now contains two principal measures of unit labour costs: a smoothed version of the economy-wide, national accounts-based series used in Beechey et al; and a Balassa-Samuelson adjusted version of this smoothed series, for use as an explanator in the model's consumer price inflation equations.

Footnotes

Within the Reserve Bank of Australia (RBA) the model is primarily used for policy analysis and research purposes (see Stevens 2001 for further details). [1]

As discussed in Beechey et al (2000), this spectrum exists because there is a trade-off between macroeconomic models' ability to fit the data and the degree to which they are rigorously based upon microeconomic foundations. While there has been some improvement over the past five years in the ability of carefully micro-founded models to replicate key features of the empirical data, a gap between the ends of this spectrum remains. [2]

Larger macroeconomic models which break output into its major expenditure (or production, or income) components almost invariably sacrifice linearity for the sake of the additional detail available from such disaggregation. Non-linearity arises because these expenditure components are typically modelled in logs, whereas the accounting identity under which total output is the sum of these components – a linear relationship – relates to the unlogged components. [3]

Calculation of the real interest rate and real exchange rate, however, remains based purely on current, rather than expected, domestic consumer price inflation – although underlying rather than headline inflation is now used. See Section 2 for further details. [4]

Over history, the potential growth rate of the economy, and level of potential output, are estimated via a multivariate Hodrick-Prescott filter conditioned on developments in both unit labour costs and underlying inflation. This estimation method differs from that used in Beechey et al (2000), and is described in detail in Section 3.1 and Appendix A. [5]

At the same time, the level of oil prices has now been included in the long-run components of each of the model's consumer price inflation equations. This change allows for the fact that the import price measure used in these equations remains an underlying one, which excludes petroleum prices. [6]

The smoothing itself is carried out using a 5-term Henderson moving average. For a more detailed discussion of the reasons for this change, see Section 2.4. [7]