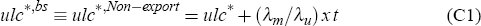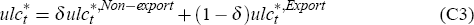RDP 2005-11: A Small Model of the Australian Macroeconomy: An Update Appendix C: Adjusting for the Balassa-Samuelson Effect

In modelling the impact of labour costs on domestic consumer prices, we ought to exclude those labour inputs ultimately associated with the production of exports – since the prices of these do not feed into domestic inflation. In industrialised economies there is an observed tendency for productivity to grow faster in the export sector than in the remainder of the domestic economy, which we refer to as the Balassa-Samuelson effect. All other things equal, such a productivity differential would lead the economy-wide growth rate of unit labour costs to understate the growth rate of those unit labour costs feeding into domestic consumer prices.

An adjustment for the Balassa-Samuelson effect was included in Beechey et al (2000). However, for reasons of algebraic simplicity this adjustment was made to the model's import price series, rather than to unit labour costs directly. By contrast, for reasons of transparency we apply this adjustment directly to the model's unit labour cost series. Hence, it is a Balassa-Samuelson adjusted version of ulc*, denoted ulc*^,bs, which now enters the model's consumer price inflation equations.

In line with the scale of correction adopted in Beechey et al, the Balassa-Samuelson adjustment we impose is given by

where x, the differential between the growth rate of unit labour costs in the export sector and in the remainder of the domestic economy, is taken to be 0.005 (0.5 per cent per quarter). This formula follows, in a manner analogous to the derivation in Beechey et al, from the assumptions that

and

together with the presumption that the ratio δ:(1 − δ) is proportional to λ_u:λ_m(where λ_u and λ_m are as specified in the model's consumer price inflation equations, Equations (6) and (7)).

The choice of x = 0.005 is based on an assumption that the productivity differential between the export and domestic sectors in Australia is the same as that in Australia's trading partners, so that x is equal to the average differential between foreign consumer price and export price inflation. This difference, on an annualised basis, was exactly 2.0 per cent per annum over the period 1992:Q1 to 2005:Q1, the sample used for estimating the model's inflation equations.^[47] The choice x = 0.005 is also quite close to the value we would obtain (viz 2.3 per cent per annum) were we to attempt to estimate x, using non-linear least squares applied to Equation (7), along the lines set out in Beechey et al.

Footnote

This choice for x is therefore also consistent with our steady-state assumption of a 2 per cent per annum differential between foreign consumer price and export price inflation, as well as with generating the steady-state model properties set out in Table 8. [47]