RDP 1999-09: Australian Banking Risk: The Stock Market's Assessment and the Relationship Between Capital and Asset Volatility 4. Results
November 1999
- Download the Paper 459KB
4.1 Financial Risk
A market estimate of the weighted-average capital-asset ratio is constructed to combine the individual bank results each month, with each bank weighted by its share of the total market value of assets. Weighted averages for each of the four cases considered, derived using historical estimates of equity volatility, are presented in Figure 3. In this figure the capital-asset ratio is defined to include the bank licence value [k = (A + φB − B)/(A + φB)] and thus captures both the tangible and intangible assets of the bank.
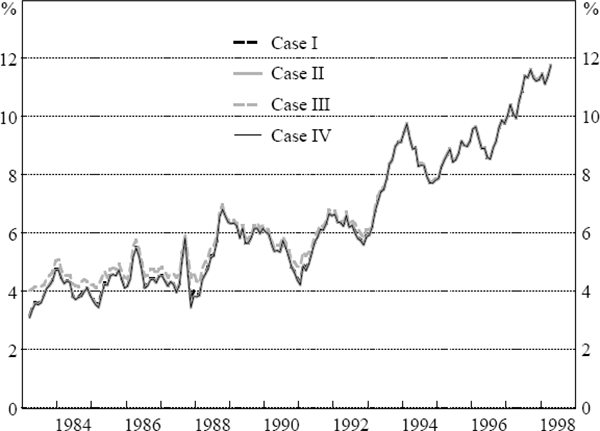
As found in Gizycki and Levonian, the estimated capital-asset ratio rose sharply in the late 1980s, after being at quite low levels in the preceding years.[19] Interestingly, this coincided with the introduction of the Basel risk-based capital adequacy standards. Following this dramatic increase, the capital-asset ratio fell during the years 1989–1991 before regaining its upward momentum. The estimates continued to trend upwards, rising particularly quickly over the periods 1991–1992 and 1993–1994. The capital-asset ratio ended the sample period at a level considerably higher than was observed in the early 1980s, suggesting that stock market participants are of the view that the financial risk of banks has decreased over this period.
The observed behaviour of this stock market based measure of financial risk differs considerably from that implied by the regulatory capital-asset ratio. The regulatory risk-weighted ratio (considered as an asset-weighted average across the banks in our sample) declined over the first half of the 1990s from around 11 per cent to a low of 8.3 per cent. From the second half of 1995 the ratio steadily increased to a level of 10.4 per cent by March 1998. The main source of difference in the two ratios follows from the differing treatment of capital. Our model estimate of capital (and in turn the capital-asset ratio) is strongly affected by the market capitalisation of each bank. In most years of the 1990s growth in Australian banks' market capitalisation was considerably stronger than the growth in book value equity (which is the basis for the regulatory ratio).
The secular pattern of the weighted-average capital-asset ratio is most heavily influenced by the four largest banks.[20] Individual bank results vary considerably, with some banks' capital-asset ratios rising significantly over the sample period and others remaining static or falling slightly.
4.2 Operating Risk
Figure 4 illustrates the weighted-average asset volatility, derived once again using historical estimates of equity volatility. The model's estimate of asset volatility is itself highly variable through time. The market's assessment of individual firms can change rapidly and frequently. The quality of the model's risk estimates is greatly dependent on the stock market's efficiency. Any tendency for price bubbles to develop that push share values away from economic fundamentals will undermine the model's accuracy. In particular, instances of market-wide movements driven by speculative dynamics may swamp assessment of the riskiness of individual firms. In this regard, the spikes in volatility surrounding the stock market corrections in 1987 and 1997 clearly greatly overstate the riskiness of banks' assets.
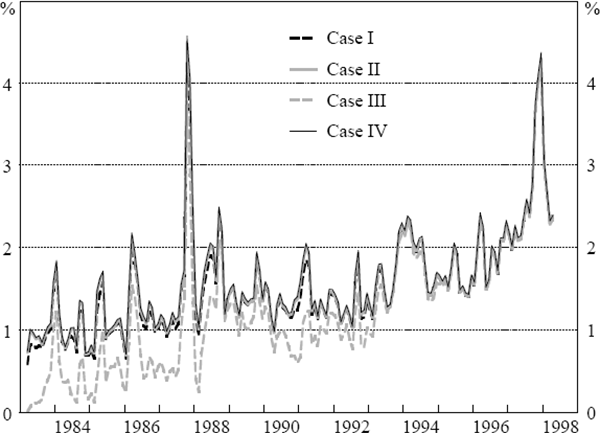
The slight upward trend in asset volatility during the 1980s, detected by Gizycki and Levonian, gathered momentum in the following decade. This finding contrasts strongly with the declines in banks' impaired assets and charges to profit and loss for bad and doubtful debts since the early 1990s, which suggest that the banks' primary risk exposure – credit risk – has fallen (see, for example, Ulmer (1997)). The patterns for the individual banks differ to some degree, although in no case is there substantial disagreement.
These results suggest that the stock market based measure of operating risk has increased over the sample period, mitigating to some extent the positive effect of increased capital on insolvency risk. The evolution of the probability of closure should give us a feel for which effect dominated.
4.3 Total Bank Risk
4.3.1 Probability of closure
The model's implied probability of bank closure is expressed as 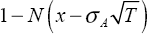 .
.
Figure 5 presents the average probability of closure across the 15 banks, when applying the Case III (high licence value and early closure) parameterisation of the model. To give an idea of the dispersion across the banks, the largest individual-bank estimate for each month is also shown.
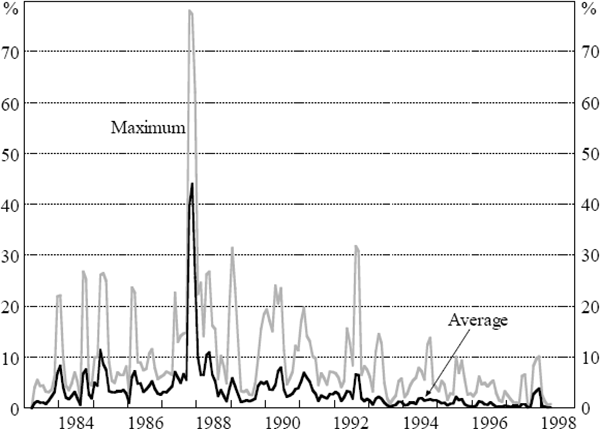
Not surprisingly, the effect of the 1987 stock market crash dominates the series. The sharp decline in share prices, coupled with extreme volatility around this time, combined to produce the aberrant result. The model assumes that such extreme volatility reflects a change in the markets' valuation of individual firms. However, market-wide speculative dynamics would seem to have dominated in this episode. Other notable features are the sensitivity of the results to the underlying data and the gradual decline in the series since 1990. The only blip in recent times has been the spike towards the end of 1997, reflecting the sudden fall in stock markets.
Despite the steady rise in the volatility of assets, observed in Figure 4, the market's assessment of the average probability of closure has declined over the years. It appears, therefore, that in the market's view the increase in operating risk has been more than offset by decreases in financial risk.
It seems reasonable to argue that the macroeconomic impact of an individual institution's failure depends on the proportion of the financial system that the institution accounts for (see, for example, Kent and Debelle (1998)). Given each bank's estimated default probability, it is possible to obtain the probability distribution of losing a given share of the banking system (as measured by the market value of assets). To do this we make the simplifying assumption that each bank's default probability is independent of all other banks.
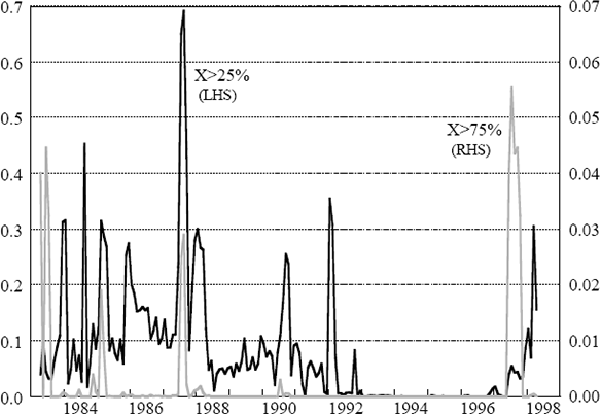
Figure 6 shows the probability of losing more than a quarter and more than three-quarters of banking assets in the year ahead. Once again, the period around the 1987 stock market crash dominates the results and, for the reasons discussed above, can be discounted as overstating true risk. For most of the 1990s the market's assessment of the probability of loss has been very low. The increases in the likelihood of loss seen from mid 1997 reflect recent spikes in sharemarket volatility.
4.3.2 Expected creditor losses
Annual averages of the sum, across banks, of the expected losses borne by creditors are presented in Table 2.[21] The assumptions employed in deriving these estimates (e.g. all liabilities, not just deposits, are insured) mean that whilst we can draw conclusions from movements in the series with a degree of confidence, not too much emphasis should be placed on their level.
| Year |
Case I (low licence value and early closure) |
Case II (low licence value and late closure) |
Case III (high licence value and early closure) |
Case IV (high licence value and late closure) |
|---|---|---|---|---|
| 1983 | 0.82 | 1.37 | 0.07 | 1.35 |
| 1984 | 3.22 | 6.20 | 0.18 | 6.09 |
| 1985 | 3.89 | 8.59 | 0.21 | 8.42 |
| 1986 | 2.47 | 4.64 | 0.26 | 4.57 |
| 1987 | 181.00 | 208.75 | 137.11 | 206.24 |
| 1988 | 4.42 | 6.79 | 1.36 | 6.69 |
| 1989 | 2.66 | 2.99 | 1.78 | 2.96 |
| 1990 | 1.06 | 1.47 | 0.44 | 1.45 |
| 1991 | 4.08 | 6.81 | 0.76 | 6.70 |
| 1992 | 22.74 | 35.50 | 3.85 | 35.02 |
| 1993 | 0.55 | 1.19 | 0.03 | 1.17 |
| 1994 | 0.68 | 0.90 | 0.17 | 0.88 |
| 1995 | 40.83 | 42.38 | 36.21 | 41.92 |
| 1996 | 0.51 | 0.57 | 0.27 | 0.56 |
| 1997 | 10.65 | 11.23 | 8.39 | 11.04 |
| 1998 | 0.57 | 0.61 | 0.32 | 0.60 |
Notes: In some years, the annual average of the total contingent
payout is materially affected by one or two outliers. For example: |
||||
Expected losses are negligible in most years. Notable exceptions are the large values recorded in 1987 and, to a lesser extent, in 1997 – both are the result of volatility in the stock market. Overall, the movements corroborate the conclusions reached from the analysis of the probability of closure.
4.4 Impact on Results of the Different Proxies for the Volatility of Equity
Figure 7 illustrates the impact on the results of using the forward-looking estimate of σE, obtained from options, when applying the Case III parameterisation of the model.
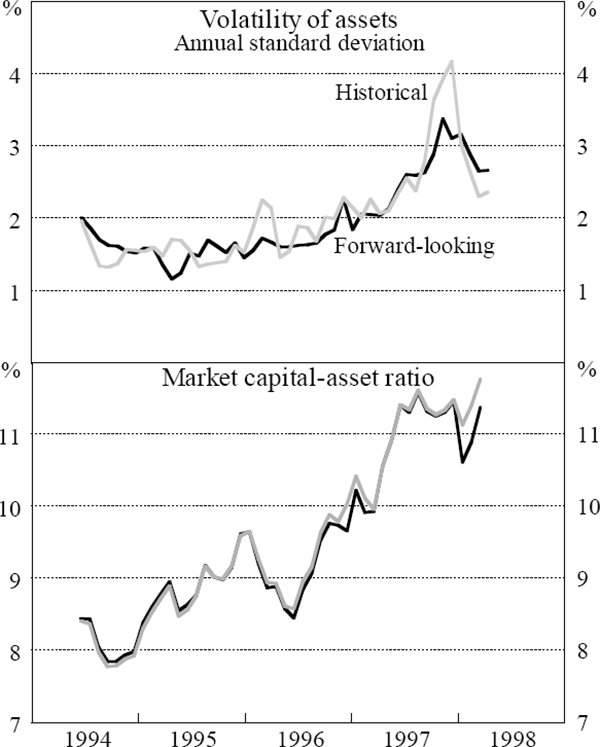
The market capital-asset ratio is not significantly affected by the choice of estimate. The volatility of assets, on the other hand, is dependent on the estimate employed; whilst the long-term movements are comparable, the series is more variable when the historical estimate is used. This is not entirely surprising given that the historical measure is itself more variable than the forward-looking measure (Figure 2 and Equation (7)). Although not shown, this difference is manifested in estimates of both the probability of closure and the deposit-guarantee liability; specifically, the estimated series have fewer spikes when the forward-looking measure of equity volatility is used.
4.5 Sensitivity of Results to Assumed Closure Threshold and Licence Value
The sensitivity of the results to the assumed closure threshold and licence value can be investigated by comparing the results for the four cases described in Table 1. Specifically, the sensitivity to a change in the closure threshold can be determined by comparing Case I with Case II and Case III with Case IV, while the impact of movements in licence value are borne out by contrasting Case I with Case III.
Figure 3 shows that the market capital-asset ratio is unaffected by variations in either the assumed closure threshold or the licence value. The licence value has no influence on the capital-asset ratio by construction. As stated earlier, the capital-asset ratio presented in Figure 3 incorporates both the tangible and intangible assets of the bank. For a given value of equity, any increase in intangible assets (i.e. a higher φ) will lead to a commensurate fall in tangible assets leaving total assets and, hence, the capital-asset ratio unchanged.
From Figure 4, a clear relationship between the volatility of assets and the calibrated parameters cannot be discerned. Before the early 1990s, it appears that the volatility of assets was influenced by the difference between the closure threshold and the licence value, rather than the level of either one of them. Since then, changes in the level of, and the difference between, the closure threshold and the licence value do not appear to have had any impact.
Turning our attention to Table 2, it can be seen that a higher closure threshold (i.e. the bank is closed earlier) reduces the contingent liability. This is to be expected since the closure threshold places a cap on losses. Increasing the licence value also reduces the public-sector liability. The sensitivity of the contingent liability to assumptions about c and φ make it inappropriate to attach much weight to the specific dollar amounts of the liability. The general pattern over time is, however, reasonably consistent across the four cases. There are analogous relationships between the calibrated parameters and the probability of closure.
Footnotes
Note that Gizycki and Levonian (1993) do not include the licence value in the capital-asset ratio calculation. [19]
The four largest banks are ANZ, Commonwealth Bank of Australia, National Australia Bank and Westpac. [20]
If the public sector were to guarantee deposits, then Table 2 could be interpreted as the deposit guarantee liability. [21]