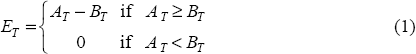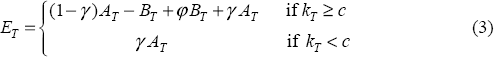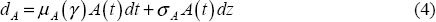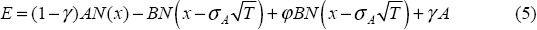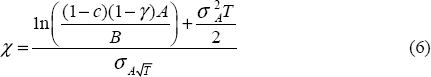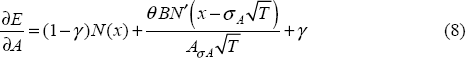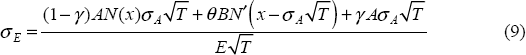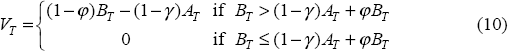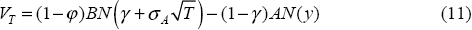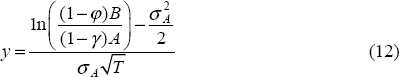RDP 1999-09: Australian Banking Risk: The Stock Market's Assessment and the Relationship Between Capital and Asset Volatility 2. Methodology

In this section we present the contingent-claim model used to derive four measures of bank risk, namely: (1) the volatility of the return on economic assets; (2) the economic capital ratio; (3) the probability of closure; and (4) the value of the potential public liability.^[1] Initially, we outline a contingent-claim model that can be applied to all leveraged firms. This model is then modified to accommodate bank-specific factors. We then explain how the model is estimated and discuss how the model is used to infer the aforementioned measures of risk.

2.1 A Contingent-claim Model of a Bank

Consider a firm that has assets with an economic value of A_T and liabilities with an economic value of B_T due at date T. If assets exceed liabilities at maturity of the debt, the firm will continue operating, with the value of equity being the difference between assets and liabilities.^[2] If, on the other hand, assets are less than liabilities, equity holders will relinquish control of the firm and draw on their position of limited liability; as a result, the value of equity has a lower bound of zero. Thus, the value of equity at date T is:

Equity is described as a contingent claim since a positive payoff to equity is contingent upon the bank being solvent at date T. At any time prior to T, the total market value of a bank's equity can be calculated using the same valuation techniques used to price other contingent claims, such as options. Equity holders are often viewed as having a long call option on the assets of the firm, where the strike price is equal to the face value of liabilities, because the payoff from such a position at maturity of the option is characterised by Equation (1).

Following Levonian (1991a), this basic model is augmented to capture factors that relate specifically to banks. The first adjustment to the model is to incorporate a bank ‘licence value’. This licence value captures the intangible asset value in a firm. Financial institutions that are granted a banking licence benefit from being called a ‘bank’. Specifically, the fact that banks are perceived to have some form of public-sector backing generally enables them to pay a rate of interest on deposits that is approximately equal to the risk-free rate, since depositors anticipate little risk of default.^[3] Furthermore, some customers are willing to pay an added premium to transact with banks since banks are viewed as being a superior source of both credit and debit services. It should be noted that these benefits of a banking licence are partially offset by compliance costs, since banks must abide by portfolio-constraining directives issued by the Australian Prudential Regulation Authority (APRA) (such as limits on the concentration of exposures to counterparties). Beyond these regulatory concerns, a large part of a bank's licence value will be due to its franchise value (value of its brand name or goodwill). Since such branding distinguishes each bank from the others, competitive forces do not necessarily drive the franchise value down to zero. In our model, the licence value is modelled as a constant fraction (φ) of liabilities and is received by equity holders at date T only if the bank remains open.^[4]

As in Cordell and King (1992), a second adjustment is made to account for the impact of dividends on the value of equity. The payment of dividends reduces assets and, hence, the value of the contingent claim, but it also transfers value directly to shareholders. In our model, it is assumed that dividends, γA_T are paid at date T.

The third modification allows for the fact that regulators have some discretion over whether a bank continues to operate – the so-called closure threshold need not be the point of actual insolvency, as was the case in Equation (1). In our model, regulators are assumed to monitor banks at discrete intervals with a view to deciding whether to close the bank (the present date is taken to be t=0 and the next monitoring date t=T).^[5] It is further assumed that regulators will close a bank if that bank's capital ratio, k_T, is less than c, where k_T is defined as:^[6]

If the bank's capital ratio is above the closure threshold, equity holders receive the full value of the bank as a going concern. If a bank remains open at date T, shareholders receive the dividend-adjusted difference between assets and liabilities ((1 − γ)A_T − BT), a lump sum equal to the rents conferred by a banking licence (φB_T) and a dividend payment (γA_T).^[7] This is the case regardless of whether the closure threshold is positive or negative.

If the bank is closed, it is assumed that equity holders manage to appropriate one final dividend payment from the firm. This assumption is made for algebraic convenience and, since dividend payments are small relative to total assets, does not materially affect our results. The full payout for equity holders, however, depends upon whether the closure threshold is positive or negative. If regulators only close banks with negative capital then, at closure the equity holders will only receive the final dividend (γA_T). If, however, regulators apply a positive closure threshold, then at time T, equity holders would receive the net tangible assets of the bank ((1 − γ)A_T − B_T + γA_T) – once the bank is closed the licence value falls to zero.

A number of countries (including the US and Japan) have introduced prompt corrective action schemes whereby troubled banks must be closed before book-value equity falls below zero. Nevertheless, the slippages that have been seen in the implementation of prompt corrective action schemes (see for example Benston and Kaufman (1998)), and the past experience of resolving troubled financial institutions in Australia, suggest that it can be difficult for regulators to close a bank at positive economic capital ratios.^[8] As a result, we exclude the possibility of closure at positive capital ratios from the model.

Reflecting adjustments for licence value, dividend payments and regulatory closure, the value of equity at the monitoring date, T, can be stated as:

where c is less than or equal to zero.

To obtain estimates of the value of equity prior to the monitoring date, it is necessary to make some assumptions regarding the stochastic processes followed by assets and liabilities. As in most contingent-claim models, assets are assumed to follow Geometric Brownian Motion. The change in assets, d_A, can be expressed as:

where t is a time index, μ_A is the expected instantaneous rate of return on assets per unit of time, σ_A is the instantaneous standard deviation of the rate of return on assets and dz is the differential of a Wiener process.^[9] Put simply, the first term on the right-hand side describes the drift of assets (or the average rate of return) over time while the second term can be regarded as adding noise or variability to the path followed by assets. For simplicity, the market value of liabilities is assumed to be constant. Provided that liabilities are repriced frequently, any move in interest rates will be offset by changes in future cash flows, leaving the present value of liabilities roughly constant. Any risk that does arise from liabilities (for example, from those with fixed payments) will appear in our estimate of the volatility of the return on assets.

An important determinant of the value of equity is the probability that the bank will close. The relationship between the key determinants of closure is delineated in Figure 1. For illustrative purposes, the figure is presented in the context of the basic model outlined in Equation (1).

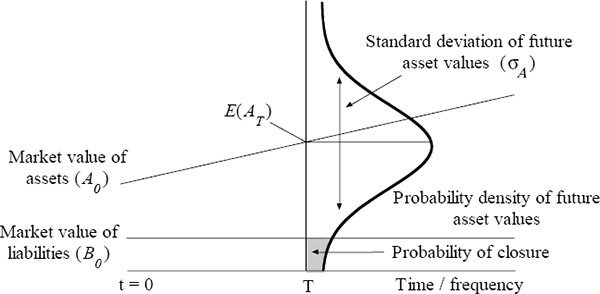
Knowledge of the current market value of assets and the stochastic process followed by assets makes it possible to estimate the distribution of asset values at the monitoring date. As Figure 1 shows, the probability that assets will be less than liabilities at the monitoring date depends on: (1) the expected value of assets at the monitoring date, E(A_T) (i.e. the first moment of the distribution); (2) the variability of assets (i.e. the second moment of the distribution); and (3) the level of liabilities. The shaded area of the distribution in Figure 1 represents this probability.

The Black-Scholes option-pricing formula incorporates all the factors described above in estimating the value of a contingent claim. Using this formula, the value of equity at date t=0 is:

where

N(·) is the cumulative standard-normal distribution function and variables without subscripts denote present values.^[10] As discussed previously, equity holders can be viewed as having a long European call option position in the value of the firm; equity holders have the option of either paying out the debt holders and acquiring the firm (receiving (1 − γ)A + φB + γA) or letting their claims to the firm expire (still receiving γA).^[11] The probability that this option will be exercised (i.e. the probability that the bank will remain open) is represented in Equation (5) by 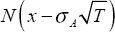. As mentioned earlier, the probability that the option is not exercised is illustrated by the shaded area of the distribution in Figure 1.

Given values for the market capitalisation of the firm (E), bank liabilities (B), the regulatory monitoring interval (T), the capital-ratio closure threshold (c), the licence value ratio (φ), and the rate of dividend payments relative to assets (γ), the two remaining unknowns in Equation (5) are the value of assets (A), and the volatility of assets (σ_A).^[12] Clearly, to compute the two unknowns a second independent equation is needed.

Marcus and Shaked (1984) suggest applying Ito's Lemma to the expression for the value of equity, to yield a second equation involving the volatility of equity and the volatility of assets. They follow Merton (1974) in deriving the relationship:

The basic idea of Equation (7) is that the volatility of a bank's equity is a magnified version of the volatility of a bank's assets, where the magnification factor depends on leverage and how changes in assets are divided between liabilities and equity (that is, the elasticity of equity to assets).^[13]

Differentiating Equation (5) with respect to A yields:

where N′ (·) is the standard-normal density function and θ=1/(1−c)−(1−φ).^[14] Using Equation (8), the relationship defined by Equation (7) can be expressed as:

If σ_E is observable, this equation also has A and σ_A as the only unknowns; hence, Equation (5) and Equation (9) can be solved simultaneously for values of these two variables. Thus, under the assumption that the value of bank equity is determined as in Equation (5), the market capitalisation of a bank can be used to infer the market value of assets and asset volatility.

2.2 Measures of Banking Risk

Given this theoretical framework, the central issue of this paper can be posed more explicitly. The key measure of the riskiness of a bank is the probability of closure. This overall risk measure can then be broken down into two components – ‘financial risk’ and ‘operating risk’. (The term ‘operating risk’ is used in the literature. It should not be confused with operational risk, which is the risk of earnings volatility not caused by market or credit factors.)

Financial risk is aligned with the bank's leverage. Regardless of the proclivity of banks to take risks, exogenous events can result in banks incurring large losses. A bank's ability to withstand such large losses will depend on its level of capital. In terms of Figure 1, financial risk is inversely related to the difference between the economic assets and liabilities of the firm (that is, the mean of the distribution relative to B₀). The second component of overall risk, which is denoted operating risk, increases if the volatility of assets increases. If a bank takes on a portfolio of assets characterised by a more uncertain income stream then, ceteris paribus, the chance of it incurring crippling losses increases. In Figure 1, this risk shows up in the shape of the distribution; specifically, closure is more likely, the more volatile the assets.

In addition to the probability of closure, we present an alternative measure of overall risk, the expected losses borne by banks' creditors. We include this measure for purposes of comparison as this measure is widely used in the literature. This measure originated in those countries where the repayment of deposits is guaranteed. For these countries (including France, Germany, Japan, United Kingdom and the United States), the losses borne by creditors are transferred to the deposit insurer. The expected creditor losses can, therefore, be thought of as the value of the deposit guarantee, or the expected amount that the guarantor will have to pay depositors at the monitoring date. In Australia, the system of depositor protection is quite different. While the Banking Act 1959 places a duty on APRA to exercise its powers and functions to protect depositors, the repayment of deposits is not guaranteed.^[15] Despite the absence of explicit depositor protection, market participants may hold the view that depositors are protected from financial loss, whether as a result of pre-emptive action by the supervisor, or due to compensation payments. Regardless of whether any liability is borne by a government authority or the debt holders themselves, the size of this contingent liability can be estimated in a similar way to how we estimate the value of equity.

For simplicity, it is assumed that all creditors of a failed bank will be protected from financial loss if a government authority steps in whenever equity holders do not exercise their option. This assumption enables us to treat the claims covered by any deposit guarantee as the total value of liabilities, B. If a bank fails, the payout under the guarantee may take the form of direct restitution to depositors. In this situation, the guarantor will liquidate the assets of the bank and will pay depositors the amount they are owed. When liquidating the assets on behalf of depositors, the guarantor is only able to sell the bank's tangible assets. Therefore, to compute the contingent liability under this scenario it is important to distinguish between the tangible assets of the bank, A, and the intangible assets, φB. An alternative approach which the guarantor could follow is to locate a purchaser for the failed bank; the acquirer would receive all assets of the bank – both tangible and intangible – and would assume all of the liabilities. If the assumed liabilities exceed the combined value of the tangible assets and the licence, the deposit guarantor makes up the difference.

The size of the contingent liability depends on which action the regulator is likely to choose. Clearly, the liability will be lower under the second scenario since the licence value is being used to reduce the payout to depositors following the bank's failure. As with the other risk measures, we are more interested in movements of the contingent liability rather than the level. Thus, given our assumption that the licence value is constant through time, our conclusions will not be affected by what action we assume the guarantor will take following a bank's failure. Since it seems likely that the guarantor would take the action that limits its liability wherever possible, we assume that the guarantor will find a purchaser for the failed bank. In this situation, the payout by the guarantor at the monitoring date, V_T, is:

The guarantor has sold a put option to equity holders that has the same characteristics as the long call option held by equity holders (i.e. same strike price, etc).^[16] If the value of the firm falls below liabilities, equity holders will exercise their put option and will force the guarantor to pay the debt holders the shortfall (of course, if the government does not step in, debt holders will suffer the loss – they can be viewed as having a short put option position). Using the Black-Scholes formula once again, the value of the contingent payout in Equation (10) is:

where

Therefore, once values for A and σ_A have been obtained it is straightforward to calculate the deposit-guarantee liability. Ceteris paribus, bank risk has increased if the size of this deposit guarantee has increased.

Footnotes

The application of this technique to leveraged firms was pioneered by Merton (1974), the central framework of which has been employed in a number of subsequent papers (see, for example, Markus and Shaked (1984) and Cordell and King (1992)). [1]

The value of a firm's economic liabilities (including equity) is equal to the value of a firm's economic assets, since the former represents a complete set of claims on the cash flows that accrue from the assets. [2]

Of course, protected deposits are still risky in the sense that the real return on deposits can fluctuate unexpectedly. [3]

The main motivation for assuming that the licence value is proportional to liabilities is technical modelling convenience. It is likely that the value is positively related to bank size. As will be discussed later, assets in the model are assumed to be stochastic; thus, if the licence value was related to assets in the model rather than liabilities, then its value would also be stochastic. This would introduce an additional element of random fluctuation into the value of shares, thereby complicating the theoretical development of the model without substantially adding to the analysis. The assumption is appropriate to the extent that the value of the licence reflects the opportunity to use deposits as a low cost source of funds. [4]

In this formulation, debt holders are assumed to play a passive role in the decision of whether the bank will be closed. One rationale for this assumption is that the operations of the bank are sufficiently opaque to prevent debt holders from observing the market value of the bank's assets. In this environment, debt holders are reliant on the supervisor to act in their best interests. [5]

The capital-asset ratio is defined exclusive of the licence value. It, therefore, captures only the tangible assets of the bank. For this reason, the firm can still be solvent with a capital-asset ratio less than zero. This is discussed further in Section 3.3. [6]

In a multi-period setting, φB and γA would reflect the discounted value of the future stream of rents and dividends respectively. [7]

Supporting this claim, the final annual report of the State Bank of Victoria gives a capital-asset ratio of about −0.06 when considering the State Bank group as a whole in the absence of government assistance. [8]

This assumption implies that assets have a log-normal distribution and, hence, the returns on assets have a normal distribution. [9]

Note that, for simplicity, we have assumed that the expected periodic rate of return on assets, μ_A, is equal to zero. [10]

Using standard option terminology: assets are the underlying security; liabilities are the strike price of the option; and the value of equity is the price, or premium, of the option. [11]

The values of E, B, T, C, φ and γ used in the estimation are discussed in Section 3. [12]

A substantial change in the market value of assets will influence the bank's probability of default and, therefore, the market value of liabilities. [13]

The partial derivative 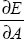is the delta of the option with respect to the underlying asset. [14]

The Act provides APRA with a range of powers designed to protect depositors. In particular, where a bank is likely to become unable to meet its obligations, the Act confers power on APRA to investigate the bank's affairs and assume control of the bank for the benefit of its depositors. The Act also provides that the assets of the bank in Australia shall be available to meet its deposit liabilities in Australia in priority to all other liabilities. For a more extensive discussion of APRA's powers and objectives see Goldsworthy, Lewis and Shuetrim (1999). [15]

In actual fact, the long call option position, discussed in Section 2.1, is equivalent to equity holders owning the assets of the firm and having a long put option in those assets. [16]