RDP 1999-09: Australian Banking Risk: The Stock Market's Assessment and the Relationship Between Capital and Asset Volatility 3. Data, Assumptions and Methods
November 1999
- Download the Paper 459KB
To derive estimates of the four risk measures, it is necessary to specify values for the following variables and parameters: σE, φ, c, E, B, γ, and T. This section focuses on these inputs to the model.
3.1 Estimates of the Volatility of Equity Returns
In our model we use both an historical, or backward-looking, estimate and a forward-looking estimate of the standard deviation of the rate of return on equity, σE.
3.1.1 Historical estimate
Traditionally, historical estimates have been used. In this paper, each month the historical estimate of σE is calculated as the annualised standard deviation of daily returns over the 50 days preceding the last day of the month. Our sample is comprised of 15 banks that were listed on the Australian Stock Exchange between January 1983 and April 1998. As at December 1998, these banks accounted for over 93 per cent of all Australian banks' assets. For the full list of banks see Appendix A.
3.1.2 Forward-looking estimate
Theoretically, the appropriate measure of volatility is the expected volatility of the return on equity over the life of the option (i.e. t=0 to t=T). Underlying the use of the historical measure is the assumption that expectations at each point in time are formed adaptively. Specifically, the historical measure used in this paper assumes that market participants base their expected level of volatility over the next year on the previous 50 days' realised returns. To the extent that market participants use additional information when forming their expectations of σE, the historical measure may be a poor proxy.
A more conceptually appealing alternative is to infer volatility estimates from the price of options written over individual bank share prices. The price of an option depends on the:
- price of the underlying asset;
- strike price;
- term to maturity;
- risk-free rate of return; and
- expected volatility of the underlying asset over the life of the option.
Given values for the first four determinants and the price of the option itself, numerical techniques can be used to calculate the expected, or implied, volatility. This implied volatility is then used as the estimate of σE.
Unfortunately, there are two principal drawbacks to using implied volatility estimates. Firstly, from a theoretical standpoint, we are interested in the expected volatility of the return on equity. However, options trade on individual shares and, therefore, only provide us with the expected volatility of the share price, σP. Provided that we are willing to accept the assumption that the number of shares on issue is constant, over the life of the option, then this is not a problem – σP will equal σE. Secondly, from a practical standpoint, the sample size is reduced substantially, since only six banks (Advance Bank, ANZ, Commonwealth Bank of Australia, National Australia Bank, St. George Bank and Westpac) have had options traded on their shares. As a consequence, the results may not fully reflect the riskiness of the banking sector as a whole. However, these six banks accounted for 89 per cent of all banks' assets (at December 1998) and thus, while being a more restricted sample than that employing share-price data, can be regarded as representative of the Australian banking market.
Day and Lewis (1988) point out two additional sources of potential bias in the use of option prices. Firstly, to correctly calculate the implied volatility, it is necessary to use contemporaneous share and option prices. However, in reality, the last option trade may not coincide with the last observed share price. Secondly, trades may occur at anywhere between bid and ask prices making it impossible to obtain a precise estimate. To mitigate the extent of these potential biases, we adopt Day and Lewis' suggestion of using estimates of implied volatility from a number of different options on the same stock. Specifically, we select those options that are either at- or near-the-money. This rule, which is similar to that adopted by Levonian (1991b), was chosen on the basis that trading volume is concentrated in these options: as trading volume increases, the problem of nonsynchronous trading will diminish, and the spread between the bid and ask prices will be reduced.
Ideally, options from which the volatility of equity is inferred should have a term to maturity of one year, this being the assumed length of the regulatory monitoring interval. However, this is not practical given the paucity of trading in options of this length. For reasons already given, we selected the more actively traded short-term options. Provided that volatility is not expected to change significantly in the period between the expiration of the option and the monitoring date, the implied volatility from these options should provide a reasonable estimate. However, Day and Lewis also point out that technical factors relating to the unwinding of hedged positions may distort option prices, and hence, volatility estimates, for those options near expiry. Following Levonian, we omit from our sample options with a term to expiry of less than approximately two months.
Implied volatility estimates were collected from the Australian Financial Review for every Wednesday over the period July 1995 to April 1998.[17] Monthly averages of the weekly estimates were then used for σE.
3.1.3 A comparison of equity volatility estimates
Figure 2 shows both the historical and implied volatility estimates used in this paper. Both measures are calculated by taking the simple average of the annualised volatility estimates for the six banks included in the options sample.
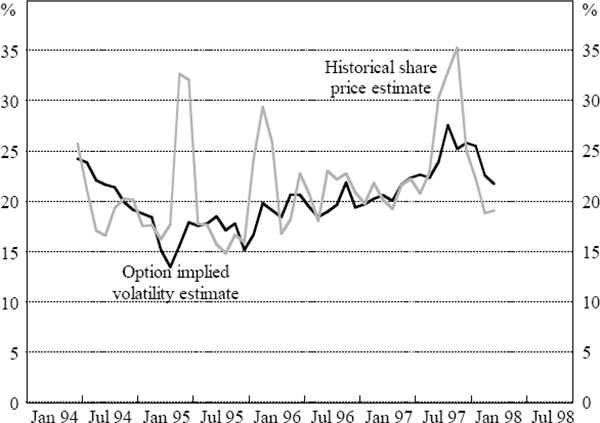
Whilst the long-term movements in the two series are comparable, the historical measure is considerably more variable. This reflects two facets of the estimates. Firstly, as mentioned earlier, the implied estimate assumes that the number of shares on issue is constant. Thus, a significant change in the number of shares on issue will only surface in the historical estimate. This helps to explain the large divergence between the two series in 1995. Specifically, the two measures reacted in contrasting ways to the capital raising undertaken by Advance Bank. The implied estimate reacted to the capital raising only to the extent that it contained information regarding the future volatility of the share price. The historical measure, on the other hand, reflected both the realised change in share price and the issue of additional shares. Secondly, the historical estimate places equal weight on all share-price movements in the preceding 50 days, regardless of the information content contained in them. The implied volatility estimate, on the other hand, reacts only to that information deemed relevant in formulating expectations on the future volatility of bank shares.
3.2 The Value of a Banking Licence
The value of a banking licence is likely to be revealed in interest rate spreads. On the liability side, the licence may enable banks to set a rate on their deposits which is less than the rate on government securities. Similarly, on the asset side, the licence may allow banks to earn a rate of return on their loans in excess of the rate required on the open market for securities of commensurate risk. Conceptually, we can use loan and deposit spreads to obtain a rough estimate of the licence value.
Levonian (1991b) demonstrates that the licence value can be approximated by
where Δ is the loan spread – the rate of return on loans held by the bank minus the required rate of return for assets with the same level of risk, rf − rd is the deposit spread – the rate on government securities minus the average cost of banks' liabilities, and k denotes the capital ratio. The difficulty in obtaining good measures of these spreads prevents us from generating accurate estimates of the licence value in Australia. A cursory look at some interest rate spreads suggests that the bank licence value is somewhere between 4 and 7 per cent of liabilities, depending on the capital ratio employed. Since substantial approximation error is likely, these estimates should only be regarded as a rough guide to the true licence value. In Section 4 we discuss the impact that the size of the bank licence has on the results.
Given the differences in size, geographical location and business strategies across the banks in our sample, it is likely that there are inter-bank differences in φ. However, the aggregated nature of the data available necessitates assuming that the licence-value ratio is identical across banks. We also assume that the licence value is constant over time.
3.3 The Closure Threshold
As discussed in Section 2, the basic contingent-claim model is augmented to reflect the fact that bank closures may not necessarily occur at the point of insolvency. Instead, we argue that regulators will close a bank if that bank's capital ratio falls below a pre-specified, negative, closure threshold. In searching for solutions to our systems of equations, we therefore assume that the closure threshold has an upper bound of zero. However, solutions for the system of equations could not be obtained for some banks at closure thresholds above −0.02. This suggests that the market views bank closures as being extremely unlikely at small negative values of capital. For this reason, we consider −0.02 to be a maximum value for the assumed closure threshold.
The capital ratio can become negative since it is defined exclusive from the licence value. We estimate the market value of assets and separate those assets that are intangible – the value of the banking licence – from those that are tangible, AT. In calculating the capital ratio we use tangible assets. Because we make this distinction, a bank can still be solvent at the monitoring date when AT < BT. There is, however, a limit on how low assets and, hence, the capital ratio can go. Specifically, the bank will become insolvent if liabilities are greater than the sum of tangible assets and the licence value. Because of this, we can place a lower bound on the closure threshold as a function of the licence value: the solvency condition, A + φB − B ≥ 0, implies that c ≥ − φ/(1 − φ)
3.4 Parameter Assumptions
Given the uncertainty surrounding the size of the licence-value ratio and the closure threshold, four different scenarios are considered in this paper.
Early closure describes the situation where banks are closed when the value of tangible assets is judged by the market to be lower than the value of liabilities, but the bank's intangible assets have not been exhausted (i.e. AT<BT but AT − BT + φBT ≥ 0). This highlights the differences between solvency judged on accounting, market-value and cash-flow bases. It is possible for a bank to be solvent when assessed against accounting measures of the value of assets and liabilities, but to be insolvent in market-value terms. It is also possible that a firm may be insolvent in either accounting or market-value terms but still have sufficient cash flow to remain in business for sometime. Late closure, on the other hand, occurs when banks are closed at the point at which the market value of tangible assets falls below liabilities by an amount equal to the value of the banking licence; that is, the licence value is fully exhausted. The robustness of the results to the different scenarios in Table 1 is analysed in Section 4.5.
| Early closure | Late closure | |
|---|---|---|
| Licence value relatively low | Case I | Case II |
| c = −0.02, φ = 0.04 | c = −0.04, φ = 0.04 | |
| Licence value relatively high | Case III | Case IV |
| c = −0.02, φ = 0.06 | c = −0.06, φ = 0.06 |
3.5 Equity, Liabilities, Dividend Payments, Monitoring Intervals and Estimation Techniques
The final step before the risk measures can be estimated is to assign monthly values for equity, liabilities, the rate of dividend payments relative to the value of assets and the monitoring interval. Equity is simply the monthly average of the bank's market capitalisation. The nature of a bank's liabilities enables us to assume that the book value of liabilities is equal to their economic value. Final and interim dividends paid by each bank are used to compute the dividend rate; hence, it is assumed that market participants perfectly forecast future dividends. Lastly, the monitoring interval is set equal to one year. This is consistent with APRA's practice of conducting an on-site review and a prudential consultation with each bank once per year (on average).[18]
The system of equations was solved using the GAUSS 1.49B procedure for solving non-linear equations. The algorithm employed is a modification of Broyden's secant method (Eldefsen and Jones (1986), Dennis and Schnabel (1983)), which combines Broyden's method with Newton's method, Newton's method being used when Broyden's approximation does not move towards the system's solutions.
Footnotes
The implied volatility estimates provided by the Australian Stock Exchange Options Market were used rather than taking option prices and inferring volatilities ourselves. [17]
It is possible that regulators might vary the closure threshold and, in particular, the monitoring interval according to the condition of each bank. The volatility of asset returns and the market capital-asset ratio are both increasing functions of the monitoring interval. [18]
