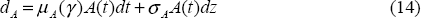RDP 1999-09: Australian Banking Risk: The Stock Market's Assessment and the Relationship Between Capital and Asset Volatility 5. The Relationship Between a Bank's Operating and Financial Risk
November 1999
- Download the Paper 459KB
The contingent-claim model used to derive asset volatility assumes that the market value of assets follows the Geometric Brownian Motion process set out in Equation (4). In particular, it assumes that, over the regulatory monitoring period, the volatility of assets is constant and that the level of assets (and hence, the capital-asset ratio) is independent of asset volatility (that is, μA is not a function of σA).[22] Since it is not possible to obtain analytical expressions for σA and A from Equations (5) and (9), it is difficult to determine those values of the model parameters that will generate a positive or negative relation between σA and A (and thus k). Moreover, the evolution of σA and A will reflect the dynamic behaviour of σE, γ, E and B, since we use updated estimates of these variables when solving for new values of σA and A. In this section we present a number of arguments which suggest that movements in a bank's capital-asset ratio and asset volatility will be related. We then go on to examine the empirical significance of that relationship and investigate its dynamics.
Whilst the theoretical relationship between a bank's operating risk and its capital has been the focus of numerous studies over the years, the literature has generated differing conclusions about how risk taking and capital are related. This section begins by reviewing the more popular hypotheses with the aim of establishing a framework within which the empirical results can be understood.
5.1 Risk-based Capital Adequacy Standards
The Basel risk-based capital adequacy standards explicitly link the amount of capital that banks are required to hold with the riskiness of their assets. Under the initial standards, adopted by the Reserve Bank of Australia in 1988, the appropriate level of capital was deemed to be 8 per cent of risk-weighted assets. The risk weights were designed to measure the relative degree of credit risk attached to various groups of assets. An elaboration of the 1988 guidelines, which came into effect in 1998, means that banks are now required to hold capital against their market-risk exposures in addition to that held to support credit risk.
Although the risk-based capital arrangements are by no means perfect (the risk weights are rough rules of thumb; for example, all non-government corporate enterprises are given a 100 per cent risk weighting), we would expect that those banks engaging in riskier activities would be required to hold a larger amount of capital. That is, despite the standards' simplicity, as long as higher-weighted assets tend to have higher risk then a positive relation between capital and risk will prevail, if the regulatory requirements are binding.
To expand its business or to take on additional risk, a bank would need to raise capital concurrently or beforehand to meet prudential requirements if it is currently constrained by them, or if it expects business expansion to absorb capital held above the regulatory minimum. Causation may run in the opposite direction, and be asymmetric, if regulators force banks to raise capital in response to increases in asset risk but do not require reductions in capital if asset risk falls.
To the extent that the regulatory risk weights reflect the true risks arising from banks' assets, a positive relationship between banks' asset volatility and capital-asset ratios is expected. However, changes in regulations concerning required capital may induce changes in the composition of portfolios, creating second-round effects on asset volatility – hence, the overall impact may be uncertain.
Kim and Santomero (1988) demonstrate, using a mean-variance utility maximisation framework, that an increase in flat-rate capital requirements may cause banks to choose higher-risk portfolios. Capital requirements restrict the opportunity set available to banks, prohibiting them from selecting certain asset portfolios on their efficient frontier. Although an increase in capital requirements limits choice even further, banks may still choose a higher-risk portfolio as they maximise utility along the new frontier. Whether this is the case depends on the bank's attitude towards risk; the stronger is the bank's appetite for risk, the more likely it becomes.
In the presence of a flat-rate capital regime, it is argued that, among banks that operate at or near the regulatory minimum capital levels, a positive relationship between capital and asset risk will result. In other words, banks which experience a regulatory induced increase in capital may substitute asset risk for leverage and, in doing so, circumvent the intent of the regulation. Basing capital standards on true asset risk mitigates the likelihood of this happening. Kim and Santomero derive optimal risk weights and show that their model places an upper bound on insolvency risk.
Keeley and Furlong (1990) object to using the mean-variance utility maximisation framework because it misrepresents the banks' efficient frontier by assuming that changes in the probability of bank failure do not affect the cost of deposits. They argue that, even for insured banks, borrowing costs are not impervious to changes in insolvency risk and, therefore, leverage. The reason is that, as explained in Section 2, a fixed-rate deposit insurance guarantee represents an option to the bank to sell its assets to the insuring agency at a strike price equal to the maturity value of its liabilities. The value of this option (per dollar of deposits) is an increasing function of both leverage and asset risk.[23] This relationship, in effect, lowers the expected marginal cost of deposits in the face of an increase in the probability of failure. Thus, Keeley and Furlong argue that, for the constant borrowing cost assumption to hold, the probability of failure must be zero; this, of course, contradicts the finding that an increase in capital requirements may increase insolvency risk. Keeley and Furlong conclude that once this oversight is corrected the results generated from such models no longer stand. Furlong and Keeley (1989) show, using both state-preference and options models, that an increase in required capital will not, by itself, cause a value-maximising bank to increase asset risk.
Before risk-based standards were introduced in 1988, established Australian banks were required to maintain a capital-asset ratio (not adjusted for risk) of 6.5 per cent.[24] Overall, Australian banks were well capitalised relative to the minimum regulatory requirements in the years surrounding the implementation of the new standards. Thus, it is arguable that regulatory capital requirements were not a strong force driving bank behaviour.
5.2 Agency Theory
Agency theories of the firm highlight the potential for conflicts of interest between equity holders and debt holders, and between equity holders and managers. The impact that this has on the capital structure decision is discussed in Jensen and Meckling (1976). Differences in motives between the various parties may also affect the relationship between risk and capital.
5.2.1 The asymmetry between debt and equity
(a) Debt market discipline
Higher levels of debt may encourage equity holders to demand riskier operations and investments. This can be best understood by viewing equity holders as having an option over the value of the firm (Equations (5) and (6)). The value of the option is a positive function of the volatility of the return on assets; because the option has a payoff structure with a lower bound of zero, as the return on assets becomes more variable, the expected payoff of the option at maturity also increases. Put more simply, if a risky investment proves successful the residual benefits will flow to equity holders, but if the investment fails, debt holders will fully absorb the losses. Knowing this, the debt holders (including depositors) demand higher compensating returns and/or restrictions on the activities of the firm (for example, covenants), thereby imposing agency costs on equity holders. One way for firms to reduce agency costs is to operate with lower leverage. Agency costs may, therefore, drive a positive relationship between risk and capital; if, for example, a bank takes on more risk, it may also decide to raise capital so as to appease debt holders who would otherwise impose additional agency costs on the bank.
In an environment where information asymmetries lead firms to use leverage as a signalling device, capitalisation and asset volatility may be complements rather than substitutes. For example, Leland and Pyle (1977) argue that a higher-quality firm (that is, one with low asset volatility) may signal that quality by increasing the capital-asset ratio. Since financial capital constitutes the bank's own stake in its risk management, it conveys a credible signal to debt holders of the resources allocated to ensuring the continued survival of the firm and thus the safety of depositors' claims. Signalling theory, therefore, predicts a negative cross-sectional correlation between the capital-asset ratio and asset volatility.
(b) Moral hazard
As discussed previously, many countries explicitly guarantee or insure bank deposits. Deposit insurance schemes have the common effect of making deposits risk-free in nominal terms. Deposit insurance, as a result, excludes depositors from the set of individuals who have a vested interest in the riskiness of the insured institution. Market signals may not, therefore, provide the necessary risk-reducing discipline to managers. It is argued that this gives banks an incentive to take on riskier activities without being adequately capitalised (see, for instance, Gennotte and Pyle (1991)).
Incentives for such risk taking are magnified in weak institutions by the policy of limited shareholder liability. Losses to equity holders are limited to the amount invested while there is no limit to earnings of equity holders if the project should prove successful. This leads to behaviour known as ‘betting the bank’, wherein the managers of the bank adopt a high-risk strategy which lowers the expected value of the bank, but which has a chance of yielding high profits. This behaviour is expected to be most prevalent amongst banks having negligible opportunities for profitable growth over time. A decline in a bank's capital-asset ratio is liable to increase the likelihood of moral hazard driven behaviour; thus, a negative relation between capital and asset risk is predicted by the moral-hazard theory.
However, even with extensive deposit guarantees, banks do not hold zero capital and take on infinite asset risk. One reason for this is that the bank's ability to raise funds from uninsured sources will continue to be influenced by its probability of failure. Whether there is a positive or negative relation between asset risk and capital depends on the marginal benefits and costs of asset risk and leverage.
5.2.2 Managerial risk aversion
The relationship between shareholders and the manager of a bank can also be affected by agency problems. Managers may have an incentive to decrease risk below the level desired by shareholders, since they have more to lose if the bank fails – managers have firm- and industry-specific human capital whereas shareholders generally have a smaller proportion of their wealth invested in the bank. Hence, risk-averse managers may seek to offset increases in asset risk with higher levels of capital, providing a further rationale for a positive relationship between asset risk and capital.
Regulatory capital constraints excepted, the theories outlined above do not make any predictions concerning the temporal ordering of movements in leverage and asset volatility. Transaction costs and variations in the degree of information asymmetry, between bank insiders and outsiders, dictate that capital issues are usually made in relatively large discrete steps. This leads us to expect that increases in capital would precede increases in asset risk. Reductions in capital, however, may more closely approximate a continuous process. In such a case, the relationship between the capital-asset ratio and asset volatility may be asymmetric: increases in capital preceding increases in asset volatility, and decreases in capital lagging or coinciding with asset-volatility declines.
Having outlined the theoretical framework within which we can consider the relationship between risk and capital, the following section presents the results of our analysis.
5.3 The Empirical Relationship Between Asset Volatility and Capital
The contingent-claim model assumes that the stock market is always efficient, but there are grounds for considering the crash to be an anomalous event that should be excluded from the analysis. Therefore, the months affected by the 1987 stock market crash are excluded from the empirical work presented in this section.
Statistical analysis of the data suggests that while asset volatility is stationary, for around half of the banks, the capital-asset ratio is integrated of order one.[25] The implications of this are two-fold. Firstly, our modelling needs to consider the relationship between the level of asset volatility and both the level of and month-to-month changes in the capital-asset ratio.[26] Secondly, the inferences drawn from our modelling are confined to the short-run dynamics of the relation rather than any longer-run behaviour.
5.3.1 Simple regression analysis
We first consider the contemporaneous correlation between the capital-asset ratio and asset volatility. Table 3 presents the correlation of asset volatility with the level and changes in the capital-asset ratio calculated across time for each bank. Asset volatility is found to have a strong positive relationship with the capital-asset ratio (the apparent non-stationarity of the capital-asset ratio places a strong caveat on this result). For all banks the correlation coefficient is positive, and for 12 out of the 15 banks the coefficient is significant at the 1 per cent level. When changes in the capital-asset ratio are considered a positive relation is found for most banks; the correlation, however, is significant for only four of the banks.
| Bank | Correlation between kt and σAt | Correlation between Δkt and σAt |
|---|---|---|
| A | 0.875*** | 0.284*** |
| B | 0.664*** | 0.098 |
| C | 0.854*** | −0.160 |
| D | 0.828*** | 0.098 |
| E | 0.172 | 0.273*** |
| F | 0.447*** | −0.143 |
| G | 0.497*** | 0.541*** |
| H | 0.813*** | 0.086 |
| I | 0.402*** | 0.229 |
| J | 0.134* | 0.108 |
| K | 0.597*** | 0.353*** |
| L | 0.092 | −0.152 |
| M | 0.917*** | 0.217* |
| N | 0.476*** | 0.146 |
| O | 0.546*** | 0.166 |
|
Notes: ***, * denote significance at the 1 and 10 per cent levels
respectively. Δkt is the month-to-month change in the capital-asset ratio. kt and σAt are obtained from the Case III paramaterisation of the model using historical estimates of σE. |
||
Figure 8 summarises the results of cross-sectional correlations for each month between March 1983 and April 1998. The black line shows the correlation between asset volatility and the level of the capital-asset ratio, while the grey line shows the correlation coefficient when the change in the capital-asset ratio is used. The small number of banks in this study (15) suggests a degree of caution in interpreting the results. Keeping this in mind, there is a consistently positive correlation between the capital-asset ratio and asset volatility (this correlation is significant about 75 per cent of the time). The cross-sectional correlation between the change in the capital-asset ratio and asset volatility tends to be close to zero, being significantly positive on only one fifth of occasions.
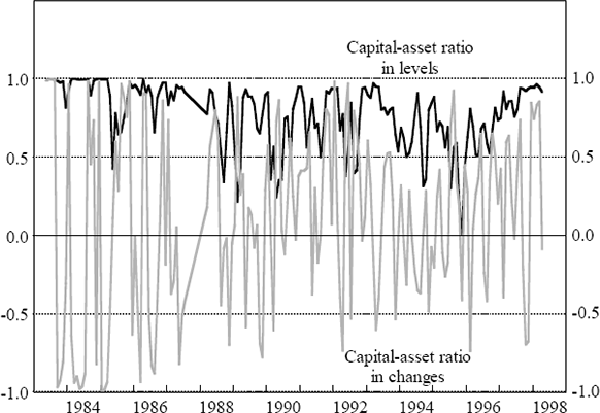
Our finding of positive correlation conflicts with models of moral hazard, which predict that as the capital-asset ratio falls banks are likely to take on riskier assets. Our results also contrast with the majority of studies in the US (see, for example, Benston and Kaufman (1998)). Australian banks' behaviour seems to more strongly reflect regulatory requirements, debt-market discipline and agency cost considerations.
5.3.2 Granger-causality tests
Since we have a panel of cross-sectional data with many more observations through time than across banks, our first step was to consider a seemingly unrelated regressions model. However, we failed to find evidence of significant contemporaneous correlation between disturbances from equations estimated separately for each bank. Hence, the results presented here are based on applying ordinary least squares to each bank's equation separately. These results are presented in Tables 4 and 5. Where significant, a trend or a broken trend (split between March 1983 – December 1991 and January 1992 – April 1998) is included in the model of asset volatility. In each equation, lags of the change in capital and the level of volatility are included as explanatory variables. Tables 4 and 5 present the number of lags included in each equation (chosen by eliminating insignificant lagged coefficients), the sum of the coefficients on the lagged variables and, in parentheses, the significance from testing whether all lagged variables can be excluded from the equation. The final two columns of Table 5 summarise impulse response functions for the two estimated equations considered together. The change in capital growth observed six months after a one standard deviation, one period, shock to asset volatility is shown for each bank. Similarly, the response of asset volatility to a temporary shock to capital growth is presented.
| Bank | Constant | Change in capital | Asset volatility | ||
|---|---|---|---|---|---|
| No. of lags | Sum of coefficients | No. of lags | Sum of coefficients | ||
| A | 0.000 (0.332) |
1 | 0.153 (0.154) |
1 | 0.015 (0.742) |
| B | 0.006 (0.004)*** |
6 | 0.394 (0.009)*** |
1 | −0.391 (0.016)** |
| C | 0.011 (0.069)* |
1 | 0.347 (0.022)** |
1 | −0.377 (0.070)* |
| D | 0.001 (0.021)** |
1 | 0.176 (0.004)*** |
1 | −0.047 (0.187) |
| E | 0.002 (0.246) |
1 | 0.028 (0.814) |
1 | −0.095 (0.206) |
| G | −0.001 (0.330) |
1 | 0.083 (0.414) |
7 | −0.016 (0.000)*** |
| H | 0.001 (0.420) |
1 | 0.183 (0.044)** |
1 | −0.015 (0.786) |
| I | 0.000 (0.975) |
4 | −0.479 (0.001)*** |
5 | 0.007 (0.040)** |
| J | 0.000 (0.998) |
1 | 0.093 (0.225) |
1 | −0.014 (0.738) |
| K | 0.006 (0.002)*** |
3 | 0.386 (0.001)*** |
9 | −0.275 (0.025)** |
| L | 0.001 (0.019)** |
1 | 0.054 (0.698) |
2 | 0.128 (0.003)*** |
| M | 0.000 (0.751) |
1 | 0.310 (0.000)*** |
1 | −0.067 (0.104)** |
| N | 0.007 (0.048)** |
9 | 0.039 (0.088)* |
2 | −0.337 (0.101) |
| O | −0.004 (0.098)* |
1 | 0.037 (0.795) |
9 | −0.184 (0.000)*** |
|
Notes: The numbers in parentheses show the significance level from testing
whether all lagged variables can be excluded from the regression. |
|||||
| Bank | Constant | Trend | Trend 1 | Trend 2 | Change in capital | Volatility | Impulse response | |||
|---|---|---|---|---|---|---|---|---|---|---|
| No. of lags |
Sum of Coefficients |
No. of lags |
Sum of Coefficients |
Change in capital (percentage points) | Asset volatility (percentage points) | |||||
| A | 0.000 (0.929) | 0.00004 (0.006)*** | 2 | −0.028 (0.089)* | 1 | 0.730 (0.000)*** | 0.003 | −0.008 | ||
| B | 0.003 (0.046)** | 5 | 0.554 (0.008)*** | 6 | 0.794 (0.000)*** | −0.005 | 0.188 | |||
| C | 0.035 (0.001)*** | 0.00026 (0.006)*** | 9 | 0.315 (0.004)*** | 2 | 0.440 (0.000)*** | 0.175 | 0.111 | ||
| D | 0.001 (0.105) | 0.00004 (0.007)*** | 1 | 0.166 (0.016)** | 1 | 0.709 (0.000)*** | −0.009 | 0.016 | ||
| E | 0.008 (0.001)*** | 1 | 0.156 (0.035)** | 1 | 0.575 (0.000)*** | −0.003 | 0.005 | |||
| G | 0.006 (0.000)*** | 1 | 0.023 (0.908) | 2 | 0.000 (0.604) | −0.300 | −0.001 | |||
| H | −0.006 (0.020)** | 0.00008 (0.004)*** | 1 | 0.207 (0.017)** | 1 | 0.588 (0.000)*** | −0.001 | 0.007 | ||
| I | −0.036 (0.005)*** | 0.00034 (0.000)*** | 4 | 0.667 (0.003)*** | 1 | 0.089 (0.614) | −0.176 | −0.056 | ||
| J | 0.026 (0.000)*** | −0.00006 (0.003)*** | 3 | 0.495 (0.018)** | 2 | 0.361 (0.000)*** | 0.002 | −0.050 | ||
| K | 0.018 (0.001)*** | −0.00010 (0.049)** | 0.00003 (0.389) | 7 | 0.890 (0.001)*** | 2 | 0.313 (0.000)*** | 0.057 | 0.133 | |
| L | 0.008 (0.001)*** | 1 | −0.062 (0.672) | 1 | 0.568 (0.000)*** | −0.004 | −0.002 | |||
| M | 0.000 (0.407) | 4 | 0.807 (0.028)** | 6 | 0.965 (0.000)*** | −0.012 | 0.131 | |||
| N | 0.002 (0.353) | 4 | 0.344 (0.156) | 6 | 0.929 (0.000)*** | −0.048 | 0.029 | |||
| O | −0.030 (0.043)** | 0.00029 (0.005)*** | 10 | 0.694 (0.001)*** | 4 | 0.139 (0.000)*** | 0.305 | 0.034 | ||
|
Notes: The numbers in parentheses show the significance level from testing
whether all lagged variables can be excluded from the regression. |
||||||||||
While there is variation across banks in the relation between asset volatility and capital, overall it can be seen that there is a significant two-way feedback relationship between the two variables. For most banks, increases in the growth of the capital-asset ratio precede an increase in asset volatility; banks build up their stock of capital in anticipation of expanding their risk exposures. The corollary to this is that reductions in the capital-asset ratio (for example, through capital buy-backs) presage a reduction in risk exposures (this is investigated further in Section 5.3.4). This finding is consistent with banks having to build up capital to avoid breaching regulatory requirements.
The results also suggest that an increase in asset volatility usually leads to a slowdown in the growth of the capital-asset ratio. To understand why this may occur requires us to add another layer of detail to the model presented in Section 2. Referring to Figure 1, each point on the distribution of assets represents the present value of a set of cash flows that may accrue from the assets. The moments of this distribution reflect those of the distributions pertaining to each cash flow. More specifically, the volatility of assets (i.e. the width of the distribution) reflects the uncertainty surrounding the cash flows, while the expected value of assets (i.e. the mean of the distribution) is equal to the present value of the expected cash flows. If the cash flows expected to accrue from the assets become more uncertain then the discount rate that is applied to the cash flows increases, causing their present value to fall – that is, the expected value of assets decreases. A further, and more obvious, effect is that the uncertainty surrounding the expected value of assets also increases. In terms of Figure 1, we can think of this as both a widening and a downward displacement of the distribution of assets. However, this displacement of the distribution is somewhat inconsistent with the model from which the results are derived. Recall that assets were assumed to follow Geometric Brownian Motion, which can be described by:
Our results suggest that an increase in the volatility of assets will reduce the market value of a bank's assets. For this displacement to occur, the drift term in Equation (14), μA, needs to be a function of σA; this is inconsistent with our assumption, made earlier, that the drift term is equal to zero. To some extent, this discrepancy can be rationalised by realising that we are assuming a zero drift over a short time horizon (one year), whereas the relationship detected by the Granger-causality tests is based on a much longer time period.
Thus, banks raise capital prior to expanding their risk positions, after which, some of that capital is effectively consumed by the risk exposures. The adjustment within this feedback system is quite quick. Scrutiny of the impulse response functions show that by six months the response in capital growth rates to a temporary shock in asset volatility has fully played out. The adjustment of asset volatility following a shock to capital growth is slower, taking around twelve months. The impulse response function results show that on average, across all banks, a one standard deviation, one period, increase in asset volatility leads to a slowdown in capital growth of 0.001 percentage points after six months, while an equivalent shock to capital growth yields a 0.04 percentage point increase in asset volatilities. That said, there is considerable variation across banks around these average responses.
5.3.3 The impact of the 1988 Capital Accord
For those banks with sufficient observations before and after 1988, we consider the extent to which the relationship between the capital-asset ratio and asset volatility may have altered following the introduction of the risk-based capital adequacy arrangements. We extend the models presented in Tables 4 and 5 by estimating separate coefficients on the inter-relationship for the periods March 1983 – December 1988 and January 1989 – April 1998. These results are presented in Appendix C.
The results support the notion that prior period increases in the level of asset volatility lead to a slow down in the growth of the capital-asset ratio. For most banks, there is a significant difference in the size of this effect following the introduction of the Capital Accord, with the magnitude of the impact of asset volatility on capital growth falling in most cases.
For most banks the magnitude of the effect that prior period changes in the capital-asset ratio have on the volatility of assets does not change significantly following the introduction of the Capital Accord. Whilst insignificant, the size of the effect does appear to have increased slightly. This could be interpreted as providing some weak evidence that the introduction of the Capital Accord strengthened the linkages between banks' risk taking and capital.
5.3.4 Is the relationship between capital and asset volatility asymmetric?
If regulators require banks to increase capital in response to increases in asset risk, but do not force reductions in capital if asset risk falls, then it is possible that the relation between capital and asset risk is asymmetric. The discrete nature of capital issues may also result in such asymmetry. Thus, the second modification that we make to our model is to differentiate between periods of growth and decline in the capital-asset ratio. The results are presented in Appendix C.
The impact of prior period volatility on growth in the capital-asset ratio is largely unaffected by whether capital growth was accelerating or slowing. As with the full sample results, increased prior period volatility tends to lead a slowdown in capital growth.
For half of the banks in our sample there is a significant difference in the effect of changes in the capital-asset ratio on volatility according to whether growth in the capital-asset ratio is positive or negative. Consistent with the full sample analysis, when the capital ratio is increasing there is a strong positive relation between previous growth in the capital-asset ratio and asset volatility. In contrast, when capital is declining the sign of the relationship is indeterminate (being positive for half of the banks and negative for the other half). Moreover, for most banks the relationship between the capital-asset ratio and asset volatility is weaker when capital growth is slowing. There does not seem to be any consistent relation between either the size of the bank or the bank's average capital-asset ratio and the size (and sign) of the coefficient.
These results are consistent with some asymmetry in supervisors' and markets' treatment of banks: while banks increase capital in advance of taking on risk exposures, falls in capital do not necessarily trigger reductions in asset volatility.
Footnotes
The results of our analysis suggest that this assumption is not a good one, with estimated asset volatility itself being quite variable. [22]
The option is valuable to shareholders because without it, they could be forced to raise the funds required to satisfy the debt holders. [23]
New entrants, primarily building societies converting to bank status and foreign banks taking up a banking licence in Australia, were required to adhere to a higher ratio. [24]
The order of integration of the capital ratio is a difficult statistical issue. Over the long run, theory would suggest that the capital-asset ratio is bounded since the risk of insolvency places a lower bound on the ratio and the need to provide shareholders with a competitive return caps the ratio. Over the 15 years included in our sample, however, the capital-asset ratio does not show any signs of reverting to some permanent or equilibrium level. [25]
Ordinarily, any relationship found from regressing an I(0) process on an I(1) process would be labelled spurious. However, because of the low power of these tests, we still report the results of regressions involving the level of the capital-asset ratio. [26]