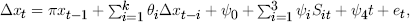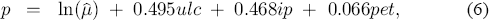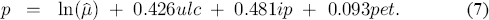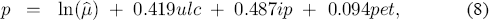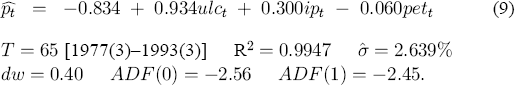RDP 9510: Modelling Inflation in Australia 4. Integration and Cointegration
November 1995
- Download the Paper 264KB
This section presents unit root tests for the variables of interest (Section 4.1). Then, Johansen's maximum likelihood procedure is applied to test for cointegration among the CPI, unit labour costs, import prices, and petrol prices (Section 4.2). Long-run price homogeneity and the adjustment mechanism are examined in the Johansen framework; and the estimated long-run elasticities are contrasted with those obtained by the Engle-Granger approach.
4.1 Integration
Before modelling the CPI, it is useful to determine the orders of integration for the variables considered. Table 1 lists fourth-order augmented Dickey-Fuller (1981) (ADF(4)) statistics for the CPI, unit labour costs, import prices, and petrol prices. Under standard optimizing behaviour, the mark-up itself should be stationary, so Table 1 also includes two constructed mark-ups, us and ud, which are derived from (18) and (19) below. The deviation from unity of the estimated largest root appears in parentheses below each Dickey-Fuller statistic: this deviation should be approximately zero if the series has a unit root. Unit root tests are given for the original variables (all in logs), for their changes, and for the changes of the changes. This permits testing whether a given series is I(0), I(1), I(2), or I(3), albeit in a pairwise fashion for adjacent orders of integration.[5]
| Null Order | Variable | |||||
|---|---|---|---|---|---|---|
| p | ulc | ip | pet | us | ud | |
| I(1) | 0.91 (0.02) |
−0.93 (−0.05) | −1.25 (−0.06) | −2.20 (−0.12) | −2.24 (−0.18) | −3.18 (−0.40) |
| I(2) | −3.01 (−0.44) | −3.77* (−1.00) | −2.55 (−0.68) | −4.04* (−1.56) | −2.86 (−0.95) | −3.38 (−1.05) |
| I(3) | −4.91** (−2.15) | −5.35** (−2.95) | −5.76** (−3.27) | −6.59** (−4.41) | −5.79** (−3.82) | −5.66* (−3.24) |
Notes
|
||||||
Empirically, all variables appear to be integrated of order two or lower. Unit labour costs and petrol prices appear to be I(1), whereas the CPI and import prices appear to be I(2) if inferences are made on the Dickey-Fuller statistics alone. However, the estimated roots for Δp and Δip are 0.56 (= 1 – 0.44) and 0.32 (= 1 – 0.68) respectively, which numerically are much less than unity. Thus, all four price series are treated below as if they are I(1), while recognizing that some caveats may apply. Specifically, it may be valuable to investigate the cointegration properties of the series, assuming that they may be I(2) (see Johansen (1992b, 1992c)), but doing so is beyond the scope of this paper.
4.2 Cointegration
Cointegration analysis helps clarify the long-run relationships between integrated variables. Johansen's (1988, 1991) procedure is maximum likelihood for finite-order vector autoregressions (VARs) and is easily calculated for such systems, so it is used here. Empirically, the lag order of the VAR is not known a priori, so some testing of lag order may be fruitful in order to ensure reasonable power of the Johansen procedure. Beginning with a fourth-order VAR in p, ulc, ip, and pet that includes a constant term and seasonal dummies, Table A1 in Appendix 2 shows that it is statistically acceptable to simplify to a first-order VAR.
Table 2 reports the standard statistics and estimates for Johansen's procedure applied to
this first-order VAR. The maximal eigenvalue and trace eigenvalue statistics (λmax
and λtrace) strongly reject the null of no cointegration in favour of
at least one cointegrating relationship, and little evidence exists for more than one. Parallel
statistics with a degrees-of-freedom adjustment (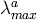 and
and 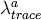 ) give a
similar picture, reflecting one very large eigenvalue (0.705) and three small eigenvalues.
) give a
similar picture, reflecting one very large eigenvalue (0.705) and three small eigenvalues.
| Eigenvalue | 0.705 | 0.138 | 0.125 | 0.058 | |
|---|---|---|---|---|---|
| Null hypothesis | r = 0 | r ≤ 1 | r ≤ 2 | r ≤ 3 | |
| λmax | 79.4** | 9.7 | 8.7 | 3.9* | |
 |
74.6** | 9.1 | 8.1 | 3.6 | |
| 95% critical value | 27.1 | 21.0 | 14.1 | 3.8 | |
| λtrace | 101.7** | 22.2 | 12.6 | 3.9* | |
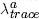 |
95.4** | 20.8 | 11.8 | 3.6 | |
| 95% critical value | 47.2 | 29.7 | 15.4 | 3.8 | |
| Standardized eigenvectors β′ | |||||
| Variable | p | ulc | ip | pet | |
| 1 | −0.495 | −0.468 | −0.066 | ||
| −0.830 | 1 | 0.242 | −0.206 | ||
| −2.578 | 1.538 | 1 | 0.575 | ||
| −2.603 | 4.835 | −3.727 | 1 | ||
| Standardized adjustment coefficients α | |||||
| p | −0.100 | −0.008 | −0.004 | 0.000 | |
| ulc | −0.061 | −0.201 | −0.016 | −0.002 | |
| ip | −0.075 | −0.011 | −0.010 | 0.017 | |
| pet | −0.096 | 0.156 | −0.140 | 0.002 | |
| Weak exogeneity test statistics | |||||
| Variable | p | ulc | ip | pet | {ulc, ip, pet} |
| χ2(·) | 63.1** | 1.89 | 1.34 | 0.43 | 3.45 |
| p-value | [0.00] | [0.17] | [0.25] | [0.51] | [0.33] |
| Multivariate statistics for testing stationarity | |||||
| Variable | p | ulc | ip | pet | |
| χ2(3) | 38.3** | 39.8** | 51.0** | 51.1** | |
| Statistics for testing the significance of a given variable | |||||
| Variable | p | ulc | ip | pet | |
| χ2(1) | 25.4** | 7.3** | 29.2** | 2.8 | |
Notes |
|||||
Table 2 also reports the standardized eigenvectors and adjustment coefficients, denoted β′ and α in a common notation. The first row of β′ is the estimated cointegrating vector, which can be written in the form of (2):
where a circumflex ˆ denotes an estimated or fitted value. All coefficients have their anticipated signs. Numerically, the coefficients on ulc and ip are approximately equal in value, reflecting the opposite and matching fluctuations of their real values in Figure 8. The sum of coefficients in (6) is close to unity (1.029), and statistically the restriction of long-run unit homogeneity cannot be rejected: χ2(1) = 0.61 [0.44]; see Johansen and Juselius (1990) for the form of the test. The asymptotic null distribution is denoted by χ2(·) with degrees of freedom in parentheses, and the asymptotic p-value is in square brackets. With long-run unit homogeneity imposed, (6) becomes:
Thus, the unit labour costs and import prices each have long-run elasticities of slightly less than one half, with petrol prices making up the remainder of about one tenth. The economic reasonability of these estimates is discussed in Section 6.
The coefficients in the first column of α measure the feedback effect of the (lagged) disequilibrium in the cointegrating relation onto the variables in the vector autoregression. Specifically, −0.100 is the estimated feedback coefficient for the CPI equation. The negative coefficient implies that an “excess” mark-up induces a lower CPI inflation rate. The coefficient's numerical value entails gradual adjustment to remaining disequilibrium and so substantial smoothing of unit labour costs, import prices, and petrol prices in obtaining the CPI.
The next row of Table 2 reports values of the statistic for testing weak exogeneity of a given variable for the cointegrating vector. Equivalently, the statistic tests whether or not the corresponding row of α is zero; see Johansen (1992a, 1992c). If it is zero, disequilibrium in the cointegrating relationship does not feed back onto that variable. Individually and jointly, unit labour costs, import prices, and petrol prices are weakly exogenous. Imposing weak exogeneity of unit labour costs, import prices, and petrol prices jointly with long-run homogeneity also is not rejected: χ2(4) = 4.99 [0.29]. The corresponding estimate of the cointegrating vector is:
and the feedback coefficient in the equation for p is −0.081. These estimates are virtually unchanged numerically from the unrestricted ones (Table 2) or from those obtained by imposing subsets of the hypotheses (e.g., as in (7)). The similarity of coefficient estimates across the various restrictions points to the robustness of the results and is partial evidence in favour of those restrictions. Weak exogeneity implies that the cointegrating vector and the feedback coefficients enter only the CPI equation, so inferences about those parameters can be conducted from a conditional model of the CPI alone without loss of information. Thus, weak exogeneity permits a much simpler modelling strategy, namely, a single equation analysis rather than a system one. Given the empirically acceptable restriction of weak exogeneity, Sections 5–7 pursue a single equation analysis of the CPI.
For comparison with (6), (7), and (8), Engle and Granger's (1987) test of cointegration obtains:
T, R2, 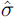 , and dw are the sample size of
the estimation period, the squared multiple correlation coefficient, the estimated equation
standard error, and the Durbin-Watson statistic respectively; the coefficients are estimated by
least squares; and the ADF statistics are calculated on the residuals from that static
regression, which includes seasonal dummies (not reported in (9)). Neither of the ADF statistics
is significant at MacKinnon's (1991) 90% critical level, paralleling the apparent unit roots
in Table 1 for the two constructed mark-ups, us and ud.
Even if cointegration is assumed, the co-efficient on pet in (9) has the wrong sign,
and long-run homogeneity does not appear to be satisfied, although formal testing is difficult,
given the complicated distribution of the coefficient estimates. These discrepancies between the
Johansen and Engle-Granger procedures may arise because the procedures treat dynamics
differently. Kremers, Ericsson and Dolado (1992) show analytically that the ADF test has low
power relative to Johansen and error correction-based procedures unless the dynamics of the
process satisfy a “common factor restriction”. That restriction is rejected for the
error correction model developed in the next section.[6]
, and dw are the sample size of
the estimation period, the squared multiple correlation coefficient, the estimated equation
standard error, and the Durbin-Watson statistic respectively; the coefficients are estimated by
least squares; and the ADF statistics are calculated on the residuals from that static
regression, which includes seasonal dummies (not reported in (9)). Neither of the ADF statistics
is significant at MacKinnon's (1991) 90% critical level, paralleling the apparent unit roots
in Table 1 for the two constructed mark-ups, us and ud.
Even if cointegration is assumed, the co-efficient on pet in (9) has the wrong sign,
and long-run homogeneity does not appear to be satisfied, although formal testing is difficult,
given the complicated distribution of the coefficient estimates. These discrepancies between the
Johansen and Engle-Granger procedures may arise because the procedures treat dynamics
differently. Kremers, Ericsson and Dolado (1992) show analytically that the ADF test has low
power relative to Johansen and error correction-based procedures unless the dynamics of the
process satisfy a “common factor restriction”. That restriction is rejected for the
error correction model developed in the next section.[6]
The penultimate row of Table 2 reports values of a multivariate statistic for testing the stationarity of a given variable. Specifically, this statistic tests the restriction that the cointegrating vector contains all zeros except for a unity corresponding to the designated variable, where the test is conditional on there being one cointegrating vector. For instance, the null hypothesis of a stationary CPI implies that the cointegrating vector is (1000)′. Empirically, all the stationarity tests reject with p-values less than 0.01%. By being multivariate, these statistics may have higher finite sample power than their univariate counterparts. Also, the null hypothesis is the stationarity of a given variable rather than the nonstationarity thereof, and stationarity may be a more appealing null hypothesis. That said, these rejections of stationarity are in line with the inability in Table 1 to reject the null hypothesis of a unit root in each of p, ulc, ip, and pet.
The final row of Table 2 reports chi-squared statistics for testing the significance of individual variables in the cointegrating vector. Each variable is significant except for petrol prices. The latter is retained in the single equation analysis below and appears to be statistically significant, perhaps from the additional restrictions on dynamics, including weak exogeneity.
Footnotes
For k ≥ 0, the notation I(k) indicates that a variable must be differenced k times to make it stationary. That is, if xt is I(k), then Δkxt is I(0). [5]
Kremers, Ericsson and Dolado (1992), de Brouwer, Ng and Subbaraman (1993), and Kamin and Ericsson (1993) find that invalid common factor restrictions markedly reduce the empirical power of the Engle-Granger procedure for detecting cointegration in money demand equations. Banerjee, Dolado, Hendry and Smith (1986) show that the static estimates may have large finite sample biases, which would explain the discrepancies between (9) and (6)–(8); see also Banerjee, Dolado, Galbraith and Hendry (1993). [6]