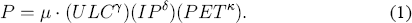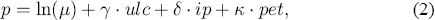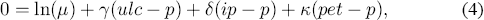RDP 9510: Modelling Inflation in Australia 2. A Conceptual Framework

While there are numerous theories and models of inflation, the enduring representation of the inflation process in Australia has been the mark-up model; see, for example, Richards and Stevens (1987). The mark-up model has a long-standing and continuing presence in economics generally; see Duesenberry (1950) and Franz and Gordon (1993) inter alia. The mark-up model is used throughout this paper, and it is general enough to embed several other well-known models, as noted below. This section describes the mark-up model underlying this paper's empirical analysis.

In the long run, the domestic general price level is a mark-up over total unit costs, including unit labour costs, import prices, and energy prices. Assuming linear homogeneity, the long-run relation of the domestic consumer price level to its determinants is:

The data are the underlying consumer price index (P), an index of the nominal cost of labour per unit of output (ULC), an index of tariff-adjusted import prices in domestic currency (IP), and an index of petrol prices in domestic currency (PET). The elasticities of the consumer price index with respect to ULC, IP, and PET are γ, δ, and κ, respectively, each of which is hypothesized to be greater than or equal to zero. The value μ – 1 is the retail mark-up over costs, and both the mark-up and costs may vary over the cycle.^[1]

In practice, (1) is expressed in its log-linear form:

where logarithms of variables are denoted by lower case letters. The log-linear form is used in the error correction model below. Linear homogeneity implies the following testable hypothesis:

which is unit homogeneity in all prices. Under that hypothesis, (2) can be rewritten as:

which links real prices in the labour, foreign goods, and energy markets. This representation will be particularly useful in interpreting the empirical error correction model in the context of multiple markets influencing prices; cf. Juselius (1992) and Metin (1994). Additionally, through the term (ip – p), (4) clarifies how the hypothesis of purchasing power parity is embedded in the mark-up model in (1). As discussed later, the empirical implementation also has ties to the Phillips curve by allowing the mark-up μ – 1 to depend upon the output gap.

Footnote

The nominal cost of capital per unit of output was also included in initial modelling of the CPI. However, no long- or short-run effects of unit capital costs on the CPI were found, so unit capital costs are excluded from discussion in the remainder of this paper. Appendix 1 describes the measure of unit capital costs used. [1]