Research Discussion Paper – RDP 2025-03 Fast Posterior Sampling in Tightly Identified SVARs Using ‘Soft’ Sign Restrictions
May 2025
1. Introduction
Sign-restricted structural vector autoregressions (SVARs) are used extensively by applied macroeconomists to estimate the effects of macroeconomic shocks. Researchers making use of sign restrictions typically work with the SVAR's ‘orthogonal reduced-form’ parameterisation and conduct Bayesian inference under a uniform prior on the orthonormal (or ‘rotation’) matrix, Q.[1] Posterior sampling in this setting is almost universally implemented using an accept-reject sampler; proposal draws are obtained from the posterior distribution of the reduced-form parameters and from a uniform distribution for Q, and are rejected if they do not satisfy the sign restrictions (e.g. Uhlig 2005; Rubio-Ramírez, Waggoner and Zha 2010; Arias, Rubio-Ramírez and Waggoner 2018).
Accept-reject sampling can be computationally burdensome when draws satisfy the sign restrictions with low probability, which occurs when the identifying restrictions substantially truncate the identified set for Q – that is, when identification is ‘tight’.[2] For example, Kilian and Murphy (2014) identify the effects of oil market shocks using sign restrictions on impulse responses augmented with bounds on the price elasticity of oil supply. Baumeister and Hamilton (2024) observe that 5 million draws of the parameters yield only 16 draws satisfying the identifying restrictions. In applications like this, obtaining a sufficiently large number of draws satisfying the identifying restrictions requires a very large number of proposal draws. The computational bottleneck associated with accept-reject sampling under tight identification is likely to become increasingly prominent, owing to a trend towards using richer sets of identifying restrictions (e.g. Inoue and Kilian 2024).
This paper develops an approach to sampling Q that mitigates the inefficiencies associated with brute force accept-reject sampling. The key feature of our approach is an initial sampling step based on ‘soft’ sign restrictions. This step yields draws of Q that do not necessarily satisfy the imposed sign restrictions, but allows the use of computationally efficient algorithms for sampling. Our approach involves: 1) specifying a target distribution that smoothly penalises parameter values that violate (or are close to violating) the sign restrictions; 2) using a Markov chain Monte Carlo (MCMC) algorithm – the slice sampler (e.g. Neal 2003) – to draw from this target distribution; and 3) applying an importance-sampling step to obtain draws from the desired distribution, which we take to be the uniform distribution over the identified set for Q given the (hard) sign restrictions. We emphasise that we do not consider conducting inference under the relaxed set of sign restrictions; the soft sign restrictions that we employ are only used to facilitate sampling from the posterior given the ‘hard’ sign restrictions. For an approach to conducting Bayesian inference under ‘non-dogmatic’ sign restrictions, see Baumeister and Hamilton (2018, 2019).
Our approach can lead to efficiency gains for two reasons. First, because we sample from a smooth density that tends to assign higher probability to parameter regions within the identified set, the sampler tends to move from its initial point towards the identified set. Second, once the sampler has moved to a parameter region within the identified set, it tends to stay there. The accept-reject sampler does not feature either of these behaviours, because candidate draws are independent.
Existing approaches to uniform sampling of Q under sign restrictions can in some cases be more efficient than accept-reject sampling, but are only applicable under particular classes of restrictions. Amir-Ahmadi and Drautzburg (2021) develop a Gibbs sampler that draws from a uniform distribution over the identified set for Q. However, the sampler is not applicable when the sign restrictions constrain all columns of Q (e.g. when there are restrictions on the impulse responses to all shocks) or when each restriction does not linearly constrain a single column of Q. Read (2022) extends this sampler to allow for zero restrictions.
Chan, Matthes and Yu (2025) leverage the fact that the uniform distribution for Q is preserved when permuting and/or flipping the signs of its columns, building on this idea to rapidly generate a large number of draws that satisfy restrictions on impact impulse responses. Their approach could be combined with a secondary accept-reject step to impose other restrictions. Of course, if the additional restrictions substantially tighten the identified set, an accept-reject step could be burdensome. Their approach is likely to be particularly helpful when the number of variables included in the SVAR is large; intuitively, permuting columns can be useful for generating many uniformly distributed draws of Q when there are many possible permutations. The gains from doing this are likely to be smaller in the settings that we consider, where the number of variables is relatively small.[3]
In contrast with existing approaches, our sampler can be directly applied when the identifying restrictions – potentially nonlinearly – constrain all columns of Q, and can thus handle a wide variety of identifying restrictions. These include restrictions on: impulse responses (e.g. Uhlig 2005); structural coefficients (e.g. Arias, Caldara and Rubio-Ramírez 2019); the magnitudes of structural elasticities (e.g. Kilian and Murphy 2012); long-run cumulative impulse responses (e.g. Furlanetto et al 2025); and forecast error variance decompositions (e.g. Volpicella 2022). They are also applicable under: shape or ‘ranking’ restrictions (e.g. Amir-Ahmadi and Drautzburg 2021); ‘narrative restrictions’ (e.g. Antolín-Díaz and Rubio-Ramírez 2018; Giacomini, Kitagawa and Read 2023); and restrictions on the relationship between ‘proxies’ and structural shocks (e.g. Arias, Rubio-Ramírez and Waggoner 2021; Giacomini, Kitagawa and Read 2022b; Braun and Brüggemann 2023).
Our approach could also be used to draw more efficiently from posterior distributions corresponding to non-uniform priors for Q. For example, the posterior sampler in Bruns and Piffer (2023) involves sampling from a uniform normal-inverse-Wishart posterior and using an importance sampler to draw from the posterior under a different prior, including priors specified directly over structural parameters, as in Baumeister and Hamilton (2015). This approach involves using accept-reject sampling to obtain draws of Q satisfying sign restrictions. Our algorithm could be embedded within their sampler to improve efficiency when identification is tight.
The inefficiency of accept-reject sampling can also be a bottleneck when using prior-robust Bayesian methods (e.g. Giacomini and Kitagawa 2021a; Giacomini, Kitagawa and Read forthcoming). In practice, implementing these methods requires calculating the bounds of the identified set for each parameter of interest (e.g. an impulse response) at every draw of the reduced-form parameters. One way to do this, as suggested in Giacomini and Kitagawa (2021a), is by obtaining many draws from a uniform distribution over the identified set for Q and computing the minimum and maximum of the parameter of interest over the draws. A large number of draws may be required to approximate identified sets with a high degree of accuracy (e.g. Montiel Olea and Nesbit 2021). Again, obtaining these draws via accept-reject sampling can be cumbersome when identification is tight.
The idea of ‘softening’ or smoothing out restrictions has been applied elsewhere. In the context of sampling, Souris, Bhattacharya and Pati (2019) develop a Gibbs sampler to draw from a smooth approximation of a truncated multivariate normal distribution subject to linear constraints. Our proposal also involves sampling from a smooth approximation of a truncated normal distribution, but the general set of constraints that we consider may be nonlinear. In the field of operations research, kernel smoothing methods have been employed when computing derivatives of simulated outcomes under processes where there are discontinuities in the sample path (e.g. Liu and Hong 2011; Bruins et al 2018).
We illustrate the utility of our approach in two main settings. First, we use a simple bivariate model to illustrate our approach and explore its efficiency relative to accept-reject sampling. We show that our approach performs favourably when the identified set for Q is assigned small measure under the uniform prior, which occurs when identification is tight. We also demonstrate that the approach continues to effectively sample from the target distribution when the identified set is made up of disconnected parameter regions.
Second, we revisit the model of the global oil market in Antolín-Díaz and Rubio-Ramírez (2018), which builds on Kilian (2009) and Kilian and Murphy (2012).[4] This model imposes a rich set of sign, elasticity and narrative restrictions, which simultaneously and nonlinearly constrain all columns of Q. We show that our approach is roughly an order of magnitude more efficient than accept-reject sampling in this application. Using the same model, we also illustrate the utility of our approach in conducting prior-robust Bayesian inference, which would be extremely computationally burdensome when implemented via accept-reject sampling. We find that inferences about the effects of shocks in the oil market obtained under this rich set of identifying restrictions are broadly robust to the choice of conditional prior for Q. Importantly, we argue that this apparent robustness is unlikely to be an artefact of numerical approximation error given the large number of draws used when approximating identified sets. We briefly outline an additional empirical application – a model of US monetary policy from Antolín-Díaz and Rubio-Ramírez (2018) – which demonstrates that the favourable performance of our sampler persists in a larger model.
The remainder of the paper is structured as follows. Section 2 describes the SVAR, outlines the identifying restrictions that can be imposed via our algorithm, and briefly explains standard and robust Bayesian approaches to inference in this setting. Section 3 describes accept-reject sampling and introduces our sampler based on soft sign restrictions. Section 4 illustrates our approach and explores its efficiency in a simple example. Section 5 applies the approach in an empirical setting. Section 6 concludes. The appendices contain proofs and additional details related to the empirical applications.
Notation. We use the following notation throughout the paper. ei,n is the ith column of the n×n identity matrix, In. 0n×m is an n×m matrix of zeros. For a n×m matrix X, vec(X) is the vectorisation operator, which stacks the elements of X into an nm×1 vector. If X is n×n, vech(X) is the half-vectorisation, which stacks the elements lying on or below the diagonal into an n(n+1)/2×1 vector. (.) is the indicator function.
2. Framework
This section describes the SVAR and its orthogonal reduced-form parameterisation, explains the range of identifying restrictions considered, and outlines the standard and robust Bayesian approaches to inference in this class of models.
2.1 SVAR and orthogonal reduced form
Let yt = (y1t,...,ynt)′ be an n×1 vector of random variables following the SVAR(p) process:
where A0 is an invertible n×n matrix with positive diagonal elements and . Conditional on past information, . The orthogonal reduced-form parameterisation is
where: are the reduced-form coefficients; is the lower-triangular Cholesky factor of the variance-covariance matrix of the reduced-form VAR innovations, with ut = yt – Bxt; and Q is an n×n orthonormal matrix. The reduced-form parameters are denoted by and the space of n×n orthonormal matrices by .
Impulse responses to standard deviation shocks can be obtained from the coefficients of the vector moving average representation:
where Ch is defined recursively by for with C0 = In. Element (i, j) of is the horizon-h impulse response of variable i to structural shock j, denoted by , where is row i of and is column j of Q.
2.2 Identifying restrictions
Imposing identifying restrictions on functions of the structural parameters is equivalent to imposing restrictions on Q, where the restrictions depend on .[5] Our algorithms allow for a wide variety of sign restrictions, including restrictions on:
- Impulse responses. The restriction is equivalent to , which is a linear inequality restriction on qj with coefficient vector that depends on . We also allow for ‘shape’ or ‘ranking’ restrictions on impulse responses (e.g. Amir-Ahmadi and Drautzburg 2021). An example is that for , which is equivalent to .
- Structural coefficients. A restriction on the matrix of contemporaneous structural coefficients is , which is equivalent to We can also consider restrictions on .
- Elasticities. Kilian and Murphy (2012) propose augmenting sign restrictions with restrictions on the magnitudes of particular elasticities, which they define as ratios of impulse responses. For example, a lower bound on the impact impulse response of variable i to a shock in the first variable that raises the first variable by one unit is , where is a known scalar. If the impulse response entering the denominator is restricted to be positive, we can equivalently represent this restriction as the linear inequality restriction . We can similarly allow for bounds on ratios of elements of .
- Functions of the structural shocks (‘narrative restrictions’). Narrative restrictions are inequality restrictions on functions of the structural shocks in specific periods (Antolín-Díaz and Rubio-Ramírez 2018; Ludvigson, Ma and Ng 2017, 2021; Giacomini et al 2023). For example, the restriction that shock j in period k was non-negative is . The restriction on the historical decomposition that shock j was the ‘most important contributor’ to the observed unexpected change in variable i between periods k and k+h is , where
- Similarly, the restriction that shock j was the ‘least important contributor’ to the observed unexpected change in variable i between periods k and k+h is .[6]
- Other restrictions. We can also allow for other types of inequality restrictions, including on long-run cumulative impulse responses (e.g. Furlanetto et al 2025), forecast error variance decompositions (e.g. Volpicella 2022), and the relationships between proxy variables and structural shocks (e.g. Arias et al 2021; Giacomini et al 2022b; Braun and Brüggemann 2023).[7] We do not detail these types of restrictions here, except to note that they can also be cast as (potentially nonlinear) inequality restrictions on Q.
As general notation, let represent a collection of s sign restrictions.[8] Given the sign restrictions, the identified set for Q is
The identified set collects observationally equivalent parameter values, which are parameters corresponding to the same value of the likelihood function (Rothenberg 1971). The identified set for Q induces identified sets for other parameters of interest, such as impulse responses. For example, the identified set for is .
2.3 Bayesian inference
The typical approach to conducting Bayesian inference in sign-restricted SVARs involves specifying a normal-inverse-Wishart prior for along with a uniform prior for Q (e.g. Uhlig 2005; Rubio-Ramírez et al 2010; Arias et al 2018; Inoue and Kilian 2024, 2025). The uniform prior for Q can be motivated by the fact that it assigns equal prior weight to observationally equivalent models or vectors of impulse responses (Arias et al 2025). As discussed below, it is also computationally convenient to obtain draws from a uniform distribution over .
In practice, obtaining draws from the resulting posterior for requires drawing from its normal-inverse-Wishart posterior and Q from a uniform distribution over , and rejecting draws of if they do not satisfy . As discussed in Uhlig (2017), this procedure implicitly assigns higher prior density – relative to the notional normal-inverse-Wishart prior – to values of corresponding to ‘larger’ identified sets. It therefore may be appealing to instead use a ‘conditionally uniform’ prior. The conditionally uniform prior also implies that the marginal likelihood is invariant to the choice of conditional prior for Q when the identified set is never empty (Amir-Ahmadi and Drautzburg 2021).
Given these considerations, we focus on the conditionally uniform prior and refer to the corresponding prior (and posterior) for as ‘conditionally uniform normal-inverse-Wishart’. Under this prior, draws from the posterior can be obtained by drawing from its normal-inverse-Wishart posterior, checking whether the identified set is non-empty and, if so, obtaining a fixed number of draws of Q from a uniform distribution over .
It is possible that is empty. When this is the case, the support of the reduced-form prior is implicitly truncated to parameter values such that is non-empty. It is possible to verify whether is non-empty under particular types of identifying restrictions before attempting to draw values of Q (e.g. Amir-Ahmadi and Drautzburg 2021; Giacomini, Kitagawa and Volpicella 2022; Read 2022). However, we are unaware of approaches to do this that are applicable under the wide class of sign restrictions that we consider. For the purposes of describing the sampling problem in Section 3, we assume that is non-empty. In Section 5, we describe how to handle the possibility that is empty in the context of the empirical application.
2.4 Robust Bayesian inference
Let be the prior for (truncated so is non-empty) and let be the conditionally uniform prior for Q, which is proportional to . After observing the data Y, the posterior for the joint parameter vector is , where is the posterior for . The prior is therefore updated by the data (via the likelihood), whereas the conditional prior is not. This implies that the posterior for may be sensitive to the choice of conditional prior, even asymptotically (e.g. Poirier 1998; Moon and Schorfheide 2012; Baumeister and Hamilton 2015).
Giacomini and Kitagawa (2021a) propose a prior-robust approach to Bayesian inference that eliminates this posterior sensitivity. Their approach can be used to quantify the degree to which posterior inferences are sensitive to the choice of conditional prior and to assess the informativeness of identifying restrictions. In some applications of set-identified SVARs, robust Bayesian methods have revealed that much of the apparent information in the standard Bayesian posterior is contributed by the conditional prior for Q (e.g. Giacomini and Kitagawa 2021a; Giacomini et al 2022b, 2023, forthcoming; Read forthcoming), though this is not necessarily always the case, particularly when rich sets of identifying restrictions are imposed (e.g. Inoue and Kilian 2024).
Conceptually, the prior-robust approach involves replacing with the class of all conditional priors that are consistent with the identifying restrictions, and summarising the corresponding class of posterior distributions. Practically, implementing this procedure requires computing the bounds of the identified set for each parameter of interest at each draw from the posterior for . Giacomini and Kitagawa (2021a) suggest approximating the bounds by obtaining many draws of Q from the uniform distribution over and computing the minimum and maximum of the parameter of interest over the draws.[9] A large number of draws may be required to approximate the identified set with a high degree of accuracy (e.g. Montiel Olea and Nesbit 2021).
In the empirical application (Section 5.3), we summarise the class of posteriors using the ‘set of posterior medians’ and a ‘robust credible interval’. The set of posterior medians is an interval with lower (upper) bound equal to the posterior median of the lower (upper) bound of the identified set; this interval contains all posterior medians that could be obtained given the class of priors consistent with the identifying restrictions. The -level robust credible interval is a robust Bayesian analogue of an equi-tailed Bayesian credible interval; it is an interval that is assigned at least posterior probability uniformly under any posterior in the class of posteriors.
3. Algorithms
This section describes algorithms that can be used to obtain draws of Q from the uniform distribution over . We focus on sampling from this component of the posterior (or prior) distribution rather than the joint distribution of , since the problem of sampling the reduced-form parameters is well understood (e.g. Del Negro and Schorfheide 2011). As a benchmark, we first describe an accept-reject algorithm. We then introduce our general approach to sampling based on ‘soft’ sign restrictions, before describing a specific MCMC sampler – the slice sampler – that can be used to implement our general approach.
3.1 Accept-reject sampling
The following algorithm describes an accept-reject sampler for drawing from the conditionally uniform distribution over .
Algorithm 1 (Accept-reject sampling). For a given value of :
Step 1. Draw an n×n matrix Z of independent standard normal random variables and let Z = be the QR decomposition of Z, where is orthonormal and R is upper-triangular with non-negative diagonal elements.
Step 2. Normalise the signs of the columns of such that and let Q be the normalised matrix. If , then
Step 3. Keep the draw if it satisfies and terminate the algorithm. Otherwise, return to Step 1.
Step 1 draws from a uniform distribution over using an algorithm proposed in Stewart (1980) (see also the descriptions in Rubio-Ramírez et al (2010) and Arias et al (2018)). Step 2 normalises the draw so that the sign normalisation diag is satisfied, which increases the efficiency of the sampler relative to a sampler that omits this step and uses the subsequent accept-reject step to impose the sign normalisation.[10] Step 3 is the accept-reject step, which simply involves checking whether the sign restrictions are satisfied. The algorithm is repeated to obtain the desired number of draws.
Let Q(Z) be a function that returns Q in the QR decomposition of Z (so Z = QR). Algorithm 1 can be interpreted as drawing Z from the truncated normal distribution with density
where fZ(Z) is the density of the standard matrix normal distribution. The interpretation of Algorithm 1 as drawing from this density will be useful in introducing our sampler.
The challenge with using accept-reject sampling in this setting is that it may take a large number of candidate draws (and thus computational time) to obtain a sufficiently large number of draws satisfying the identifying restrictions. This will occur when is assigned small measure under the uniform distribution over – that is, when identification is tight.
3.2 Soft sign restrictions
The indicator function appearing in Equation (7) can be decomposed into a product of indicator functions corresponding to individual sign restrictions:
where and represents the lth sign restriction with l = 1,...,s. The key feature underlying our approach is that we replace the indicator function with a smooth regularisation (or penalty) function , which satisfies the following assumption.
Assumption 1. The regularisation function is such that
In addition, for some finite K > 0, it satisfies
for all and .
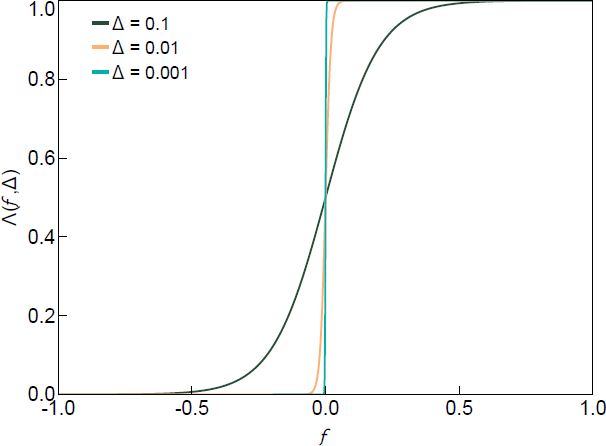
can be interpreted as a function that penalises draws of Q (equivalently, Z) that violate (or are close to violating) the sign restrictions by down-weighting their density. In the limit as , the regularisation function converges to the indicator function. One choice for that satisfies Assumption 1 (and that we will make use of below) is the logistic function:
This function is illustrated in Figure 1 for different values of .
We propose sampling from a smooth density that replaces the indicator function with the regularisation function:
The advantage of working with this smooth density is that alternative sampling algorithms, such as MCMC methods, can be directly applied, which obviates the need for accept-reject sampling. In the limit as , the probability of obtaining a draw violating the restrictions approaches zero and the draws of Q are approximately uniformly distributed over . This claim is formalised in the following proposition.
Proposition 1. Assume the conditions in Assumption 1 hold and let T : be such that . Then,
where and are expectations taken under f and , respectively.
For , the obtained draws of Z will not necessarily satisfy the sign restrictions and – conditional on satisfying the sign restrictions – will not follow the desired truncated normal distribution; equivalently, the draws of Q will not be uniformly distributed over . However, an importance-sampling step can be applied to obtain draws from an approximation of the desired distribution. The importance weights are given by
We can compute these importance weights up to a normalising constant simply by evaluating the regularisation function and checking whether the sign restrictions are satisfied. The normalising constant is the ratio of the probability measures assigned to the identified set under the two probability distributions, and is computationally costly to obtain. An implication of ignoring this normalising constant is that the importance sampler draws from a distribution that is not exactly equal to . However, a corollary of Proposition 1 is that the normalising constant converges to one as (almost surely under the reduced-form prior). This implies that any bias present in the importance sampler should be small for small enough choices of .
Theoretically, a smaller reduces the bias when approximating the posterior distribution of the structural parameters. However, a smaller also introduces sampling inefficiencies as the distribution becomes steeper (i.e. as the gradient of the log density function becomes larger). In the context of a random walk Metropolis algorithm, this steepness implies the need for a relatively smaller tuning parameter (i.e. the scale of the proposal distribution) to achieve a reasonable acceptance rate, as larger steps are more likely to be rejected in regions with high gradient changes. In the next section, we discuss an alternative method – slice sampling – that is more robust in such situations, offering improved efficiency in navigating steep target distributions.
Finally, if the draws of Q are used only to approximate the bounds of an identified set, such as when conducting prior-robust Bayesian inference, resampling the draws is unnecessary and it suffices to discard draws that violate the sign restrictions. This is because the approximated bounds depend only on the minimum and maximum values of the parameter of interest evaluated at the draws of Q, so the distribution of the draws over the identified set does not matter in this case.
3.3 Slice sampling
There are many MCMC methods that could be used to sample from . We make use of the slice sampler, motivated by its robust convergence properties, efficiency (relative to standard random walk Metropolis algorithms) and ease of implementation (Neal 2003).
The slice sampler is motivated by the fact that sampling from is equivalent to sampling uniformly from the region under the density function. The ‘simple’ slice sampler constructs a Markov chain that converges to this uniform distribution by alternating between two steps: 1) sample y uniformly from the interval given some predetermined Zk; and 2) sample Zk+1 uniformly from the ‘slice’ .[11] Iterating over this process generates a sequence of dependent draws from the target density. Figure 2 illustrates this idea in a univariate setting.
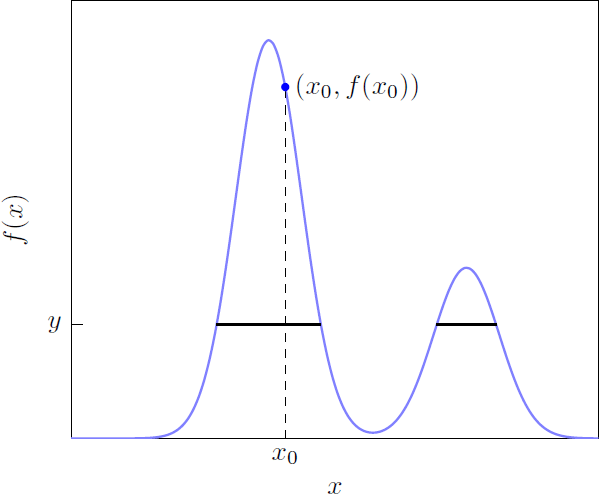
Notes: Given an initial value x0, y is a random draw from a uniform distribution on the interval [0, f (x0)] (the dashed vertical line). The solid black line represents the slice . A uniform draw is obtained from to update the initial value of x.
Mira and Tierney (2002) prove that if the target density is bounded and has support with finite Lebesgue measure, then the simple slice sampler is uniformly ergodic. More importantly, as noted by Roberts and Rosenthal (1999), the simple slice sampler is almost always geometrically ergodic, which is a property shared by very few other MCMC algorithms. These properties have led to slice sampling becoming a widely used method for sampling from non-standard distributions in low dimensions, although the applicability of the simple slice sampler is limited. In the multivariate setting, sampling uniformly from is generally infeasible, making the second step of the simple slice sampling algorithm impractical. To address this, the second step is typically modified to sample a Markov chain on , which maintains the uniform distribution over the slice as its invariant distribution.
In the multivariate setting, the slice sampler can be implemented by updating each variable in turn or all variables simultaneously. We build on Matlab's implementation of the slice sampler, which updates all variables simultaneously.[12] Sampling directly from a uniform distribution over the slice is infeasible in the current setting. However, as discussed above, any update that leaves the uniform distribution over the slice invariant will yield a Markov chain that converges to the target distribution. Matlab's implementation of the slice sampler updates the chain in a way that satisfies this condition using an approach described in Neal (2003). To briefly summarise, this procedure involves: randomly positioning a hypercube with side width w around the initial point; drawing a point from a uniform distribution over the hypercube; and repeatedly shrinking the hypercube (‘shrinking in’) if the candidate draw lies outside the slice until a draw is obtained within the slice.
To give an example of the shrinking-in procedure, consider the univariate setting illustrated in Figure 2. Let [xl, xr] be an interval of width w randomly positioned around x0. Consider a random draw x(p) from the uniform distribution over [xl, xr]. If , we set x1 = x(p). If , we shrink the interval by setting xl = x(p) if x(p) < x0 or xr = x(p) if x(p) > x0. We draw again from the uniform distribution over the updated interval, repeating this process until we obtain a draw within .
The choice of w will affect the speed at which the Markov chain converges to the target distribution and the sampler's computational efficiency. Under the general class of identifying restrictions we consider, there is no guarantee that is path connected, which means the smoothed density may be multimodal. A small value of w may lead to difficulties moving between modes and slow convergence. On the other hand, setting w too large can make the sampler computationally inefficient, because many shrinking-in steps may be required to obtain a draw that lies within the slice. We try to balance these considerations by using a ‘contaminated’ proposal, where w = 1 with 95 per cent probability and w = 3 with 5 per cent probability. Choices of w on this scale seem reasonable given that, for small values of ∆, the target distribution resembles a truncated multivariate standard normal distribution.
4. Numerical Illustration and Monte Carlo Experiments
This section illustrates how our method works and explores its efficiency relative to accept-reject sampling using a simple bivariate model as an example. This allows us to easily and transparently control the size of the identified set as well as visualise the performance of the algorithm. We first consider a case where the identified set is connected before illustrating the ability of our approach to navigate the more challenging circumstance where the identified set consists of disconnected parameter regions. We consider higher-dimensional models in the empirical applications (Section 5).
4.1 Connected identified set
Let yt = (pt, qt)′ contain log price and quantity, and consider imposing the following pattern of sign restrictions on the impulse responses:[13]
The restrictions imply that the first equation of the model can be interpreted as a supply curve and the second as a demand curve. The price elasticity of supply is .[14] Consider augmenting the sign restrictions with the elasticity restriction with .
Let vech and note that (2) can be represented as
where we leave it implicit that (e.g. Baumeister and Hamilton 2015).
It can be shown that the sign restrictions generate the following identified set for :
The upper bound of the identified set converges to zero as and to (i.e. the lower bound) as . The elasticity restriction therefore provides a convenient way to explore the efficiency of our algorithm relative to accept-reject sampling as the size of the identified set changes.
To illustrate the sampling approach in this setting, we fix and assume the goal is to draw from the uniform distribution over , which is equivalent to drawing from a uniform distribution over (Baumeister and Hamilton 2015). The accept-reject algorithm can be interpreted as drawing from a uniform distribution over the identified set given the sign normalisations only, and rejecting draws of that violate the sign restrictions.[15] In contrast, the slice sampler generates a Markov chain whose invariant distribution is the distribution over induced by . For , this distribution assigns positive density outside , so the slice sampler will return draws of outside of with positive probability, though draws of within will be sampled with higher probability. The resampling step then discards draws outside of and reweights the remaining draws so that the resulting distribution is (approximately) uniform.
Figure 3 illustrates the sampler under different values of .[16] When = 100 (top left panel), which we take to approximate the behaviour of the algorithm as , values of that violate the sign restrictions are essentially not penalised. The slice sampler therefore generates draws of Q from a uniform distribution over (2), which corresponds to being uniformly distributed over the interval . When (top right panel), values of that violate the sign restrictions have their density penalised, but a substantial proportion of draws obtained via slice sampling violate the sign restrictions. Values of that satisfy the sign restrictions but are close to the bounds of the identified set also have their density penalised, so the distribution of draws satisfying the sign restrictions is not uniform. Decreasing (bottom two panels) more strongly penalises values of that violate the sign restrictions, so a far smaller proportion of draws violate the restrictions, and the effective sample size following importance sampling is much larger. Following importance sampling, the draws are approximately uniformly distributed over .
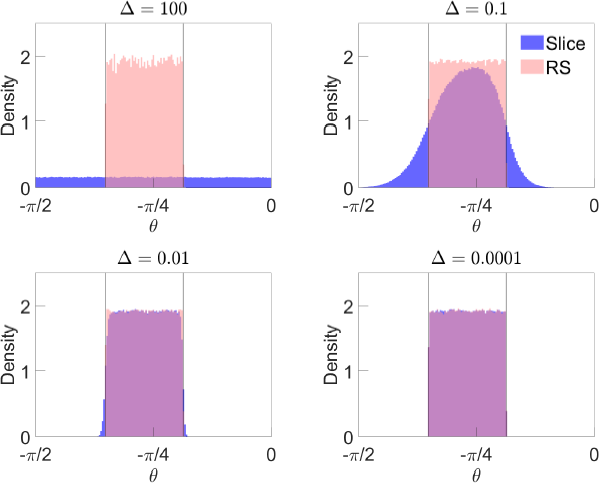
Notes: ‘Slice’ is distribution of draws obtained using slice sampler before resampling using importance weights; ‘RS’ is distribution after resampling. Vertical lines represent bounds of identified set. Parameter values are and . Based on one million draws.
To examine the computational efficiency of the sampling algorithms in this setting, we obtain 10,000 draws from in each of 100 replications where the slice sampler is initialised at a different randomly generated value. We compute the average time taken to obtain the draws and the average effective sample size. If wk is the importance weight attached to the kth draw, the effective sample size (expressed as a percentage of the original number of draws) is To illustrate the trade-off between speed and effective sample size, we consider values of {0.1,0.01,0.001,0.0001} and {1,0.1,0.01} (Table 1).[17]
| Algorithm | Speed (seconds) | Effective sample size (%) | |||||
|---|---|---|---|---|---|---|---|
| = 1 | = 0.1 | = 0.01 | = 1 | = 0.1 | = 0.01 | ||
| Accept-reject | 0.19 | 1.27 | 12.19 | 100.00 | 100.00 | 100.00 | |
| = 0.1 | 0.49 | 0.49 | 0.47 | 78.41 | 21.33 | 2.27 | |
| = 0.01 | 0.52 | 0.76 | 0.86 | 97.20 | 81.20 | 21.48 | |
| = 0.001 | 0.51 | 0.79 | 1.26 | 99.36 | 97.45 | 81.19 | |
| = 0.0001 | 0.51 | 0.78 | 1.25 | 99.25 | 98.12 | 96.78 | |
|
Notes: Averages based on 100 Monte Carlo replications with 10,000 draws of Q. controls width of identified set. controls penalisation of parameter values that violate (or are close to violating) sign restrictions in slice sampler. |
|||||||
When is relatively large, so that the identified set is ‘wide’, accept-reject sampling is more efficient than our approach, generating more effective draws in less time. As decreases and the size of the identified set shrinks, the computational efficiency of our approach increases relative to accept-reject. For example, when = 0.01, on average it takes 12.2 seconds to generate 10,000 draws using accept-reject, whereas the slice sampler with = 0.0001 generates around 9,700 effective draws in 1.3 seconds. For a given value of , increasing tends to increase computing time but also the effective sample size, since fewer candidate draws violate the sign restrictions.
4.2 Disconnected identified set
In general, may be made up of disconnected regions. Sampling from a distribution that is supported on disconnected parameter regions can pose challenges for MCMC algorithms, because the Markov chain may become ‘stuck’ in one region and not adequately traverse the target distribution. In contrast, by virtue of its independent proposal density, the accept-reject algorithm does not suffer from this problem. In this exercise, we illustrate our sampling approach in a setting where the identified set is disconnected.
Consider imposing the restriction that the impulse response of the first variable to the second shock is weakly greater than some positive scalar: for (when at any value of ). All other impulse responses are unrestricted and we continue to impose the sign normalisation . This example nests Example B.5 in Giacomini and Kitagawa (2021b) when . When , the restrictions generate the following identified set for :
which is the union of two disconnected intervals.[18] For a given value of , the total length of the identified set shrinks with increasing . This example therefore provides a simple setting to illustrate our sampler when the identified set is disconnected.
Figure 4 illustrates the sampler under different values of . Even at small values of , the sampler continues to cover the identified set – and thus generate draws from the target distribution – despite the identified set being disconnected. In the case where = 0.0001, 55.4 per cent of draws lie within the first interval, which is close to the theoretical probability under the uniform distriution (55.7 per cent). Our sampler therefore appears to adequately mix across the two regions.
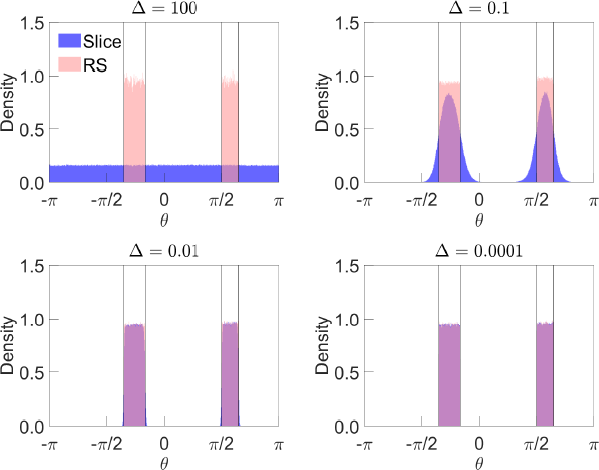
Notes: ‘Slice’ is distribution of draws obtained using slice sampler before resampling using importance weights; ‘RS’ is distribution after resampling. Vertical lines represent bounds of identified set. Parameter values are and = 0.5. Based on one million draws.
These results point to the potential for our approach to improve the computational efficiency of posterior sampling under sign restrictions when the restrictions substantially truncate the identified set, even in cases where the identified set is disconnected. To assess whether the approach can deliver on this promise, in the next section we turn to a realistic empirical application.
5. Empirical Application: Demand and Supply Shocks in the Oil Market
To explore the performance of the algorithms in an empirical setting, we consider the model of the global oil market in Antolín-Díaz and Rubio-Ramírez (2018), which builds on Kilian (2009) and Kilian and Murphy (2012). We select this application because it involves a rich set of identifying restrictions – sign restrictions, elasticity restrictions and narrative restrictions – that (nonlinearly) constrains all columns of Q. It is therefore a useful setting in which to illustrate the broad applicability of our sampling approach. We compare the performance of our approach against accept-reject sampling when conducting standard Bayesian inference under the usual uniform prior. We also demonstrate the utility of our approach when conducting prior-robust Bayesian inference, including by using robust Bayesian methods to quantify the importance of different narrative restrictions in driving inferences about the effects of oil market shocks.
5.1 Model and identifying restrictions
The model's endogenous variables are an index of real economic activity (REAt), the growth rate of global oil production (PRODt) and the log of the real price of oil (RPOt). The VAR includes 24 lags and a constant, and is estimated on monthly data from January 1971 to December 2015.[19] The reduced-form prior is a diffuse normal-inverse-Wishart distribution, so the posterior is also normal-inverse-Wishart (e.g. Del Negro and Schorfheide 2011).
Let yt = (REAt, PRODt, RPOt)′. The following sign restrictions are imposed on the impact impulse responses:
These restrictions imply that the model's three structural shocks can be interpreted as shocks to aggregate demand, oil-specific demand and oil supply, respectively. Each of these sign restrictions can be written as a linear inequality restriction on a single column of Q.
The ‘price elasticity of oil supply’ is restricted to be less than 0.0258, which Kilian and Murphy (2012) argue is a credible upper bound based on existing evidence. This elasticity is defined as the ratio of the impact response of production growth to the impact response of the real price of oil following aggregate demand or oil-specific demand shocks, so the restrictions are:[20]
The narrative restrictions include restrictions on the signs of the structural shocks in specific periods (‘shock-sign restrictions’), as well as their contributions to one-step-ahead forecast errors (i.e. historical decompositions). The shock-sign restrictions are that the oil supply shock was non-negative in December 1978, January 1979, September 1980, October 1980, August 1990, December 2002, March 2003 and February 2011, which are months in which narrative accounts suggest that there were unexpected disruptions in oil production.[21] These restrictions require that
for values of t corresponding to the dates listed above. Each of these restrictions is a linear inequality restriction on a single column of Q. The restrictions on the historical decomposition include the restriction that the oil supply shock was the ‘most important contributor’ to the observed unexpected movement in oil production growth in these months. This requires that . Finally, for the periods September 1980, October 1980 and August 1990, aggregate demand shocks are restricted to be the ‘least important contributor’ to the unexpected movement in the real price of oil, which requires that . These are nonlinear restrictions that simultaneously constrain all columns of Q.[22]
5.2 Standard Bayesian inference
The goal of our first exercise is to obtain 1,000 draws of from its posterior (such that the identified set is non-empty) and 1,000 draws of Q from the uniform distribution over at each draw of , yielding 106 draws of the impulse responses given the conditionally uniform normal-inverse-Wishart prior. We do this using the accept-reject sampler and our approach based on soft sign restrictions and the slice sampler.
As noted in Section 2.3, the identified set may be empty. When using the accept-reject sampler, we make 1,000 unsuccessful attempts to draw Q before approximating as empty and redrawing . When using the slice sampler, if none of the 1,000 draws of Q satisfy the identifying restrictions, we redraw . Similar computational effort is therefore used to determine whether the identified set is non-empty under both approaches.
At each draw of , we find an initial value for the slice sampler by using a numerical optimisation routine to find a (potentially local) maximum of the log target density with = 0.1; experiments suggest that this initialisation strategy increases the efficiency of the sampler relative to initialising at a random draw.[23] We set = 10–5 when sampling and examine alternative choices below.
Figure 5 summarises the posterior distributions of the impulse responses obtained using the two samplers. The results are very similar.[24] The accept-reject sampler takes around 80 hours to generate the desired number of draws from the posterior, whereas the slice sampler takes only 3.8 hours. The effective sample size (as a percentage of the original sample size) from the slice sampler is around 82 per cent. To adjust for the difference in effective sample size, we compare the number of effective draws per hour, which is the effective sample size divided by the number of hours taken to obtain the draws. The accept-reject sampler generates approximately 12,400 draws per hour, whereas the slice sampler generates around 210,000 effective draws per hour. On this basis, our approach is an order of magnitude more computationally efficient than accept-reject sampling, generating around 17 times as many effective draws per unit of time.
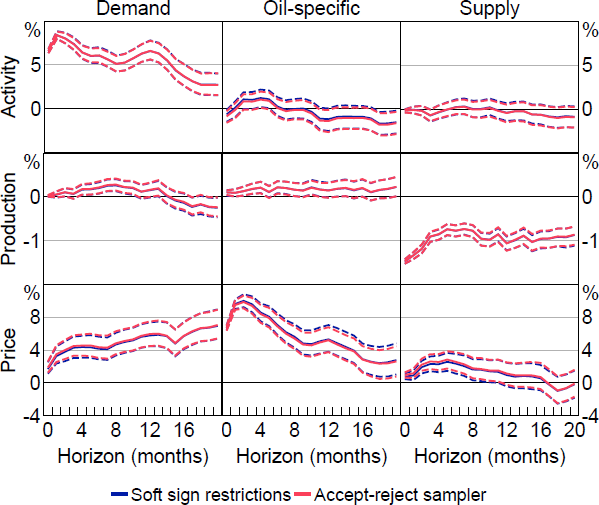
Note: Solid lines are posterior medians and dashed lines are 68 per cent credible intervals.
Figure 5 suggests that the posterior distributions of the impulse responses generated by the samplers are similar. However, as discussed in Section 3.2, our approach samples from an approximation of the uniform distribution over , where the approximation error vanishes as . We can examine the magnitude of the approximation error by comparing the distributions of the draws obtained using the two samplers at a fixed value of . Using a random draw of from its posterior, quantile-quantile plots and two-sample Kolmogorov-Smirnov test statistics suggest that, while some differences in distributions are apparent across the two samplers, the differences tend to be quantitatively small. These quantitatively small differences appear to largely wash out when averaging over (noting that our algorithm is better able to determine whether the identified set is non-empty, which will also generates differences in the approximated posterior distributions, as discussed in Section 5.4 below).
The results in this section have been obtained with the penalisation parameter set to 10–5. However, does not have a natural scale, so the choice of this parameter is somewhat arbitrary. Table 2 compares the computational performance of our sampler at different choices of . For all values of considered, our sampler generates more effective draws per hour than the accept-reject sampler. Effective draws per hour are maximised at = 10–3 and decline slowly as increases. Choosing small values of to mitigate bias is therefore feasible without large sacrifices in terms of computational efficiency.
| Algorithm | Speed (hours) | Effective draws per hour (′000) |
|---|---|---|
| Accept-reject | 77.0 | 13 |
| Soft sign restrictions: | ||
| = 10–1 | 1.4 | 36 |
| = 10–2 | 2.1 | 167 |
| = 10–3 | 2.8 | 254 |
| = 10–4 | 3.4 | 234 |
| = 10–5 | 3.8 | 209 |
| = 10–6 | 4.4 | 184 |
|
Notes: controls penalisation of parameter values that violate (or are close to violating) sign restrictions in slice sampler. Effective draws per hour rounded to nearest thousand. |
||
5.3 Robust Bayesian inference
Our second empirical exercise exploits our sampling approach to implement the prior-robust Bayesian inferential procedure proposed in Giacomini and Kitagawa (2021a). Following an algorithm proposed in Giacomini and Kitagawa, we approximate the bounds of the identified set for each impulse response by computing the minimum and maximum of over a large number of draws from . These approximations will possess error that will vanish as the number of draws of Q goes to infinity. An important consideration when using this approach is therefore the number of draws of Q used to approximate the bounds.
Montiel Olea and Nesbit (2021) derive results about the number of draws required to approximate identified sets up to a desired degree of accuracy. Based on their results, if we want to guarantee a misclassification error less than 5 per cent with probability at least 95 per cent, we require over 20,000 draws from at each draw of . From the exercise in Section 5.2, it is clear that implementing the robust Bayesian approach to inference with this target level of accuracy would be extremely computationally costly. We therefore turn to our algorithms based on soft sign restrictions. See Appendix B.1.1 for details about how we implement our approach in this exercise.
5.3.1 Assessing prior sensitivity
Figure 6 plots the set of posterior medians and 68 per cent robust credible intervals for the impulse responses, which are summaries of the class of posteriors obtained under the prior-robust Bayesian procedure (see Section 2.4). These quantities can be used to assess the influence of the conditional prior on the posterior; intuitively, if the set of posterior medians is ‘wide’ and/or the robust credible intervals are substantially wider than the standard credible intervals, the conditional prior contributes a lot of the apparent information in the posterior, and posterior inferences may be sensitive to the choice of conditional prior. For comparison, Figure 6 also plots the posterior median and 68 per cent credible interval obtained under the standard Bayesian approach to inference with a conditionally uniform prior for Q.
The influence of the conditional prior on the posterior varies somewhat across different impulse responses. For the oil supply shock, the set of posterior medians tends to be narrow, and the robust credible intervals are similar in width to the standard credible intervals. In other words, the responses to an oil supply shock are tightly identified and the conditional prior has little influence on posterior inferences about these responses. For demand-side shocks, the influence of the conditional prior is more noticeable in some cases, particularly for the response of oil prices and the response of activity to an oil-specific demand shock. This indicates that these responses are less tightly identified and the conditional prior contributes more of the apparent information in the posterior.[25] Nevertheless, even in these cases, the robust credible intervals tend to exclude zero in the same cases where the standard credible intervals exclude zero. Overall, this suggests that inferences about the effects of shocks in the oil market obtained under this rich set of identifying restrictions are not particularly sensitive to the choice of conditional prior for Q.
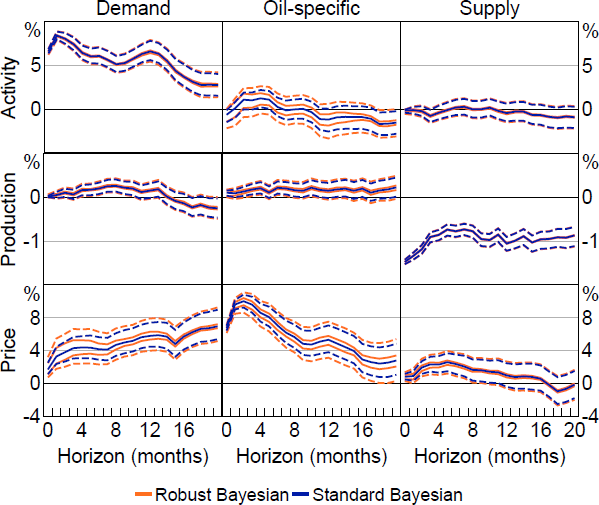
Notes: Solid lines are (sets of) posterior medians and dashed lines are 68 per cent (robust) credible intervals. Results obtained using soft sign restrictions.
Importantly, the large number of draws of Q used to approximate the identified set and the guarantee on approximation accuracy from Montiel Olea and Nesbit (2021) mean that this apparent robustness to the choice of conditional prior is unlikely to be an artefact of approximation error. These results complement exercises in Inoue and Kilian (2024), who highlight applications where posterior inferences do not appear to be driven by the uniform prior for Q.
5.3.2 Assessing the importance of the narrative restrictions
Antolín-Díaz and Rubio-Ramírez (2018) show that their results can largely be replicated by replacing the set of narrative restrictions with a single narrative restriction. In particular, alongside the sign and elasticity restrictions, they consider imposing the narrative restriction that aggregate demand shocks were the least important contributor to the unexpected movement in the real price of oil in August 1990 (corresponding to the start of the Gulf War). We revisit this result by using the robust Bayesian approach – implemented using our sampler – to quantify the informativeness of the different restrictions. Systematically assessing the role of these different identifying restrictions in shaping posterior inferences would be computationally costly when using accept-reject sampling to characterise the bounds of identified sets.
Figure 7 plots sets of posterior medians for the impulse responses obtained under three different sets of restrictions: 1) the ‘baseline’ model that imposes the sign and elasticity restrictions only; 2) the baseline model plus a single narrative restriction related to the August 1990 episode; and 3) the full set of restrictions. Overall, it is apparent that imposing only the August 1990 restriction is sufficient to obtain results that are very close to those obtained under the full set of restrictions. Much of the identifying power in the full set of narrative restrictions is therefore attributable to the restriction on the August 1990 episode. Whether either set of narrative restrictions are imposed has little effect on estimates of the responses of production and oil prices to a supply shock.
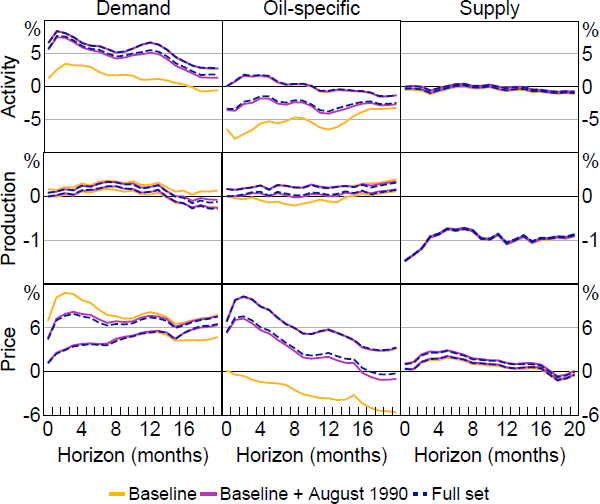
Note: ‘Baseline’ model imposes sign and elasticity restrictions; ‘Baseline + August 1990’ additionally imposes single narrative restriction based on August 1990 episode; ‘Full set’ imposes full set of narrative restrictions.
To quantify the informativeness of the restrictions, Appendix B.1.3 reports the ‘informativeness of restrictions’ statistic from Giacomini and Kitagawa (2021a). This is the amount by which the imposition of additional restrictions shrinks the set of posterior medians relative to some baseline model. Consistent with the discussion here, imposing only the August 1990 restriction yields informativeness statistics that are similar to those obtained under the full set of restrictions.
5.4 Empty identified sets
As noted above, the identified set may be empty. This section examines some issues related to emptiness of the identified set in the context of the empirical application. First, we show that our approach is better able to identify whether the identified set is non-empty and thus provides a better approximation of the ‘posterior plausibility’ of the identifying restrictions. Second, we consider augmenting the sampling algorithms with a step that screens out reduced-form parameter draws with empty identified sets before attempting to sample from .
5.4.1 Posterior plausibility
Giacomini and Kitagawa (2021a) suggest reporting the posterior probability that the identified set is non-empty – the posterior plausibility – as a measure of how consistent the identifying restrictions are with the observed data; see Giacomini, Kitagawa and Read (2022a) for further discussion of this concept or Amir-Ahmadi and Drautzburg (2021) for an application.
In the standard Bayesian exercise from Section 5.2, we approximate as being empty when none of the 1,000 candidate draws of Q from the accept-reject or slice samplers satisfy the identifying restrictions. Given that the number of candidate draws is finite, may be incorrectly classified as empty when it is actually non-empty. Based on the accept-reject sampler, the posterior plausibility is less than 1 per cent, which can be interpreted as indicating that the identifying restrictions are inconsistent with the joint distribution of the data. In contrast, the posterior plausibility is around 18 per cent when using our approach, so the identifying restrictions appear to be more compatible with the observed data than implied by the results from the accept-reject sampler. Our approach is substantially better able to determine whether is non-empty, despite using the same number of candidate draws of Q as the accept-reject sampler.
Increasing the number of draws of Q further improves the approximation of the posterior plausibility. For example, in the robust Bayesian exercise of Section 5.3, where we use around 25,000 draws of Q, the posterior plausibility is 25 per cent. For the accept-reject sampler to classify as non-empty with a similar degree of accuracy, it would be necessary to greatly increase the number of draws of Q required before approximating the identified set as empty, which would further increase its computational burden.
5.4.2 Empty identified sets and computational performance
The low posterior plausibilities reported above imply that part of the computational burden of sampling in the current application reflects repeated attempts to draw Q when may in fact be empty. If we could determine whether is empty before attempting to draw Q, we could potentially improve the computational efficiency of both samplers. While there exist algorithms to verify whether identified sets are (non-)empty (e.g. Amir-Ahmadi and Drautzburg 2021; Giacomini et al 2022; Read 2022), these are not directly applicable under the identifying restrictions that we consider here. We therefore explore checking a sufficient condition for emptiness (equivalently, a necessary condition for non-emptiness) of before attempting to draw values of Q. Intuitively, if the identified set is empty given a relaxed set of restrictions, the identified set must be empty when imposing the full set of restrictions, in which case we should redraw .
More specifically, consider imposing only the subset of restrictions that can be expressed as linear inequality restrictions on vec(Q). In the current application, these are the restrictions on impulse responses, elasticities and shock signs. Let the relaxed set of restrictions be represented as . Following ideas in Amir-Ahmadi and Drautzburg (2021), we check for the existence of a non-degenerate Chebychev centre within the ‘constrained set’, which is the intersection of the half spaces generated by the sign restrictions and the unit hypercube in . The Chebychev centre is the centre of the largest ball that can be inscribed within the constrained set, and is non-degenerate if and only if the radius of the ball is strictly positive. Clearly, if the Chebychev centre of this constrained set is degenerate, must be empty, since the restrictions represented in are weaker than the full set of restrictions. The Chebychev centre and the radius of the ball can be computed by solving a simple linear program.[26]
We re-run the exercise in Section 5.2 (with = 10–5), checking the sufficient condition for empty before attempting to draw values of Q satisfying the full set of restrictions. If the sufficient condition is satisfied, we redraw . Incorporating this step has little effect on the speed of the accept-reject sampler; the sampler still takes around 80 hours to generate the desired number of draws from the posterior. In contrast, including this step appears to increase the speed of our sampler; it now takes around 2 hours to generate the target number of draws compared with around 3.8 hours in the original exercise.
5.5 Additional application: US monetary policy shocks
In Appendix B.2, we explore the performance of our approach in a larger model. The model is from Antolín-Díaz and Rubio-Ramírez (2018), and is a six-variable SVAR of the US economy in which a monetary policy shock is identified using an extensive set of sign restrictions on impulse responses and narrative restrictions related to eight historical episodes. Obtaining 1,000 draws of Q at 1,000 draws of takes 20.1 hours using the accept-reject sampler, but only 1.4 hours using our approach. The average effective sample size from the slice sampler is 73.9 per cent, so our approach generates about 520,000 effective draws per hour, compared with about 50,000 effective draws per hour for the accept-reject sampler. We conclude that our approach continues to perform favourably in a larger model.
6. Conclusion
We develop a new approach to posterior sampling in sign-restricted SVARs under the commonly used uniform prior for the orthonormal matrix. This approach can also be used when conducting prior-robust Bayesian inference. The key feature of the approach is that it samples from a target density that smoothly penalises parameter values that violate (or are close to violating) the identifying restrictions, which allows us to apply MCMC methods. Our approach is broadly applicable under a wide range of identifying restrictions, including elasticity and narrative restrictions. We provide evidence that our approach is more computationally efficient than brute force accept-reject sampling when the identified set for the orthonormal matrix is assigned small measure under the uniform prior. It is therefore likely to be particularly useful when rich sets of identifying restrictions are imposed.
Future work could investigate whether our approach could be made more efficient by using alternative MCMC samplers that exploit local information about the shape of the smoothed target density (e.g. gradients). It is also likely that the use of alternative MCMC samplers would be necessary in large models, since the slice sampler can become inefficient in high dimensions. A promising area for future work may be to extend our approach to allow for zero restrictions (e.g. Arias et al 2018; Giacomini and Kitagawa 2021a; Read 2022), which would further broaden its applicability.
Appendix A: Proofs
Proof of Proposition 1. The assumption on T ensures that and exist. We can write
Denote the normalising constants for and by Cf and , respectively. Without loss of generality, assume s = 1 so there is a single sign restriction . The right-hand side of Equation (A1) can be written as
Under Assumption 1,
The first term in Equation (A2) therefore goes to zero as by the monotone convergence theorem. In the second term of Equation (A2),
which similarly goes to zero.
Appendix B: Additional Empirical Results
B.1 Oil market shocks
B.1.1 Approximating identified sets
According to the upper bound in Theorem 3 of Montiel Olea and Nesbit (2021), the number of draws M required from inside the identified set to guarantee a misclassification error less than occurs with probability at least is , , where d is the dimension of the parameter region being approximated (i.e. the number of impulse responses). Setting d = 3 × 3 × 21 = 189 and yields M = 20,713.
This many draws is also consistent with other combinations of and . Following the recommendation in Montiel Olea and Nesbit (2021), Figure B1 plots the ‘iso-draw curve’, which traces out combinations of that support the target value of M.
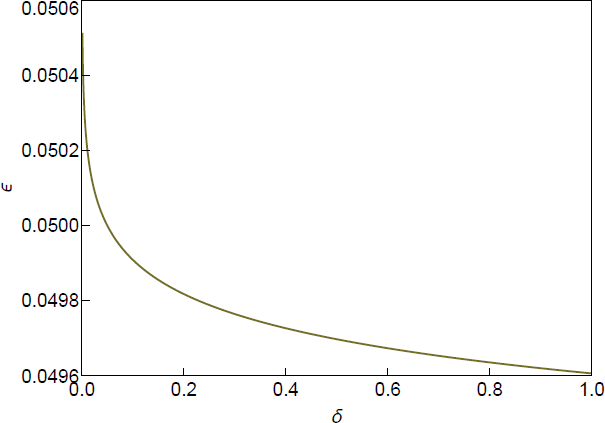
Note: Iso-draw curve plots pairs such that M = 20,713 draws from inside the identified set guarantees misclassification error less than with probability at least 1 – .
To obtain M effective draws from inside the identified set, we need to correct for the fact that the effective sample size is not 100 per cent (since some draws from the smoothed target density will violate the restrictions). We therefore gross up M using the average effective sample size from the exercise in Section 5.2. In that exercise, the average ESS was 82 per cent, so obtaining approximately M effective draws on average across the draws of requires approximately draws of Q from the smoothed target density.
B.1.2 Prior informativeness
Section 5.3.1 qualitatively discusses the role of the conditional prior for Q in driving posterior inferences about the effects of oil market shocks by comparing the results obtained under the standard and robust Bayesian approaches to inference. Giacomini and Kitagawa (2021a) suggest quantifying the influence of the conditional prior in driving posterior inferences using the ‘prior informativeness statistic’. This is the amount by which the selection of a single conditional prior narrows the credible intervals relative to the robust credible intervals:
When the parameter of interest is point identified, the credible and robust credible intervals coincide, the conditional prior has no influence on posterior inference, and the prior informativeness statistic is zero. Larger values indicate that the conditional prior contributes an increasing proportion of the information contained in the posterior.
We compute this statistic for the impulse response of each variable to each shock at each horizon, then average it over horizons (Table B1). Consistent with the discussion in Section 5.3.1, the prior informativeness statistic tends to be smaller for the responses to an oil supply shock than for the responses to other shocks. This indicates that the responses to an oil supply shock are more tightly identified, so the conditional prior contributes less of the apparent information in the posterior. The prior informativeness statistic averages less than 0.3 for all impulse responses, suggesting that the bulk of the information in the posterior is contributed by the data (given the identifying restrictions) rather than the conditional prior.
| Variable | Shock | ||
|---|---|---|---|
| Demand | Oil-specific | Supply | |
| Activity | 0.09 | 0.30 | 0.10 |
| Production | 0.20 | 0.23 | 0.06 |
| Price | 0.25 | 0.30 | 0.16 |
| Notes: Average of prior informativeness statistic over horizons. Higher values indicate that conditional prior has greater influence on posterior. | |||
B.1.3 Informativeness of identifying restrictions
Section 5.3.2 qualitatively assesses the identifying power of the narrative restrictions in the oil market model by comparing sets of posterior medians obtained under different identifying restrictions. The identifying power of restrictions can be quantified using a measure from Giacomini and Kitagawa (2021a). Let Ms be a model imposing a set of identifying restrictions and M1 be a model that relaxes the restrictions. For a given impulse response , the identifying power of the restrictions imposed in Ms beyond those imposed in M1 can be measured by:
This measures by how much the restrictions in Ms shrink the set of posterior medians compared with M1. If the additional restrictions in Ms are point identifying, the informativeness measure is one (because the set of posterior medians has zero width), while smaller values represent less additional identifying power in Ms relative to M1. Setting M1 as the ‘baseline’ model that imposes the sign and elasticity restrictions only, we compute the informativeness statistic for the two sets of narrative restrictions. For each variable and shock, Table B2 presents the average of the informativeness statistic over horizons.
| Variable | Shock | ||||||
|---|---|---|---|---|---|---|---|
| August 1990 | Full set of restrictions | ||||||
| Demand | Oil-specific | Supply | Demand | Oil-specific | Supply | ||
| Activity | 0.92 | 0.71 | 0.39 | 0.93 | 0.76 | 0.51 | |
| Production | 0.68 | 0.59 | 0.21 | 0.72 | 0.67 | 0.40 | |
| Price | 0.62 | 0.83 | 0.25 | 0.70 | 0.87 | 0.41 | |
| Notes: Average of informativeness of restrictions statistic over horizons. Informativeness is measured relative to ‘baseline’ model that imposes sign and elasticity restrictions only. Higher numbers indicate ‘more informative’ restrictions. | |||||||
The statistic obtained under the full set of restrictions is larger than when imposing the restriction based only on the August 1990 episode, since adding restrictions must (weakly) sharpen identification. But, consistent with the discussion in Section 5.3.2, the informativeness statistics under the two sets of narrative restrictions tend to be quite close. This implies that much of the identifying power in the full set of narrative restrictions is attributable to the restriction on the August 1990 episode.
B.2 Additional application: US monetary policy
To explore whether the favourable performance of our approach persists in a larger model, we use the monetary SVAR from Antolín-Díaz and Rubio-Ramírez (2018). They estimate the effects of monetary policy on the US economy using a six-variable SVAR in which the monetary policy shock is identified using an extensive set of sign restrictions on impulse responses and narrative restrictions.[27]
The reduced-form VAR is the same as in Uhlig (2005). The endogenous variables are real GDP (GDPt), the GDP deflator (GDPDEFt), a commodity price index (COMt), total reserves (TRt), non-borrowed reserves (NBRt) (all in natural logarithms) and the federal funds rate (FFRt); see Arias et al (2019) for details on the variables. The data are monthly and run from January 1965 to November 2007. The VAR includes a constant and 12 lags.
The sign restrictions on impulse responses to a monetary policy shock follow Uhlig (2005). The response of FFRt+h is non-negative for h = 0,1,...,5 and the responses of GDPDEFt+h, COMt+h and NBRt+h are non-positive for h = 0,1,...,5.
We impose the extended set of narrative restrictions from Antolín-Díaz and Rubio-Ramírez (2018). The restrictions are that the monetary policy shock was: positive in April 1974, October 1979, December 1988 and February 1994; negative in December 1990, October 1998, April 2001 and November 2002; and the most important contributor to the observed unexpected change in FFRt in these months. The implementation of the accept-reject sampler and our approach based on soft sign restrictions and the slice sampler is identical to that described in Section 5.2.
Obtaining the desired number of draws takes 20.1 hours using the accept-reject sampler, but only around 1.4 hours using our approach. The average effective sample size from the slice sampler is around 74 per cent, so our approach generates about 520,000 effective draws per hour, compared with about 50,000 effective draws per hour for the accept-reject sampler. Consistent with the results in Section 5.4, our approach also more accurately determines whether the identified set is non-empty; the posterior plausibility of the identifying restrictions based on our sampler is 43.6 per cent compared with only 5 per cent when using the accept-reject sampler.
Figure B2 summarises the posterior distributions of the impulse responses to a monetary policy shock obtained using the two samplers. The results are fairly similar, though the credible intervals based on the accept-reject sampler tend to be somewhat wider than those obtained using our sampler. This difference may reflect the ability of our sampler to better classify relatively small identified sets as non-empty. Overall, we conclude that our method continues to perform favourably in a larger SVAR.
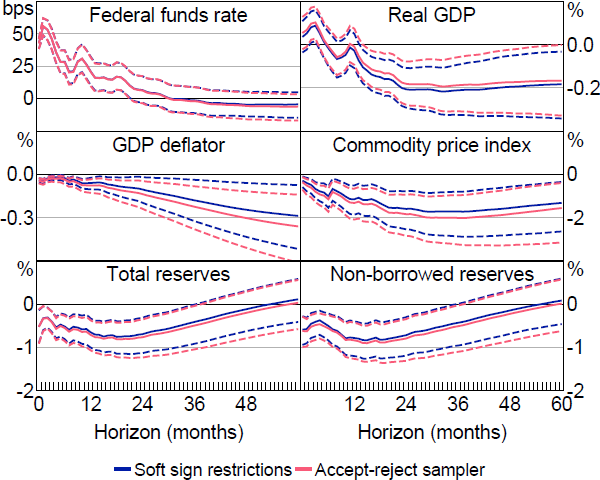
Note: Solid lines are posterior medians and dashed lines are 68 per cent credible intervals.
References
Amir-Ahmadi P and T Drautzburg (2021), ‘Identification and Inference with Ranking Restrictions’, Quantitative Economics, 12(1), pp 1–39.
Antolín-Díaz J and JF Rubio-Ramírez (2018), ‘Narrative Sign Restrictions for SVARs’, The American Economic Review, 108(10), pp 2802–2829.
Arias JE, D Caldara and JF Rubio-Ramírez (2019), ‘The Systematic Component of Monetary Policy in SVARs: An Agnostic Identification Procedure’, Journal of Monetary Economics, 101, pp 1–13.
Arias JE, JF Rubio-Ramírez and DF Waggoner (2018), ‘Inference Based on Structural Vector Autoregressions Identified with Sign and Zero Restrictions: Theory and Applications’, Econometrica, 86(2), pp 685–720.
Arias JE, JF Rubio-Ramírez and DF Waggoner (2021), ‘Inference in Bayesian Proxy-SVARs’, Journal of Econometrics, 225(1), pp 88–106.
Arias JE, JF Rubio-Ramírez and DF Waggoner (2025), ‘Uniform Priors for Impulse Responses’, Econometrica, 93(2), pp 695–718.
Bacchiocchi E, A Bastianin, T Kitagawa and E Mirto (2024), ‘Partially Identified Heteroskedastic SVARs’, Fondazione Eni Enrico Mattei Working Paper 15.2024.
Baumeister C and JD Hamilton (2015), ‘Sign Restrictions, Structural Vector Autoregressions, and Useful Prior Information’, Econometrica, 83(5), pp 1963–1999.
Baumeister C and JD Hamilton (2018), ‘Inference in Structural Vector Autoregressions when the Identifying Assumptions Are Not Fully Believed: Re-evaluating the Role of Monetary Policy in Economic Fluctuations’, Journal of Monetary Economics, 100, pp 48–65.
Baumeister C and JD Hamilton (2019), ‘Structural Interpretation of Vector Autoregressions with Incomplete Identification: Revisiting the Role of Oil Supply and Demand Shocks’, The American Economic Review, 109(5), pp 1873–1910.
Baumeister C and JD Hamilton (2024), ‘Advances in Using Vector Autoregressions to Estimate Structural Magnitudes’, Econometric Theory, 40(3), pp 472–510.
Baumeister C and G Peersman (2013), ‘The Role of Time-varying Price Elasticities in Accounting for Volatility Changes in the Crude Oil Market’, Journal of Applied Econometrics, 28(7), pp 1087–1109.
Braun R and R Brüggemann (2023), ‘Identification of SVAR Models by Combining Sign Restrictions with External Instruments’, Journal of Business & Economic Statistics, 41(4), pp 1077–1089.
Bruins M, JA Duffy, MP Keane and AA Smith, Jr (2018), ‘Generalized Indirect Inference for Discrete Choice Models’, Journal of Econometrics, 205(1), pp 177–203.
Bruns M and M Piffer (2023), ‘A New Posterior Sampler for Bayesian Structural Vector Autoregressive Models’, Quantitative Economics, 14(4), pp 1221–1250.
Carriero A, M Marcellino and T Tornese (2024), ‘Blended Identification in Structural VARs’, Journal of Monetary Economics, 146, Article 103581.
Chan JCC, M Matthes and X Yu (2025), ‘Large Structural VARs with Multiple Sign and Ranking Restrictions’, Unpublished manuscript, March. Available at <https://doi.org/10.48550/arXiv.2503.20668>.
Del Negro M and F Schorfheide (2011), ‘Bayesian Macroeconometrics’, in J Geweke, G Koop and H van Dijk (eds), The Oxford Handbook of Bayesian Econometrics, Oxford Handbooks, Oxford University Press, Oxford, pp 293–389.
Furlanetto F, A Lepetit, Robstad, J Rubio-Ramírez and P Ulvedal (2025), ‘Estimating Hysteresis Effects’, American Economic Journal: Macroeconomics, 17(1), pp 35–70.
Gafarov B, M Meier and JL Montiel Olea (2018), ‘Delta-method Inference for a Class of Set-identified SVARs’, Journal of Econometrics, 203(2), pp 316–327.
Giacomini R and T Kitagawa (2021a), ‘Robust Bayesian Inference for Set-identified Models’, Econometrica, 89(4), pp 1519–1556.
Giacomini R and T Kitagawa (2021b), ‘Supplement to “Robust Bayesian Inference for Set-identified Models”’, Econometrica, 89(4), Supporting Information, Online Appendix.
Giacomini R, T Kitagawa and M Read (2022a), ‘Narrative Restrictions and Proxies: Rejoinder’, Journal of Business & Economic Statistics, 40(4), pp 1438–1441.
Giacomini R, T Kitagawa and M Read (2022b), ‘Robust Bayesian Inference in Proxy SVARs’, Journal of Econometrics, 228(1), pp 107–126.
Giacomini R, T Kitagawa and M Read (2023), ‘Identification and Inference under Narrative Restrictions’, RBA Research Discussion Paper No 2023-07.
Giacomini R, T Kitagawa and M Read (forthcoming), ‘Robust Bayesian Analysis for Econometrics’, in V Chernozukhov, J Hörner, E La Ferrara and I Werning (eds), Advances in Economics and Econometrics: Twelfth World Congress: Volume 2, Econometric Society Monographs, Cambridge University Press, Cambridge.
Giacomini R, T Kitagawa and A Volpicella (2022), ‘Uncertain Identification’, Quantitative Economics, 13(1), pp 95–123.
Granziera E, HR Moon and F Schorfheide (2018), ‘Inference for VARs Identified With Sign Restrictions’, Quantitative Economics, 9(3), pp 1087–1121.
Hoesch L, A Lee and G Mesters (2024), ‘Locally Robust Inference for Non-Gaussian SVAR Models’, Quantitative Economics, 15(2), pp 523–570.
Hou C (2024), ‘Large Bayesian SVARs With Linear Restrictions’, Journal of Econometrics, 244(1), Article 105850.
Inoue A and L Kilian (2024), ‘When Is the Use of Gaussian-inverse Wishart-Haar Priors Appropriate?’, Federal Reserve Bank of Dallas Working Paper 2404.
Inoue A and L Kilian (2025), ‘The Conventional Impulse Response Prior in VAR Models with Sign Restrictions’, Centre for Economic Policy Research Discussion Paper DP20159.
Kilian L (2009), ‘Not All Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market’, The American Economic Review, 99(3), pp 1053–1069.
Kilian L and H Lütkepohl (2017), Structural Vector Autoregressive Analysis, Themes in Modern Econometrics, Cambridge University Press, Cambridge.
Kilian L and DP Murphy (2012), ‘Why Agnostic Sign Restrictions Are Not Enough: Understanding the Dynamics of Oil Market VAR Models’, Journal of the European Economic Association, 10(5), pp 1166–1188.
Kilian L and DP Murphy (2014), ‘The Role of Inventories and Speculative Trading in the Global Market for Crude Oil’, Journal of Applied Econometrics, 29(3), pp 454–478.
Lagarias JC, JA Reeds, MH Wright and PE Wright (1998), ‘Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions’, SIAM Journal on Optimization, 9(1), pp 112–147.
Liu G and LJ Hong (2011), ‘Kernel Estimation of the Greeks for Options with Discontinuous Payoffs’, Operations Research, 59(1), pp 96–108.
Ludvigson SC, S Ma and S Ng (2017), ‘Shock Restricted Structural Vector-autoregressions’, NBER Working Paper No 23225, rev January 2020.
Ludvigson SC, S Ma and S Ng (2021), ‘Uncertainty and Business Cycles: Exogenous Impulse or Endogenous Response?’, American Economic Journal: Macroeconomics, 13(4), pp 369–410.
Lütkepohl H and A Netšunajev (2014), ‘Disentangling Demand and Supply Shocks in the Crude Oil Market: How to Check Sign Restrictions in Structural VARs’, Journal of Applied Econometrics, 29(3), pp 479–496.
Mira A and L Tierney (2002), ‘Efficiency and Convergence Properties of Slice Samplers’, Scandinavian Journal of Statistics, 29(1), pp 1–12.
Montiel Olea JL and J Nesbit (2021), ‘(Machine) Learning Parameter Regions’, Journal of Econometrics, 221(1, Part C), pp 716–744.
Moon HR and F Schorfheide (2012), ‘Bayesian and Frequentist Inference in Partially Identified Models’, Econometrica, 80(2), pp 755–782.
Neal RM (2003), ‘Slice Sampling’, Annals of Statistics, 31(3), pp 705–767.
Poirier DJ (1998), ‘Revising Beliefs in Nonidentified Models’, Econometric Theory, 14(4), pp 483–509.
Read M (2022), ‘Algorithms for Inference in SVARs Identified with Sign and Zero Restrictions’, The Econometrics Journal, 25(3), pp 699–718.
Read M (forthcoming), ‘Set-identified Structural Vector Autoregressions and the Effects of a 100 Basis Point Monetary Policy Shock’, The Review of Economics and Statistics.
Roberts GO and JS Rosenthal (1999), ‘Convergence of Slice Sampler Markov Chains’, Journal of the Royal Statistical Society Series B: Statistical Methodology, 61(3), pp 643–660.
Rothenberg TJ (1971), ‘Identification in Parametric Models’, Econometrica, 39(3), pp 577–591.
Rubio-Ramírez JF, DF Waggoner and T Zha (2010), ‘Structural Vector Autoregressions: Theory of Identification and Algorithms for Inference’, The Review of Economic Studies, 77(2), pp 665–696.
Souris A, A Bhattacharya and D Pati (2019), ‘The Soft Multivariate Truncated Normal Distribution with Applications to Bayesian Constrained Estimation’, Unpublished manuscript, Texas A&M University, 2 September. Available at <https://doi.org/10.48550/arXiv.1807.09155>.
Stewart GW (1980), ‘The Efficient Generation of Random Orthogonal Matrices with an Application to Condition Estimators’, SIAM Journal on Numerical Analysis, 17(3), pp 403–409.
Stock JH and MW Watson (2016), ‘Dynamic Factor Models, Factor-augmented Vector Autoregressions, and Structural Vector Autoregressions in Macroeconomics’, in JB Taylor and H Uhlig (eds), Handbook of Macroeconomics: Volume 2A, Handbooks in Economics, Elsevier, Amsterdam, pp 415–525.
Uhlig H (2005), ‘What Are the Effects of Monetary Policy on Output? Results From an Agnostic Identification Procedure’, Journal of Monetary Economics, 52(2), pp 381–419.
Uhlig H (2017), ‘Shocks, Sign Restrictions, and Identification’, in B Honoré, A Pakes, M Piazzesi and L Samuelson (eds), Advances in Economics and Econometrics: Eleventh World Congress: Volume 2, Econometric Society Monographs, Cambridge University Press, Cambridge, pp 95–127.
Volpicella A (2022), ‘SVARs Identification through Bounds on the Forecast Error Variance’, Journal of Business & Economic Statistics, 40(3), pp 1291–1301.
Acknowledgements
We thank Joshua Chan, Thorsten Drautzburg, Toru Kitagawa, James Morley, Yong Song and Benjamin Wong for helpful comments. We also thank participants at the 2023 Continuing Education in Macroeconometrics workshop, the 2023 Time Series and Forecasting Symposium and the 2024 Econometric Society Australasia Meeting. The views expressed in this paper are those of the authors and should not be attributed to the Reserve Bank of Australia. Any errors are the sole responsibility of the authors.
Footnotes
See the references in Baumeister and Hamilton (2018) for many such examples. There is ongoing debate about the appropriateness of this prior (e.g. Inoue and Kilian 2024; Arias, Rubio-Ramírez and Waggoner 2025). For frequentist approaches to inference in this setting, see Gafarov, Meier and Montiel Olea (2018) or Granziera, Moon and Schorfheide (2018). [1]
The identified set is the set of observationally equivalent parameter values, which are parameter values sharing the same value of the likelihood. [2]
Hou (2024) proposes an MCMC algorithm for posterior sampling under (potentially overidentifying) linear equality and inequality restrictions on impact impulse responses. The algorithm can incorporate inequality restrictions on other parameters, though this requires additional accept-reject steps. The posterior corresponds to an independent Gaussian prior over the columns of the impact impulse-response matrix, rather than the uniform prior for Q considered here. [3]
Variants of this model have been widely studied elsewhere (e.g. Baumeister and Peersman 2013; Lütkepohl and Netšunajev 2014; Baumeister and Hamilton 2019; Bacchiocchi et al 2024; Carriero, Marcellino and Tornese 2024; Hoesch, Lee and Mesters 2024). [4]
See Stock and Watson (2016) or Kilian and Lütkepohl (2017) for overviews of identification in SVARs. [5]
Restrictions on the contribution of shock j to the realisation of (as opposed to the forecast error in) variable i could be imposed by placing restrictions on Hi,j,1,t. [6]
To be clear, our approach cannot handle exogeneity restrictions related to proxy variables, since these are equivalent to zero restrictions. [7]
Some types of restrictions depend on other parameters or objects not captured in the current definition of . For instance, narrative restrictions depend on the data in specific periods via the reduced-form VAR innovations (Antolín-Díaz and Rubio-Ramírez 2018; Giacomini et al 2023). We leave this potential dependence implicit. [8]
An alternative approach is to obtain the bounds by solving a numerical optimisation problem using, for example, gradient-based methods, but this can be computationally burdensome and convergence to the true bounds is not always guaranteed (e.g. Amir-Ahmadi and Drautzburg 2021; Giacomini and Kitagawa 2021a; Montiel Olea and Nesbit 2021). Gafarov et al (2018) propose an active-set algorithm for computing the bounds, but this is only applicable when there are linear restrictions on a single column of Q; their algorithm can also become burdensome when there are many restrictions (Read 2022). [9]
As discussed in Neal (2003), extensions of the slice sampler can make use of local information about the shape of the target density, such as by using local quadratic approximations based on the derivatives of the log target density. The regularised constraints that we use allow us in principle to construct such approximations. Further work could potentially improve the efficiency of our approach by using this information. [12]
In this example, the sign normalisations on the diagonal elements of A0 are redundant given the sign restrictions. [15]
In this exercise, the slice sampler is initialised at a random draw of Z from a matrix standard normal distribution. [16]
The results are obtained using Matlab R2023a on a desktop computer running Microsoft Windows 10 Enterprise with an Intel Core i7-9700 CPU @ 3.00GHz, 8 cores and 128 GB RAM. [17]
This expression implicitly assumes otherwise the first interval is empty. [18]
The data were obtained from the replication files to Antolín-Díaz and Rubio-Ramírez (2018). [19]
Baumeister and Hamilton (2024) argue that ratios of impulse responses cannot be interpreted as structural elasticities except in bivariate models; instead, structural elasticities are given by ratios of elements of A0. We impose the same elasticity restrictions as in Antolín-Díaz and Rubio-Ramírez (2018), who in turn follow Kilian and Murphy (2012), to maintain comparability. [20]
Antolín-Díaz and Rubio-Ramírez (2018) state that the oil supply shock is negative in these periods, which reflects a convention of referring to supply shocks that lower production as negative. However, given the sign restrictions in Equation (18), a positive supply shock results in lower oil production and an increase in the price of oil. Hence, although the language that we use to describe the sign of the shock differs, the economic content of the restriction is the same. [21]
The results are also consistent with those presented in Antolín-Díaz and Rubio-Ramírez (2018), despite some differences in the details of the exercise. The results are not directly comparable for two main reasons. First, as discussed above, we use a conditionally uniform prior for Q. Second, following the recommendation in Giacomini et al (2023), we construct the posterior distribution using the unconditional likelihood rather than the conditional likelihood; this means that the importance-sampling step in Antolín-Díaz and Rubio-Ramírez (2018) – which reweights posterior draws based on the ex ante probability that the shocks satisfy the narrative restrictions – is unnecessary. [24]
To more systematically quantify the influence of the conditional prior, Appendix B.1.2 reports the ‘prior informativeness’ statistic from Giacomini and Kitagawa (2021a). This is the amount by which the selection of the single (uniform) conditional prior narrows the standard credible intervals relative to the robust credible intervals. Consistent with the informal discussion here, the prior informativeness statistic is smaller for the responses of oil supply shocks than for the other responses. [25]
See Giacomini et al (2023) for a robust Bayesian treatment of this application. [27]