RDP 2025-03: Fast Posterior Sampling in Tightly Identified SVARs Using ‘Soft’ Sign Restrictions 5. Empirical Application: Demand and Supply Shocks in the Oil Market
May 2025
- Download the Paper 1.45MB
To explore the performance of the algorithms in an empirical setting, we consider the model of the global oil market in Antolín-Díaz and Rubio-Ramírez (2018), which builds on Kilian (2009) and Kilian and Murphy (2012). We select this application because it involves a rich set of identifying restrictions – sign restrictions, elasticity restrictions and narrative restrictions – that (nonlinearly) constrains all columns of Q. It is therefore a useful setting in which to illustrate the broad applicability of our sampling approach. We compare the performance of our approach against accept-reject sampling when conducting standard Bayesian inference under the usual uniform prior. We also demonstrate the utility of our approach when conducting prior-robust Bayesian inference, including by using robust Bayesian methods to quantify the importance of different narrative restrictions in driving inferences about the effects of oil market shocks.
5.1 Model and identifying restrictions
The model's endogenous variables are an index of real economic activity (REAt), the growth rate of global oil production (PRODt) and the log of the real price of oil (RPOt). The VAR includes 24 lags and a constant, and is estimated on monthly data from January 1971 to December 2015.[19] The reduced-form prior is a diffuse normal-inverse-Wishart distribution, so the posterior is also normal-inverse-Wishart (e.g. Del Negro and Schorfheide 2011).
Let yt = (REAt, PRODt, RPOt)′. The following sign restrictions are imposed on the impact impulse responses:
These restrictions imply that the model's three structural shocks can be interpreted as shocks to aggregate demand, oil-specific demand and oil supply, respectively. Each of these sign restrictions can be written as a linear inequality restriction on a single column of Q.
The ‘price elasticity of oil supply’ is restricted to be less than 0.0258, which Kilian and Murphy (2012) argue is a credible upper bound based on existing evidence. This elasticity is defined as the ratio of the impact response of production growth to the impact response of the real price of oil following aggregate demand or oil-specific demand shocks, so the restrictions are:[20]
The narrative restrictions include restrictions on the signs of the structural shocks in specific periods (‘shock-sign restrictions’), as well as their contributions to one-step-ahead forecast errors (i.e. historical decompositions). The shock-sign restrictions are that the oil supply shock was non-negative in December 1978, January 1979, September 1980, October 1980, August 1990, December 2002, March 2003 and February 2011, which are months in which narrative accounts suggest that there were unexpected disruptions in oil production.[21] These restrictions require that
for values of t corresponding to the dates listed above. Each of these restrictions is a linear inequality restriction on a single column of Q. The restrictions on the historical decomposition include the restriction that the oil supply shock was the ‘most important contributor’ to the observed unexpected movement in oil production growth in these months. This requires that . Finally, for the periods September 1980, October 1980 and August 1990, aggregate demand shocks are restricted to be the ‘least important contributor’ to the unexpected movement in the real price of oil, which requires that . These are nonlinear restrictions that simultaneously constrain all columns of Q.[22]
5.2 Standard Bayesian inference
The goal of our first exercise is to obtain 1,000 draws of from its posterior (such that the identified set is non-empty) and 1,000 draws of Q from the uniform distribution over at each draw of , yielding 106 draws of the impulse responses given the conditionally uniform normal-inverse-Wishart prior. We do this using the accept-reject sampler and our approach based on soft sign restrictions and the slice sampler.
As noted in Section 2.3, the identified set may be empty. When using the accept-reject sampler, we make 1,000 unsuccessful attempts to draw Q before approximating as empty and redrawing . When using the slice sampler, if none of the 1,000 draws of Q satisfy the identifying restrictions, we redraw . Similar computational effort is therefore used to determine whether the identified set is non-empty under both approaches.
At each draw of , we find an initial value for the slice sampler by using a numerical optimisation routine to find a (potentially local) maximum of the log target density with = 0.1; experiments suggest that this initialisation strategy increases the efficiency of the sampler relative to initialising at a random draw.[23] We set = 10–5 when sampling and examine alternative choices below.
Figure 5 summarises the posterior distributions of the impulse responses obtained using the two samplers. The results are very similar.[24] The accept-reject sampler takes around 80 hours to generate the desired number of draws from the posterior, whereas the slice sampler takes only 3.8 hours. The effective sample size (as a percentage of the original sample size) from the slice sampler is around 82 per cent. To adjust for the difference in effective sample size, we compare the number of effective draws per hour, which is the effective sample size divided by the number of hours taken to obtain the draws. The accept-reject sampler generates approximately 12,400 draws per hour, whereas the slice sampler generates around 210,000 effective draws per hour. On this basis, our approach is an order of magnitude more computationally efficient than accept-reject sampling, generating around 17 times as many effective draws per unit of time.
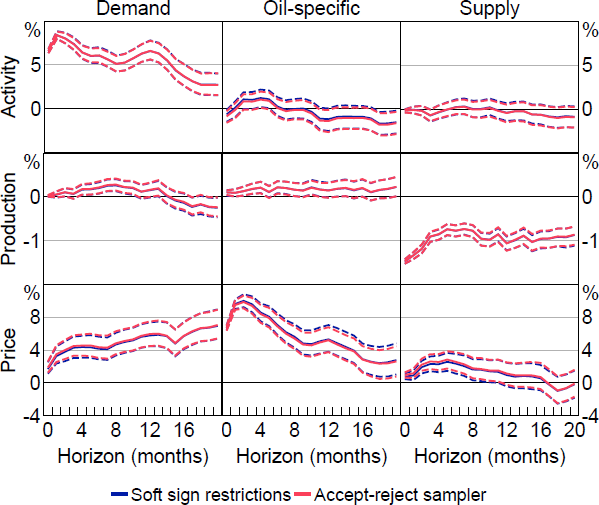
Note: Solid lines are posterior medians and dashed lines are 68 per cent credible intervals.
Figure 5 suggests that the posterior distributions of the impulse responses generated by the samplers are similar. However, as discussed in Section 3.2, our approach samples from an approximation of the uniform distribution over , where the approximation error vanishes as . We can examine the magnitude of the approximation error by comparing the distributions of the draws obtained using the two samplers at a fixed value of . Using a random draw of from its posterior, quantile-quantile plots and two-sample Kolmogorov-Smirnov test statistics suggest that, while some differences in distributions are apparent across the two samplers, the differences tend to be quantitatively small. These quantitatively small differences appear to largely wash out when averaging over (noting that our algorithm is better able to determine whether the identified set is non-empty, which will also generates differences in the approximated posterior distributions, as discussed in Section 5.4 below).
The results in this section have been obtained with the penalisation parameter set to 10–5. However, does not have a natural scale, so the choice of this parameter is somewhat arbitrary. Table 2 compares the computational performance of our sampler at different choices of . For all values of considered, our sampler generates more effective draws per hour than the accept-reject sampler. Effective draws per hour are maximised at = 10–3 and decline slowly as increases. Choosing small values of to mitigate bias is therefore feasible without large sacrifices in terms of computational efficiency.
| Algorithm | Speed (hours) | Effective draws per hour (′000) |
|---|---|---|
| Accept-reject | 77.0 | 13 |
| Soft sign restrictions: | ||
| = 10–1 | 1.4 | 36 |
| = 10–2 | 2.1 | 167 |
| = 10–3 | 2.8 | 254 |
| = 10–4 | 3.4 | 234 |
| = 10–5 | 3.8 | 209 |
| = 10–6 | 4.4 | 184 |
|
Notes: controls penalisation of parameter values that violate (or are close to violating) sign restrictions in slice sampler. Effective draws per hour rounded to nearest thousand. |
||
5.3 Robust Bayesian inference
Our second empirical exercise exploits our sampling approach to implement the prior-robust Bayesian inferential procedure proposed in Giacomini and Kitagawa (2021a). Following an algorithm proposed in Giacomini and Kitagawa, we approximate the bounds of the identified set for each impulse response by computing the minimum and maximum of over a large number of draws from . These approximations will possess error that will vanish as the number of draws of Q goes to infinity. An important consideration when using this approach is therefore the number of draws of Q used to approximate the bounds.
Montiel Olea and Nesbit (2021) derive results about the number of draws required to approximate identified sets up to a desired degree of accuracy. Based on their results, if we want to guarantee a misclassification error less than 5 per cent with probability at least 95 per cent, we require over 20,000 draws from at each draw of . From the exercise in Section 5.2, it is clear that implementing the robust Bayesian approach to inference with this target level of accuracy would be extremely computationally costly. We therefore turn to our algorithms based on soft sign restrictions. See Appendix B.1.1 for details about how we implement our approach in this exercise.
5.3.1 Assessing prior sensitivity
Figure 6 plots the set of posterior medians and 68 per cent robust credible intervals for the impulse responses, which are summaries of the class of posteriors obtained under the prior-robust Bayesian procedure (see Section 2.4). These quantities can be used to assess the influence of the conditional prior on the posterior; intuitively, if the set of posterior medians is ‘wide’ and/or the robust credible intervals are substantially wider than the standard credible intervals, the conditional prior contributes a lot of the apparent information in the posterior, and posterior inferences may be sensitive to the choice of conditional prior. For comparison, Figure 6 also plots the posterior median and 68 per cent credible interval obtained under the standard Bayesian approach to inference with a conditionally uniform prior for Q.
The influence of the conditional prior on the posterior varies somewhat across different impulse responses. For the oil supply shock, the set of posterior medians tends to be narrow, and the robust credible intervals are similar in width to the standard credible intervals. In other words, the responses to an oil supply shock are tightly identified and the conditional prior has little influence on posterior inferences about these responses. For demand-side shocks, the influence of the conditional prior is more noticeable in some cases, particularly for the response of oil prices and the response of activity to an oil-specific demand shock. This indicates that these responses are less tightly identified and the conditional prior contributes more of the apparent information in the posterior.[25] Nevertheless, even in these cases, the robust credible intervals tend to exclude zero in the same cases where the standard credible intervals exclude zero. Overall, this suggests that inferences about the effects of shocks in the oil market obtained under this rich set of identifying restrictions are not particularly sensitive to the choice of conditional prior for Q.
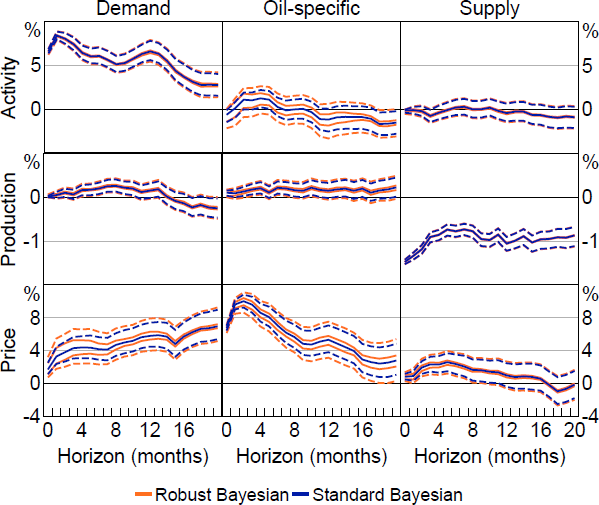
Notes: Solid lines are (sets of) posterior medians and dashed lines are 68 per cent (robust) credible intervals. Results obtained using soft sign restrictions.
Importantly, the large number of draws of Q used to approximate the identified set and the guarantee on approximation accuracy from Montiel Olea and Nesbit (2021) mean that this apparent robustness to the choice of conditional prior is unlikely to be an artefact of approximation error. These results complement exercises in Inoue and Kilian (2024), who highlight applications where posterior inferences do not appear to be driven by the uniform prior for Q.
5.3.2 Assessing the importance of the narrative restrictions
Antolín-Díaz and Rubio-Ramírez (2018) show that their results can largely be replicated by replacing the set of narrative restrictions with a single narrative restriction. In particular, alongside the sign and elasticity restrictions, they consider imposing the narrative restriction that aggregate demand shocks were the least important contributor to the unexpected movement in the real price of oil in August 1990 (corresponding to the start of the Gulf War). We revisit this result by using the robust Bayesian approach – implemented using our sampler – to quantify the informativeness of the different restrictions. Systematically assessing the role of these different identifying restrictions in shaping posterior inferences would be computationally costly when using accept-reject sampling to characterise the bounds of identified sets.
Figure 7 plots sets of posterior medians for the impulse responses obtained under three different sets of restrictions: 1) the ‘baseline’ model that imposes the sign and elasticity restrictions only; 2) the baseline model plus a single narrative restriction related to the August 1990 episode; and 3) the full set of restrictions. Overall, it is apparent that imposing only the August 1990 restriction is sufficient to obtain results that are very close to those obtained under the full set of restrictions. Much of the identifying power in the full set of narrative restrictions is therefore attributable to the restriction on the August 1990 episode. Whether either set of narrative restrictions are imposed has little effect on estimates of the responses of production and oil prices to a supply shock.
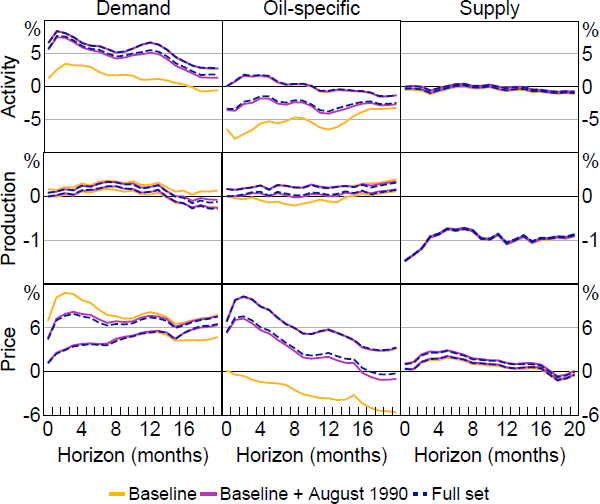
Note: ‘Baseline’ model imposes sign and elasticity restrictions; ‘Baseline + August 1990’ additionally imposes single narrative restriction based on August 1990 episode; ‘Full set’ imposes full set of narrative restrictions.
To quantify the informativeness of the restrictions, Appendix B.1.3 reports the ‘informativeness of restrictions’ statistic from Giacomini and Kitagawa (2021a). This is the amount by which the imposition of additional restrictions shrinks the set of posterior medians relative to some baseline model. Consistent with the discussion here, imposing only the August 1990 restriction yields informativeness statistics that are similar to those obtained under the full set of restrictions.
5.4 Empty identified sets
As noted above, the identified set may be empty. This section examines some issues related to emptiness of the identified set in the context of the empirical application. First, we show that our approach is better able to identify whether the identified set is non-empty and thus provides a better approximation of the ‘posterior plausibility’ of the identifying restrictions. Second, we consider augmenting the sampling algorithms with a step that screens out reduced-form parameter draws with empty identified sets before attempting to sample from .
5.4.1 Posterior plausibility
Giacomini and Kitagawa (2021a) suggest reporting the posterior probability that the identified set is non-empty – the posterior plausibility – as a measure of how consistent the identifying restrictions are with the observed data; see Giacomini, Kitagawa and Read (2022a) for further discussion of this concept or Amir-Ahmadi and Drautzburg (2021) for an application.
In the standard Bayesian exercise from Section 5.2, we approximate as being empty when none of the 1,000 candidate draws of Q from the accept-reject or slice samplers satisfy the identifying restrictions. Given that the number of candidate draws is finite, may be incorrectly classified as empty when it is actually non-empty. Based on the accept-reject sampler, the posterior plausibility is less than 1 per cent, which can be interpreted as indicating that the identifying restrictions are inconsistent with the joint distribution of the data. In contrast, the posterior plausibility is around 18 per cent when using our approach, so the identifying restrictions appear to be more compatible with the observed data than implied by the results from the accept-reject sampler. Our approach is substantially better able to determine whether is non-empty, despite using the same number of candidate draws of Q as the accept-reject sampler.
Increasing the number of draws of Q further improves the approximation of the posterior plausibility. For example, in the robust Bayesian exercise of Section 5.3, where we use around 25,000 draws of Q, the posterior plausibility is 25 per cent. For the accept-reject sampler to classify as non-empty with a similar degree of accuracy, it would be necessary to greatly increase the number of draws of Q required before approximating the identified set as empty, which would further increase its computational burden.
5.4.2 Empty identified sets and computational performance
The low posterior plausibilities reported above imply that part of the computational burden of sampling in the current application reflects repeated attempts to draw Q when may in fact be empty. If we could determine whether is empty before attempting to draw Q, we could potentially improve the computational efficiency of both samplers. While there exist algorithms to verify whether identified sets are (non-)empty (e.g. Amir-Ahmadi and Drautzburg 2021; Giacomini et al 2022; Read 2022), these are not directly applicable under the identifying restrictions that we consider here. We therefore explore checking a sufficient condition for emptiness (equivalently, a necessary condition for non-emptiness) of before attempting to draw values of Q. Intuitively, if the identified set is empty given a relaxed set of restrictions, the identified set must be empty when imposing the full set of restrictions, in which case we should redraw .
More specifically, consider imposing only the subset of restrictions that can be expressed as linear inequality restrictions on vec(Q). In the current application, these are the restrictions on impulse responses, elasticities and shock signs. Let the relaxed set of restrictions be represented as . Following ideas in Amir-Ahmadi and Drautzburg (2021), we check for the existence of a non-degenerate Chebychev centre within the ‘constrained set’, which is the intersection of the half spaces generated by the sign restrictions and the unit hypercube in . The Chebychev centre is the centre of the largest ball that can be inscribed within the constrained set, and is non-degenerate if and only if the radius of the ball is strictly positive. Clearly, if the Chebychev centre of this constrained set is degenerate, must be empty, since the restrictions represented in are weaker than the full set of restrictions. The Chebychev centre and the radius of the ball can be computed by solving a simple linear program.[26]
We re-run the exercise in Section 5.2 (with = 10–5), checking the sufficient condition for empty before attempting to draw values of Q satisfying the full set of restrictions. If the sufficient condition is satisfied, we redraw . Incorporating this step has little effect on the speed of the accept-reject sampler; the sampler still takes around 80 hours to generate the desired number of draws from the posterior. In contrast, including this step appears to increase the speed of our sampler; it now takes around 2 hours to generate the target number of draws compared with around 3.8 hours in the original exercise.
5.5 Additional application: US monetary policy shocks
In Appendix B.2, we explore the performance of our approach in a larger model. The model is from Antolín-Díaz and Rubio-Ramírez (2018), and is a six-variable SVAR of the US economy in which a monetary policy shock is identified using an extensive set of sign restrictions on impulse responses and narrative restrictions related to eight historical episodes. Obtaining 1,000 draws of Q at 1,000 draws of takes 20.1 hours using the accept-reject sampler, but only 1.4 hours using our approach. The average effective sample size from the slice sampler is 73.9 per cent, so our approach generates about 520,000 effective draws per hour, compared with about 50,000 effective draws per hour for the accept-reject sampler. We conclude that our approach continues to perform favourably in a larger model.
Footnotes
The data were obtained from the replication files to Antolín-Díaz and Rubio-Ramírez (2018). [19]
Baumeister and Hamilton (2024) argue that ratios of impulse responses cannot be interpreted as structural elasticities except in bivariate models; instead, structural elasticities are given by ratios of elements of A0. We impose the same elasticity restrictions as in Antolín-Díaz and Rubio-Ramírez (2018), who in turn follow Kilian and Murphy (2012), to maintain comparability. [20]
Antolín-Díaz and Rubio-Ramírez (2018) state that the oil supply shock is negative in these periods, which reflects a convention of referring to supply shocks that lower production as negative. However, given the sign restrictions in Equation (18), a positive supply shock results in lower oil production and an increase in the price of oil. Hence, although the language that we use to describe the sign of the shock differs, the economic content of the restriction is the same. [21]
The results are also consistent with those presented in Antolín-Díaz and Rubio-Ramírez (2018), despite some differences in the details of the exercise. The results are not directly comparable for two main reasons. First, as discussed above, we use a conditionally uniform prior for Q. Second, following the recommendation in Giacomini et al (2023), we construct the posterior distribution using the unconditional likelihood rather than the conditional likelihood; this means that the importance-sampling step in Antolín-Díaz and Rubio-Ramírez (2018) – which reweights posterior draws based on the ex ante probability that the shocks satisfy the narrative restrictions – is unnecessary. [24]
To more systematically quantify the influence of the conditional prior, Appendix B.1.2 reports the ‘prior informativeness’ statistic from Giacomini and Kitagawa (2021a). This is the amount by which the selection of the single (uniform) conditional prior narrows the standard credible intervals relative to the robust credible intervals. Consistent with the informal discussion here, the prior informativeness statistic is smaller for the responses of oil supply shocks than for the other responses. [25]