RDP 2021-09: Is the Phillips Curve Still a Curve? Evidence from the Regions 7. Comparison to Aggregate Models

7.1 The RBA wage Phillips curve

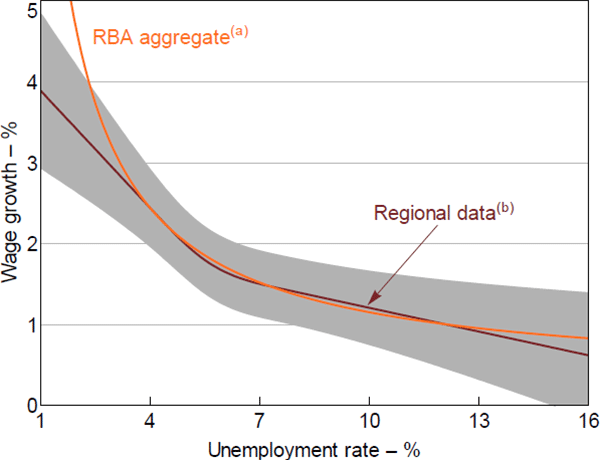
One of the motivations for this paper was to test whether the functional form that underlies the RBA's Phillips curves is sensible. To examine this, Figure 9 compares our estimates of the slope and curvature of the Phillips curve using the cubic spline (regional data) to the RBA's estimates using the Debelle and Vickery (1997) functional form (aggregate data). The ‘RBA aggregate’ line in Figure 9 plots the curve implied by plugging the annualised estimated model coefficient, $\gamma$, from the RBA's current aggregate wage Phillips curve equation set out in Appendix A into Equation (2) for each level of unemployment.^[38] The ‘Regional data’ line plots the curve implied by the results from our preferred cubic spline specification. In this figure, the vertical positions of both curves are arbitrarily pinned down based on an assumption that wages growth will equal 2.2 per cent when the unemployment rate is 4.5 per cent.

For unemployment rates above 3½ per cent, the slopes of the two curves are virtually identical. The fact that the estimates are so close is perhaps surprising, given that they are based on data at different levels of aggregation and use different sources of variation. It is only when the unemployment rate falls below 3½ per cent that a gap between the two sets of estimates opens up - in the RBA's aggregate model, wages growth starts to increase rapidly, whereas in our model the response of wages growth is more muted.

Overall, our results provide support for the RBA's existing modelling framework at the current juncture. The nonlinearity assumptions imposed by the RBA's wage Phillips curve model, together with the aggregate data, do a relatively good job of capturing the relationship at national unemployment rates above 3½ per cent. However, this assessment would need to be re-evaluated if the labour market were to tighten materially and the unemployment rate were to fall below 3½ per cent. If this were to happen, then our results would suggest caution in generating inflation forecasts using the highly nonlinear response of wages growth and inflation currently embodied in the Debelle and Vickery (1997) specification. While wages growth and inflation would increase, our results suggest they would not rise exponentially.^[39]

Implicit in this comparison between the RBA's aggregate model and our regional model is the assumption that estimates from the latter can be reliably compared to the former. We turn to this below.

7.2 Aggregation issues

Does it make sense to infer the slope of the aggregate Phillips curve based on regional variation in wages and prices?

This question has been posed by other papers in this field. To clarify thinking around this issue, a number of these papers develop theoretical frameworks that link the parameters estimated using regional variation (in a panel model with time fixed effects) to the structural parameter that policymakers ultimately care about – the slope of the national Phillips curve. These papers take a typical single economy New Keynesian model and adapt it to the case where there are many distinct regions. In these models, each region is part of a monetary union – for example, individual states within the United States, or individual countries within the euro area. Hazell et al (2020) and Fitzgerald et al (2020) develop this type of model for the price Phillips curve, while Levy (2019) does the same for the wage Phillips curve.

These models clarify that estimates of the Phillips curve based on regional variation are informative about the slope of the ‘structural’ Phillips curve facing policymakers. Indeed, as discussed in Section 3.1, these models highlight how regional variation helps to overcome the endogeneity issues that can face an econometrician when using national time series data. However, the models also show that there are some factors we need to keep in mind when translating regional estimates into aggregate ones.

7.2.1 Nationally-set wages

One key insight from Hazell et al's (2020) model is that it is important to distinguish between tradeable and non-tradeable inflation when estimating the price Phillips curve using regional variation. By definition, non-tradeable goods and services are only consumed in the region in which they are produced, while the market for tradeable goods and services is fully integrated across regions. This means that consumers in different regions can face different prices for non-tradeables, but the same prices for tradeables. An implication is that the slope of the regional Phillips curve for overall inflation (aggregating both tradeables and non-tradeables) will understate its aggregate counterpart because the prices of tradeable goods at the regional level are insensitive to slack at the regional level. In other words, the regional CPI is less sensitive to regional unemployment than the aggregate CPI is to aggregate unemployment, because tradeable inflation is only affected by aggregate unemployment. For this reason, Hazell et al (2020) focus on non-tradeable inflation as the dependent variable in their analysis of regional data, and then use their estimates to make inferences about the slope of the Phillips curve for overall CPI at the national level.

The implications of Hazell et al's analysis are less clear when examining regional variation in wages. If labour is mobile across the tradeable and non-tradeable sectors within a region, then in theory wages should equalise within that region even if prices do not (Moretti 2011). In saying that, it could be that some wages are set at the national level and are not tailored to local economic conditions. For example, some large firms which employ workers across multiple regions of Australia can pay geographically uniform wages. The minimum wage and Australia's detailed system of award wages also apply uniformly across regions, and as such are largely set in response to conditions in the national labour market. All else being equal, this would imply that regional estimates of the wage Phillips curve underestimate the strength of the wages growth–unemployment relationship at the national level.

To explore this, we looked at whether the regional Phillips curve is flatter in regions where a larger share of wages are set at the national level, rather than locally. While we do not have a reliable measure of nationally-set wages, as a proxy we use the estimated share of employees whose wage is set according to an award, based on the region's industrial mix of employment and data on rates of award reliance by industry at the national level. We then take Equation (3) and add an interaction between this ‘award share’ variable and the local unemployment rate. The coefficient of interest is the coefficient on the interaction term, which tells us whether the Phillips curve slope is different between regions that have a larger share of their wages set according to awards, rather than local conditions, vis-à-vis regions with less award reliance. We find the coefficient on this interaction term in the linear model is positive and statistically significant, suggesting that the regional Phillips curve is flatter in regions with a larger award share.^[40] However, this is a very rough proxy for the prevalence of nationally-set wages in a region, because ‘award share’ is not a direct measure of award reliance in the region and because award reliance is only one way that wages can be set nationally.

Exploring this issue in further detail using linked employee–employer data would be a fruitful area for future research. Alternatively, we could simply concede that a bias from nationally-set wages probably does exist, and apply a scaling factor to correct for it. Again, Hazell et al's (2020) theoretical model provides guidance here. It implies that the slope of the Phillips curve estimated using regional consumer prices (capturing both tradeables and non tradeables) is smaller than the slope of the aggregate Phillips curve, by a factor equal to the expenditure share on non-tradeable goods. If we carry this intuition across to the case of the wage Phillips curve, and if we think that, say, 70 per cent of all wages in Australia are set at the local rather than national level, this implies that our regional estimate needs to be scaled up by a factor of around 1.4 (= 1 / 0.7).

7.2.2 Labour mobility

Another challenge of estimating Phillips curves using regional data is that workers can migrate to different regions within Australia to improve their wages or job prospects. Standard theory suggests that a positive demand shock in a local labour market will raise local wages relative to other regions, thus encouraging workers to move in from those regions. If labour is highly mobile in this way, it could potentially complicate inferences about the aggregate Phillips curve based on regional regressions.

Theory does not provide a strong guide in this case. Leading papers that use regional variation to estimate Phillips curves generally assume that labour is immobile across regions, in both their theoretical models and empirical analyses (Hazell et al 2020; Fitzgerald et al 2020). What is clear, however, is that labour migration is an adjustment mechanism for reducing differentials in labour market conditions across regions.^[41] In the absence of any rigorous theoretical guidance, we treat this adjustment mechanism as a factor that reduces the dispersion in unemployment rates across regions, but not one that influences the relationship between unemployment rates and wages growth. In other words, we assume that labour migration reduces the precision of our estimation (by reducing the extent of cross-sectional variation) but is not a key source of bias. In any case, although slow-moving forces such as migration and labour mobility are important for pinning down the precise location of the Phillips curve (via unobservables such as the NAIRU), they should be less relevant for identifying of the slope of the curve itself (which in theory relies on shorter-term business cycle variation).

7.2.3 Persistence in unemployment fluctuations

Due to data limitations, regional Phillips curve studies (including ours) generally do not control for changes in short-run inflation expectations at the region level. In contrast, most aggregate studies of the Phillips curve (particularly those in the United States) do control for short-run inflation expectations. Hazell et al (2020) argue that this difference has implications for the interpretation of regional estimates of the Phillips curve, particularly if fluctuations in unemployment are persistent.

The logic is as follows. It is widely understood that unemployment is a persistent variable. So, if a region faces an idiosyncratic demand shock that pushes its unemployment rate up, people expect it will take several years for unemployment to fall back to pre-shock levels. As a result, they expect the region's inflation rate to be lower in the short term (compared to the no-shock baseline) due to the regional Phillips curve, so they revise down their expectations for inflation in the short run. In turn, this leads to lower actual inflation as predicted by a rational expectations model of the Phillips curve. It follows that, in the absence of controls for short-term expectations, regional estimates can overstate the true slope of the Phillips curve because the observed variation in inflation will reflect not only contemporaneous unemployment, but also an additional anticipatory effect. In contrast, time series estimates that control for short-term inflation expectations will ‘partial out’ the latter effect, and, as a result, the estimated coefficient on contemporaneous unemployment should only reflect the effect of current unemployment on current inflation. Hazell et al argue that this can help account for why regional studies tend to estimate steeper Phillips curves than aggregate studies.

Hazell et al (2020) also propose an estimation approach, consistent with their theoretical framework, which provides a way to account for persistence in unemployment fluctuations in a regional regression. We explain and implement this approach in Appendix D. In brief, we find that the slope of the linear wage Phillips curve is flatter – by a factor of 2 – when we account for unemployment persistence. Following the logic of Hazell et al, this suggests that our baseline estimates of the slope of the wage Phillips curve should not necessarily be interpreted as the true slope of the New Keynesian wage Phillips curve (a structural parameter), unless we scale them down by an appropriate amount (2). Rather, our baseline estimates of the slope of the Phillips curve will capture not only the effects of current unemployment on current wages growth, but also any additional effects that come about through the influence of current unemployment rates on short-run inflation expectations.

It should be noted that, unlike much of the US literature, the RBA's Phillips curve models control for long-run inflation expectations.^[42] However, like our regional specifications, they also omit an explicit control for short-run inflation expectations. As such, all else being equal, our regional approach and the aggregate RBA wage Phillips curve model should (roughly speaking) be identifying the same slope parameter. In that sense, while neither approach can be directly interpreted as the slope of the New Keynesian wage Phillips curve, it makes sense to compare our estimates with those from the RBA's aggregate wages model as we do in Section 7.1

Footnotes

The annualised estimated coefficient is –1.9. [38]

As we discuss in Section 9, the findings of our analysis were incorporated into in the forecast scenarios for wage and price inflation presented in RBA (2021b). [39]

The coefficients on the unemployment rate and interaction terms are –2.83 (0.658) and 0.13 (0.031), respectively (standard errors in parentheses). These estimates suggest that a region that moves from the 25th to 75th percentile of the distribution of ‘award share’ would see the slope of its regional Phillips curve flatten from –0.37 to –0.17. [40]

Debelle and Vickery (1998) find that migration does play a role in equalising labour market conditions between states, although the process takes some time. The Productivity Commission (2014) found evidence that workers move across local labour markets in response to differentials in wage and unemployment rates, but the effects are not large, especially when applied to the typical population gross flows. In 2016/17, only 3½ per cent of households moved more than 50 kilometres from their previous address (Lowe 2018). Survey data suggest that less than 40 per cent of those moves were for work-related reasons, with family, housing or other personal reasons being more important factors (Productivity Commission 2014, Figure 5.9). [41]

The ‘trend’ expectations variable employed in the RBA models uses a range of short- and long-term market- and survey-based measures to extract a common signal of long-term inflation expectations, after controlling for each measure's co-movements with recent inflation (see Cusbert (2017) and Cassidy et al (2019)). [42]