RDP 2018-09: Identifying Repo Market Microstructure from Securities Transactions Data 2. The Repo-detection Algorithm
August 2018
- Download the Paper 2.7MB
The algorithm detects groups of securities transactions that appear to comprise a repo, that is, that satisfy a set of characteristics that repos are assumed to have. Transactions not in these groups are assumed to occur for other reasons. The following information about each transaction is required:
- Settlement time: the day and time the transaction took place.[6]
- Counterparties: CSD account IDs for the securities sender and the securities receiver.
- International securities identification number (ISIN): the type of securities transferred.
- Face value (FV): the face value of securities transferred.
- Consideration: the amount of money, if any, transferred in the opposite direction to the securities.
The key idea is similar to that of the Furfine algorithm, which identifies pairs of payments that are consistent with a loan principal transferred in one direction, then a principal and interest repayment transferred together in the opposite direction the next day. Furfine-type algorithms rely on the unsecured market convention that loans are made in multiples of, for example, $100,000. This convention is not, however, followed in the Australian repo market. Nonetheless, by utilising a larger set of information, that is, including ISINs and FVs, a repo-detection algorithm can still effectively identify repo transactions. Relative to Furfine-type algorithms, the difference in market conventions implies that the repo-detection algorithm must treat more transactions as potential loan initiations, but the ISIN and FV information reduces the number of subsequent transactions that potentially form a repo with any loan-initiation transaction. The net effect is that the computational load remains feasible.
The repo-detection algorithm also detects loans comprising more than two transactions, in contrast to most Furfine-type algorithms that only search for payment pairs. Multiple transaction loans occur if the lender increases the loan size before it is repaid, or the borrower repays the loan in multiple instalments, or there is a collateral top-up or drawdown, or any combination of these happens. Such loans would be missed by an algorithm detecting only transaction pairs. Brassil et al (2016) show that these multiple-transaction loans occur frequently in the unsecured market. In Section 3.2, I show that multiple-transaction repos also occur, but are less common than two-transaction repos.
2.1 Underlying Assumptions
The repo-detection algorithm can be characterised as a collection of conditions that maps a set of securities transactions into a set of ‘detected repos’. The conditions have three parameters: maturity cap, determining the maximum maturity of detected repos, measured in whole days; interest bounds, determining the minimum and maximum annualised simple interest rates that detected repos can have; and transaction cap, determining the maximum number of transactions that can comprise a detected repo.
The conditions that together define a set of transactions as a ‘detected repo’ are:
C1. All transactions occur within an interval of days not greater than maturity cap.
C2. All transactions take place between the same two CSD accounts.
C3. All transactions involve movement of securities with the same ISIN.
C4. The implied simple interest rate from all cash movements in the set is in the interest bounds.
C5. The set involves a net-zero transfer of securities; that is, the FV of securities provided as collateral equals the FV returned.
C6. At no point does the lender return more securities than it has received.
C7. The number of transactions in the set is not more than the transaction cap.
C8. If there exist overlapping sets satisfying C1 to C7, sets with fewer transactions are retained over other sets they overlap with.
C9. If C8 does not remove all overlapping sets (i.e. overlapping sets have equally few transactions), remaining overlaps are in some cases removed by favouring sets with the shortest implied maturity, or by otherwise choosing arbitrarily.[7]
C1 to C5 capture the key assumed characteristics of a short-term repo – opposing transactions between the same accounts within a short period of time, with cash and securities movements consistent with a loan and its collateral. C6 and C7 impose realistic bounds on detected repos that serve to reduce false detections and the required computing capacity.
C8 and C9 handle situations in which a transaction appears in multiple sets that each appear to be a repo. Sets with characteristics that repos tend to satisfy are favoured. Fewer-transaction sets are favoured first, and, in some cases, sets with shorter implied maturities are favoured next. If there still remain overlapping sets, for example, with equally few transactions and equally short maturities, a set is selected arbitrarily, given that the remaining sets are close enough to have little consequence for the dataset of detected repos.
2.2 How the Algorithm Works and the Subset Sums Problem
The process for detecting a two-transaction repo involves first selecting a ‘focus transaction’ – a transaction to treat as a potential loan initiation – then checking whether any subsequent transaction in the dataset pairwise satisfies C1 to C5 with the focus transaction. In contrast, for multiple-transaction repos, C4 and C5 do not permit subsequent transactions to be checked individually; each possible combination of subsequent transactions must be checked as a set. This heavily increases the required computing capacity – a single focus transaction with, for example, 20 potential subsequent transactions, gives over a million possible combinations.[8] Accordingly, it is important to comprehensively narrow down the number of potential transactions before applying C4 and C5, and then to apply C4 and C5 using an efficient method. The relative efficiency of different methods is in part determined by the programming language used – the algorithm presented here is written in R.
For multiple-transaction repos, a focus transaction is selected, then a ‘candidate vector’ is formed of all other transactions that satisfy C1, C2 and C3. The candidate vector is then trimmed by applying C6. Next, all subsets of the candidate vector are checked against C5. Detecting subsets with zero net FV movement is a case of the ‘subset sums problem’, familiar to computer scientists. I combine two methods to solve the problem, implemented in R: first, a matrix-algebra method that checks subsets of limited size (bound above by computing capacity), then, if unsuccessful, an iterative method that checks larger subsets. The relative speed of each method can depend on computer specifications.[9] The user decides the workload allocated to each method by specifying a ‘matrix max’ parameter, which determines the maximum subset size to check with the matrix-algebra method.[10] Subsets satisfying C5 are then screened against C4, C6 and C7, and overlaps removed by applying C8 and C9.
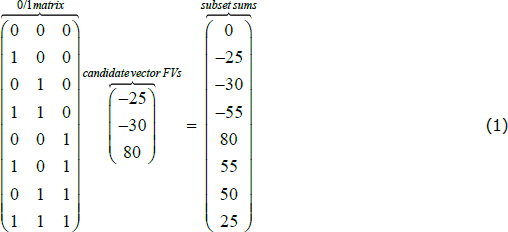
The matrix-algebra method is illustrated in Equation (1). First, elements of the candidate vector of FVs are made negative if the transactions are in the same direction to the focus transaction. Then this vector of FVs is pre-multiplied by a matrix of 0s and 1s that represents all possible subsets, and the result is a vector of subset sums that can be checked for values equalling the focus transaction FV. The 0/1 matrix has a column for each transaction in the candidate vector, and a row for every possible subset, with 1s where the corresponding candidate element is present in that subset. In Equation (1), if the focus transaction FV is 50 and the candidate vector FVs are (−25, −30, 80), the subset represented by the (0, 1, 1) row of the 0/1 matrix is a candidate subset, because the corresponding element of the subset sums vector equals 50.
The 0/1 matrix can be quickly generated using the base R ‘expand.grid’ function, although its size exceeds memory limits for long candidate vectors. For the applications in this paper and the computing resources available, the maximum achievable length is 22. Matrix max can be set no higher than this maximum. For candidate vectors longer than matrix max, the vector is trimmed to matrix max length by excluding transactions furthest in time from the focus transaction, and then checked using the matrix-algebra method.
If a repo is not detected by the matrix-algebra method I then use an approach that can accommodate longer candidate vectors. The full candidate vector is trimmed to a longer threshold, determined by computing capacity (45 in this paper), prioritising transactions closest in time to the focus transaction. This vector is then checked using an ‘iterative’ method. Denoting the transaction cap in C7 as K, the method iterates through k = 1, …, K − 1, using the base R ‘combn’ function to construct each possible combination of k candidate vector elements, and checking their FV sums. For each k, this method is similar to applying the matrix-algebra method on the subset of the 0/1 matrix that contains only rows with k non-zero elements. For example, for k = 1 these are the rows that form the identity matrix. If there are candidate vectors longer than this higher threshold, the computing constraints result in unchecked potential combinations. Section 3.2 assesses the consequences of this.
2.3 The Algorithm Procedure
Before running the algorithm, any transactions involving the RBA or ASX are removed. Detected intraday repos, defined as two transactions on the same day with the same ISIN, FV and consideration, and in opposite directions between the same two accounts, are also removed. This assumes an intraday interest rate of zero, consistent with intraday repos on offer from the RBA, although other assumptions on intraday interest rates or fees can easily be imposed.[11]
For two-transaction repos, the process is essentially:
Step 1.1 Select a transaction as the ‘focus transaction’.
1.2 Find all other transactions that satisfy C1 to C5 pairwise with the focus transaction (if any). Store the pairs.[12]
1.3 Repeat 1.1 and 1.2, treating every transaction in the dataset as a focus transaction. Store all pairs.
1.4 Sort all the stored pairs by increasing maturity, measured in days, with equal maturities ordered arbitrarily.
1.5 Define the first pair in the sorted list as a detected repo, remove from the list any subsequent pairs that it overlaps, and repeat down to the bottom of the list of pairs.
Transactions in detected two-transaction repos are then removed and the remaining transactions are checked for multiple-transaction repos. The process is essentially:
Step 2.1 Select a transaction as the ‘focus transaction’.
2.2 Find all other transactions that satisfy C1 to C3 pairwise with the focus transaction. Store these together in a ‘candidate vector’ that is linked to the focus transaction.
2.3 Remove transactions from the candidate vector that would violate C6 in any combination.
2.4 Repeat 2.1 to 2.3, treating all transactions as a focus transaction, and collect all candidate vectors.
2.5 Define a temporary maximum number of transactions, starting with three.
2.6 Select a candidate vector. Remove any transactions in already-defined detected repos.
2.7 Find subsets of the candidate vector with FVs summing to the focus-transaction FV using the methods discussed in Section 2.2, after making the FVs of transactions in the same direction as the focus transaction negative. Remove subsets not satisfying C4 or exceeding the temporary maximum number of transactions. If multiple remain, keep only the minimum-maturity subsets (measured as nights between first and last transaction), and if multiple still remain, arbitrarily select one. Define it as a detected repo.[13]
2.8 Repeat 2.6 and 2.7, working through every candidate vector.
2.9 Increase the maximum transaction number specified in 0 by one, repeat 2.6 to 2.8, and then repeat until the transaction cap is reached.[14]
The online supplementary information contains the R code with explanations included as comments.
Footnotes
With minor modifications the algorithm would work if only the settlement day is observable, but would have more difficulty detecting some repos that involve more than one transaction on the same day. [6]
In some cases, longer-maturity sets may be selected over others because the crosschecking required would substantially increase computing time. This could be modified if computing capacity imposed less constraint. [7]
The number of possible combinations among N transactions is 2N. [8]
Modifications of the standard dynamic programming solution to the subset sums problem were found to be inefficient in this setting. [9]
In the code in the online supplementary information, this parameter is the ‘matrix.max’ argument in the top-level ‘repo.alg.F’ function. [10]
There is little evidence in the data that intraday repos occur at other interest rates or with a fixed fee. [11]
In practice, only the locations (e.g. row numbers) of transactions are stored. [12]
Alternatively, it would be straightforward to choose from overlapping repos using other characteristics such as implied interest rate or settlement times. [13]
For each temporary maximum transaction number, it is not necessary to iterate through the lower values of k referred to in the above description of the iterative method. However, the improvements in computing time from removing these iterations are small, and additional detections are possible given the constraints imposed on candidate vector lengths. [14]