RDP 2018-09: Identifying Repo Market Microstructure from Securities Transactions Data 4. Comparing the Output with Prudential Data
August 2018
- Download the Paper 2.7MB
The RBA analyses partially aggregated data on repo positions collected by the Australian Prudential Regulation Authority (APRA).[27] Registered financial corporations (RFCs) with assets above $500 million and Australian-licensed authorised deposit-taking institutions (ADIs) provide quarterly reports of repo and securities-lending positions held on their domestic books. They report the value of aggregate positions per counterparty type per collateral type, separately for borrowing and lending positions. There are twelve counterparty types, one being the RBA, and four collateral types, comprising AGS, SGS, other debt and equities. For example, 1 of the 96 figures in each entity's quarterly report is lending positions to non-resident counterparties against AGS collateral.
The APRA data generate two aggregated series – repo lending by reporting entities and repo borrowing by reporting entities (excluding from the RBA). The difference between these reflects net lending from reporting entities to non-reporting entities such as foreign institutions. The algorithm data can be compared to these series by aggregating detected repos that are open at September ends (Figure 3).[28] These algorithm and APRA series display broadly similar trends for AGS and SGS repos. However, the algorithm positions are smaller than the quantities reported to APRA, more so for the APRA lending series. There are several likely reasons. For repos against ‘other debt’, the difference would include any repos against discount securities, which are not in the transactions dataset I analyse and therefore not detected by the algorithm.
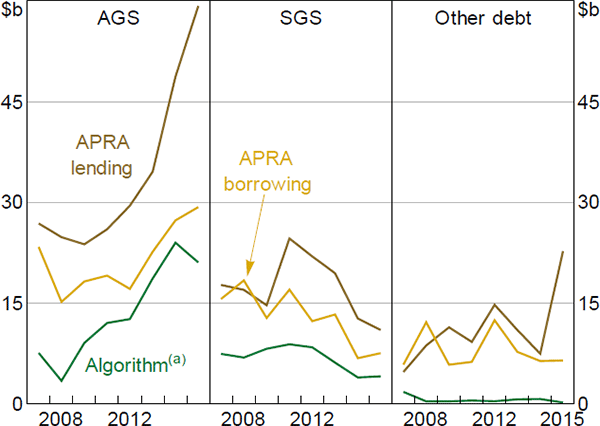
Notes:
Austraclear sample years are 2006, 2008, 2009, 2010, 2012, 2013, 2014 and 2015
(a) Algorithm run with 61-day maturity cap
Sources: APRA; ASX; Author's calculations; RBA
For AGS and SGS collateral, the difference likely reflects repos transacted through infrastructure other than Austraclear. Two ICSDs – Euroclear and Clearstream – enable their participants to transact Australian dollar-denominated securities that are ultimately held in Austraclear, but without transactions between Austraclear accounts taking place. The securities are held by a nominee with an Austraclear account on behalf of the ICSD, and the ICSD holds them on behalf of its participants. When the ICSD participants transact with each other the ICSD changes its own records of the securities' ownership but, in Austraclear, the securities remain in the nominee's account. Since the ICSDs have no direct link to RITS, any Australian-dollar cash settled simultaneously with these transactions takes place across accounts at a private bank employed by the ICSD.
This reason for the difference across data sources – the APRA data capturing repos settled through foreign infrastructure – is consistent with the algorithm figures being closer to the APRA borrowing figures than the APRA lending figures (Figure 3). Recall that the gap between the APRA lending and borrowing series reflects net lending from entities that report to APRA to entities that do not. Becker and Rickards (2017) attribute a substantial part of this net lending to demand from non-residents for Australian dollar repo funding as part of international arbitrage positions. Since non-residents are more likely to hold ICSD accounts than Austraclear accounts, it seems likely that these lending positions would not appear in the algorithm data.
There are several more reasons why repos could be reported to APRA but not appear in the algorithm data. First, like repos through ICSDs, other repos could occur within a single Austraclear account (thus, without any Austraclear transactions), if they are between counterparties that are part of the same company, between two clients of the same Austraclear participant, or between an Austraclear participant and one of its clients. Second, repos would be absent from these algorithm data if any of their transactions occur before or after the two-month transaction sample ends. This is likely for repos open longer than a month and definite for repos open longer than two months. Third, repos involving Australian dollar-denominated securities but foreign currency would not be detected because the cash side would not appear in the Austraclear data. Fourth, securities loans are reported to APRA but, if the interest rate is below the interest bounds, they would not be detected by the algorithm. This is plausible given what is known about securities lending markets. Finally, repos initiated on the same day between the same counterparties and involving the same ISIN can be bilaterally netted before being transacted in Austraclear, but the gross positions may still be reported to APRA. It is also possible that repos reported to APRA are netted against trades in the underlying securities before being transacted in Austraclear.
To more formally compare the datasets, I regress APRA observations on corresponding algorithm observations, similar to the approach by Kovner and Skeie (2013). Three levels of data aggregation are considered: an observation per entity per year per collateral type; an observation per entity per collateral type (i.e. aggregated across years); and an observation per year per collateral type (i.e. aggregated across entities). To better align the datasets, entities whose APRA-data and Austraclear-account IDs cannot be closely matched are removed. The algorithm is run with a maturity cap of 61 days, and the APRA observations exclude positions held with counterparties other than banks, RFCs, other ADIs and non-residents.
Table 6 reports the estimates. Regression exogeneity assumptions could feasibly be violated, so the estimates and significance levels should be interpreted with some caution. Notwithstanding this, in all specifications the estimated slope coefficients indicate a statistically significant positive relationship between the algorithm and APRA data, denoted by the asterisks on the right of the coefficients. The datasets are clearly positively related. Given this, I also test the hypothesis that the two datasets move one-for-one, that is, that the slope coefficient equals one, with significance denoted by the asterisks to the left of the coefficient estimates. In only one case is this hypothesis not rejected. Loosely speaking, the APRA lending figures tend to vary more than the algorithm figures (i.e. coefficients greater than one), and the APRA borrowing figures tend to vary less (i.e. coefficients less than one). Correlations between the two datasets vary between 0.4 and 0.9, with little discernible difference for the APRA lending and borrowing datasets. This similarity in correlations may indicate that repo activity through Austraclear is correlated with repo activity through other infrastructure.
| Entity and year level | Entity level | Year level | ||||||
|---|---|---|---|---|---|---|---|---|
| Lending | Borrowing | Lending | Borrowing | Lending | Borrowing | |||
| Intercept | 0.533*** (0.07) |
0.440*** (0.05) |
1.382** (0.55) |
1.618*** (0.34) |
5.178*** (0.89) |
3.779*** (0.70) |
||
| Slope | ***1.452*** (0.16) |
***0.519*** (0.07) |
***2.487*** (0.32) |
**0.757*** (0.11) |
***2.056*** (0.22) |
0.983*** (0.13) |
||
| Correlation | 0.45 | 0.41 | 0.69 | 0.65 | 0.90 | 0.85 | ||
| R squared | 0.21 | 0.17 | 0.47 | 0.43 | 0.80 | 0.73 | ||
| Sample size | 309 | 304 | 69 | 69 | 24 | 24 | ||
|
Notes: **p < 0.05, ***p < 0.01; asterisks on the left of slope coefficients test whether coefficients equal one; OLS standard errors in parentheses Sources: APRA; ASX; Author's calculations; RBA |
||||||||
Unfortunately it is not possible to precisely account for each difference between the APRA and algorithm data, which must be kept in mind for the analysis in Section 5. Nevertheless, there is widespread ownership of Austraclear accounts across entities active in the Australian financial system (including many related to branches and subsidiaries of foreign banks). These entities have some incentive to use Austraclear rather than ICSDs owing to Austraclear's ability to simultaneously settle securities against domestic central bank currency. Moreover, for AGS and SGS repos, the algorithm and APRA series display similar trends across time. Taking everything into account, it seems reasonable to interpret the algorithm data as capturing the short-term domestic interbank repo market, acknowledging that this omits repos transacted through foreign infrastructure. This corresponds to the typical definition of the Australian unsecured interbank market, which only includes loans that are transacted through RITS.
Footnotes
The APRA dataset in more aggregated form can be found in statistical table B3 ‘Repurchase Agreements and Stock Lending by Banks and Registered Financial Corporations’ at <https://www.rba.gov.au/statistics/tables/>. [27]
For this section I set the maturity cap at 61 days, the interest bounds at 1 percentage point either side of each window's cash rate range, and the transaction cap at 6. I use the longer maturity cap because repos of all maturities are reported to APRA. [28]