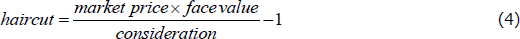RDP 2018-09: Identifying Repo Market Microstructure from Securities Transactions Data 5. The Australian Repo Market Microstructure
August 2018
- Download the Paper 2.7MB
Now that we have a database of repo market transactions that is confirmed to be reasonably accurate, I examine the repo market microstructure implied by these data. The data cover the segment of the short-term (i.e. two weeks or less) repo market that is transacted through Austraclear. As discussed in Section 4, it seems reasonable to view this segment as the domestic interbank market, loosely defining all financial institutions as banks, and excluding from this definition repos involving banks with little presence in Australia. By comparison, previous published RBA analysis of the repo market adopts a broader scope more in line with activity reported to APRA. It is also worth reminding readers that the data in this section cover windows of September and October, which may not be representative of repo activity in other parts of the year, although the APRA data do not indicate much quarter-on-quarter volatility. Notwithstanding, there is some evidence that activity in short-term repos declines at quarter ends. On average, the value of detected repos outstanding declines 10 per cent in the two weeks encompassing each quarter end, relative to the value of detected repos the week before and the week after these two weeks.
In the following analysis, detected repos with particular characteristics are sometimes excluded to reduce the potential influence of false positives or of repos that are not representative of the information being conveyed. For example, when analysing spreads to the cash rate, repos open across the night after RBA Board meetings are typically excluded, because reference rates used by repo counterparties may diverge from the cash rate in those periods. Also, multiple-transaction repos are excluded where a small number of false positives could skew the information provided.[29]
As mentioned in the Introduction, the algorithm data treat securities loans – sometimes referred to as special repos – as a subset of repos. As opposed to ‘general collateral (GC) repos’, which are driven by the securities provider's demand for cash, securities loans are driven by the securities receiver's demand for the specific collateral. The securities receiver may, for example, be using the security to cover a short sale or to temporarily increase its inventories. In Australia, securities borrowers typically provide cash to collateralise the securities loan, which makes their transactions difficult to distinguish from other types of repos. This distinction can also be difficult conceptually, because there is likely some element of demand for cash in a typical securities loan, and of demand for the securities received in a GC repo. Throughout the following analysis the term ‘repo’ includes securities loans to the extent they satisfy the interest rate bounds, and ‘lender’ and ‘borrower’ always refer to the provider and receiver of cash (respectively).
5.1 Market Size, Collateral Types, Interest Rates and Maturities
The algorithm data reveal many repo characteristics not observable in previously available datasets. This section starts by describing the aggregate detected market, then analyses distributions of important variables such as collateral types, maturities (measured as number of days open) and interest rates. This informs us about, for example, the role that certain types of securities perform in our financial system, and the degree to which monetary policy transmits into other interbank rates.
Between 2006 and 2015 the market size grew from around $5 billion to around $12 billion, measured by the value of outstanding positions on a typical night (Figure 4). In 2008, the SGS repo market was larger than the AGS repo market. Garvin, Hughes and Peydró (forthcoming) show that the repo market expanded substantially during the 2008 window, which captures the period surrounding the Lehman Brothers collapse, and the growth was primarily in SGS repos. They attribute this to increased demand for repo alongside a relative scarcity of AGS. In later years the proportion of the market against SGS declined, and in 2015 was less than a tenth the size of the AGS repo market. Throughout the full sample there is relatively little activity in repos against other-debt collateral, although any repos against privately-issued discount securities would not be captured (see Section 4).
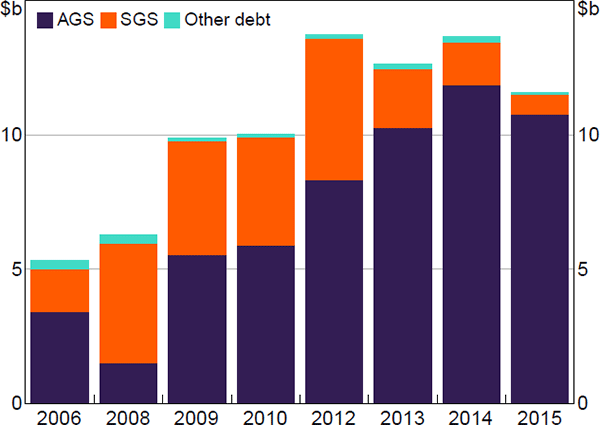
Notes: September and October only; algorithm run with 14-day maturity cap; averaged across all nights excluding first and last two weeks each window
Sources: ASX; Author's calculations
Table 7 reports the ten issuers whose debt securities are most commonly used as repo collateral, and how many repo counterparties (i.e. number of Austraclear accounts) use that collateral. Aside from the Australian Government, the most prevalent issuers are the Queensland and NSW state governments, followed by the Victorian and Western Australian state governments. The most used other-debt collateral is issued by two supranationals and two German development banks. Collateral types tend to be broadly accepted – all in the table are provided by at least 16 different borrowers and accepted by at least 16 different lenders, with higher numbers for the more prevalent types. Two private sector entities rank twelfth and thirteenth (not shown in the table) with around 50 detected repos each.
Focusing on the 2015 window, the market does not appear to concentrate in particular ISINs within the AGS category of collateral (Table 8). Of the 32 ISINs on issue at some point in the window, all bonds and all but 1 treasury note appear in repos at least once. Each (non-indexed) treasury bond ISIN is used in at least 6 repos and each treasury indexed bond ISIN is used in at least 16 repos. Treasury bond ISINs tend to be favoured over other AGS ISINs, likely related to their long tenor and the large quantity on issue.
| Issuer | Detected repos | Borrowers | Lenders |
|---|---|---|---|
| Australian Government | 15,879 | 59 | 62 |
| Queensland Treasury Corporation | 2,894 | 48 | 54 |
| New South Wales Treasury Corporation | 2,278 | 48 | 51 |
| Treasury Corporation of Victoria | 859 | 40 | 45 |
| Western Australian Treasury Corporation | 849 | 47 | 43 |
| European Investment Bank | 309 | 29 | 32 |
| KFW Banking Group (Germany) | 271 | 27 | 28 |
| South Australian Financing Authority | 170 | 26 | 36 |
| Landwirtschaftliche Rentenbank (Germany) | 119 | 21 | 22 |
| International Bank for Reconstruction and Development | 79 | 16 | 16 |
|
Note: Algorithm run with 14-day maturity cap Sources: ASX; Author's calculations |
|||
| Treasury bonds | Treasury indexed bonds | Treasury notes | |
|---|---|---|---|
| Number of ISINs on issue | 22 | 7 | 3 |
| Lowest frequency of an ISIN | 6 | 16 | 0 |
| Median ISIN frequency | 121 | 30 | 3 |
| Highest frequency of an ISIN | 213 | 37 | 4 |
|
Notes: Algorithm run with 14-day maturity cap; repos with more than two transactions excluded Sources: ASX; Author's calculations |
|||
Figure 5 plots the interest rate spread to the cash rate for every repo, excluding those open across RBA policy decisions. The position on the x-axis represents the business day and time the first transaction in the repo was settled. For example, a point in the 2015 panel at (20.5, –10) would represent a repo 20.5 business days into the 2015 September–October window – that is, at 12 pm on the 21st day – at 10 basis points below the cash rate. When plotted observations overlap they may not all be visible in the figure; the layering from least visible to most visible reflects their frequency – AGS, SGS, then other-debt collateral.
At each point in time rates tend to be dispersed in a 50 basis point range, even within collateral types. The cross-sectional variance overshadows the market-wide variance across days, although the distribution of spreads tightens from 2006 to 2015. This could relate to, for example, a shift towards shorter maturities, discussed later in this section, a change in the dispersion of loan sizes, or changes in the role of the market. Spreads tend to be concentrated at multiples of 5 basis points, indicating common use of the cash rate as a reference rate.
Around 42 per cent of the positive spreads in Figure 5 are overnight repos, which suggests that access by these borrowers (i.e. cash receivers) to the unsecured market was constrained; otherwise they would borrow unsecured at a lower rate and without any collateral obligation. There is also a cluster of repos at 25 basis points below the cash rate. These repos are likely securities loans, consistent with the relatively high frequency of non-government collateral.[30] Market intelligence also indicates that rates on securities loans are sometimes negotiated from a reference point of 25 basis points below the cash rate.
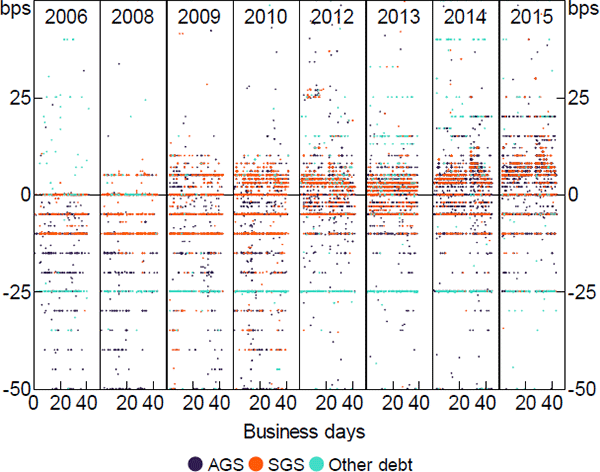
Notes: September and October only; algorithm run with 14-day maturity cap; repos spanning policy decisions excluded
Sources: ASX; Author's calculations; RBA
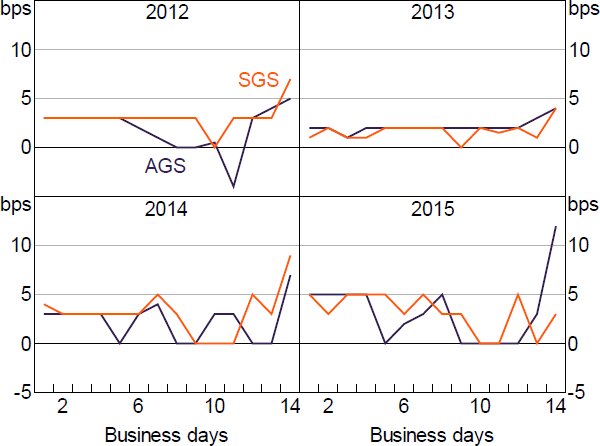
Figure 6 plots the pattern of increasing spreads evident in Figure 5, displaying the median spread each year for AGS and SGS repos. Becker, Fang and Wang (2016) and Becker and Rickards (2017) also note increasing market-wide repo rates towards the end of this sample, finding evidence that demand for Australian dollar funds from non-resident borrowers has been contributing to these rises. A noticeable deviation between AGS and SGS spreads occurs in 2008. Garvin et al (forthcoming) conclude that this is at least partly driven by demand for AGS (i.e. the highest quality collateral) alongside a relative scarcity on issue.
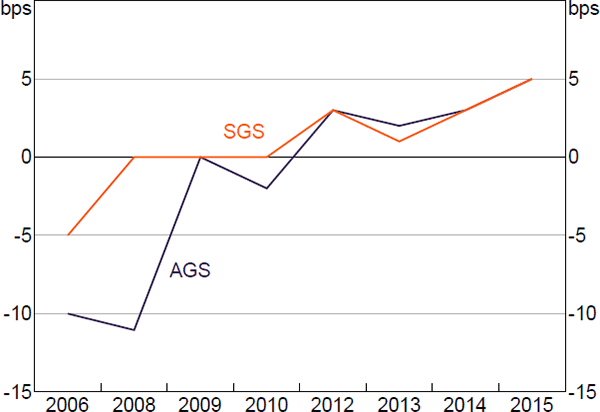
Notes: September and October only; algorithm run with 14-day maturity cap; repos spanning policy decisions excluded; one high turnover borrower-lender pair excluded
Sources: ASX; Author's calculations; RBA
For maturities of 14 days or less, there is little evidence of a yield curve (Figure 7). Only repos with rounded interest rates are displayed, because these are more likely to have terms negotiated at the start of the repo rather than being rolled over, and therefore the time between the first and last transactions is more likely to represent overall maturity rather than the sum of several rolled over maturities.[31] Spreads for 1-, 2- and 3-day maturities tend to be relatively flat, and spreads at 14 days tend to tick up. Nevertheless, there is no clear systematic trend evident.
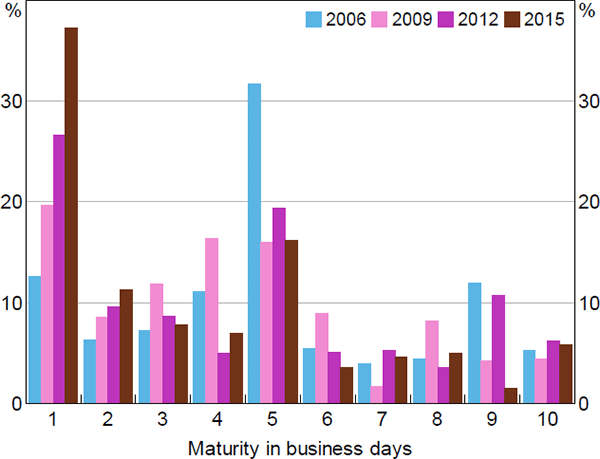
Figure 8 defines maturity as business nights between the first and last transaction, excludes repos most likely to be rollovers, and displays the market share at each maturity. Between 2006 and 2015 the market shifts towards overnight maturities. In all displayed years there is substantial market share at one-week maturity (i.e. five business days); however, this declines from around 30 per cent in 2006 to be below 25 per cent in every subsequent year in the sample (including those not displayed). Excluded from Figure 8 is a borrower-lender pair that in 2015 contributes a disproportionate share of turnover; including them makes the overnight market share above 50 per cent.
Notes: September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions, spanning policy decisions or with non-rounded interest rates excluded; one high turnover borrower-lender pair excluded
Sources: ASX; Author's calculations; RBA
Notes: September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions or with non-rounded interest rates excluded; one high turnover borrower-lender pair excluded; averaged across all nights excluding the first and last two weeks of each window
Sources: ASX; Author's calculations
For an indication of whether repos occur at maturities above two weeks, I also run the algorithm with a 61-day maturity cap. For these longer maturity repos, turnover is a more useful measure of activity than share of outstanding positions.[32] In 2006, there is a pronounced spike in turnover detected at 30 days (retaining non-business days) that comprises 12 per cent of total turnover. In 2015, aside from a small spike of around 0.5 per cent of turnover at 21 days, activity at maturities longer than 14 days is scarce.[33]
5.2 Loan-level Regressions of Repo Rates
Next I analyse repo interest rates by regressing them on other repo characteristics. This allows formal tests of whether repo rates vary with other repo characteristics while holding potentially confounding variables constant. Treating each detected repo from 2012 to 2015 as an observation, I regress interest rates on appropriate transformations (specified in Table 9) of the following variables: the quantity of lender's OMO borrowing that morning;[34] the size of the repo (i.e. cash lent); a dummy indicating whether the lender subsequently sold the collateral it received while the repo was still open, indicative of the repo being used to cover a short sale;[35] dummies for maturity buckets; dummies for collateral types; and a dummy indicating whether the collateral was a reference bond in the futures market.[36]
Individual repos are indexed by i, such that the space of i includes dimensions for lender l, borrower b and day d (and therefore also year y), with lender and borrower measured at the CSD account level. The set of explanatory variables is labelled X. I estimate two equations:
and
Equation (2) includes day fixed effects to control for any day-to-day fluctuations in market-wide rates. Equation (3) includes day fixed effects and borrower*lender*year fixed effects, focusing on variance in rates within borrower-lender pairs each year. For example, if a correlation exists among a set of repos that each involve different lenders or borrowers (on the same day), Equation (2) would detect it and Equation (3) would not. Equation (3) excludes rate differentials across different counterparties, focusing on, for example, whether repos between the same two counterparties have higher rates when the loans are larger. Equation (3) is therefore more robust to omitted variable bias driven by unobserved characteristics that vary across counterparties.
Table 9 reports the coefficient estimates. Notable findings are:
- Consideration: Loan size has a highly significant and positive relationship across both specifications. When a loan doubles in size, the rate increases by around 0.8 basis points. Possible explanations could include a thinner market for larger loans that tilts market power towards the lender, or compensation to the lender for a higher concentration of counterparty risk in that borrower.
- Short sale: Repos appearing to cover short sales (likely to be securities loans) have rates 1.3 basis points lower than others. The sign is as expected, with cash providers compensating borrowers for receiving the collateral. The dummy is a proxy and may result in underestimates if it also picks up repos used for other purposes.
- Maturities: The Equation (2) estimates are consistent with a term premium, that is, estimated rates are higher for longer maturity buckets. However, the Equation (3) estimates reveal that this is not true when holding the counterparties constant.
- Collateral type: SGS repos tend to have a rate around 1 basis point higher than AGS repos. Bartolini et al (2011) find a similar but wider disparity in the United States – in data up to 2006, rates on repos against Treasury securities are around 5 basis points lower than rates on repos against agency securities. Other-debt repos tend to have a rate around 6 basis points lower than AGS repos. These repos potentially comprise more securities loans.
- Futures collateral: These repos have statistically significantly higher rates by 0.7 basis points. This is consistent with the arbitrage position discussed in Wakeling and Wilson (2010) and Becker et al (2016). Specifically, banks short futures and buy the underlying bonds to take advantage of the futures price being above the price of the underlying bonds. Banks can fund the bond purchase by borrowing through repos using the bond as collateral, putting upward pressure on rates for these repos.
| Equation (2) | Equation (3) | |
|---|---|---|
| Lender's OMO (IHS, $b)(a) | 4.882 (3.75) |
−0.536 (0.47) |
| Consideration (log $m) | 0.890*** (0.30) |
1.136*** (0.20) |
| Short sale (D) | −2.53 (1.66) |
−1.264** (0.48) |
| Maturity 2–7 days (D) | 1.960* (0.98) |
0.262 (0.33) |
| Maturity 8–14 days (D) | 2.913** (1.21) |
0.132 (0.57) |
| SGS collateral (D) | 1.215** (0.56) |
0.960*** (0.32) |
| Other-debt collateral (D) | −6.136 (4.97) |
−6.189* (3.34) |
| Collateral referenced in futures (D) | 0.596 (0.38) |
0.704*** (0.26) |
| Fixed effects | day | day and borrower*lender*year |
| R squared | 0.081 | 0.471 |
| Number of observations | 15,955 | 15,695 |
|
Notes: *p < 0.1, **p < 0.05, ***p < 0.01; standard errors in parentheses clustered at the lender account level (42 clusters); state government entities removed from regressions; D denotes a dummy variable (a) IHS refers to the inverse hyperbolic sine transformation, similar to a log transformation but capable of transforming zeros Sources: ASX; Author's calculations; RBA |
||
5.3 Market Structure in 2015
In this section I analyse the distribution of counterparty relationships in the repo market. The algorithm data identify the borrower and lender to each position. This permits analysis of: a) the relative activity of each entity; b) the network of repo positions; and c) how repo rates vary across the market network. Since these market characteristics vary over the full sample, I focus on the most recent data window comprising September and October 2015. Note that these data do not capture repos through foreign infrastructure, which could, for example, add extra links to the market network as implied by the algorithm data.
Because institutions often hold multiple Austraclear accounts, for this section I group accounts into ‘entities’, combining activity across any accounts held under the same parent company. The exception is when the account name indicates it is used on behalf of clients, in which case I label that account, grouped together with any other client accounts under the same parent company, as being a client entity.[37] Two of the client entities include accounts related to ICSDs. Entities other than client entities and state governments are classified as domestic or foreign, based on the location of their parent company. Intra-entity repos are excluded.
Figure 9 displays each entity's share of total repo turnover in 2015, measured as the sum of the cash side of all repos in the window regardless of maturity. Each horizontal bar is an entity; the left and right panels display that entity's lending and borrowing turnover respectively. Turnover is highly skewed towards a single borrower-lender pair, contributing around half of the total. Aside from this pair, the bulk of turnover is distributed across 15 to 20 entities, most of whom both lend and borrow. Five of the six most active of these entities are Australian, and most of the remaining activity is by foreign and client entities.
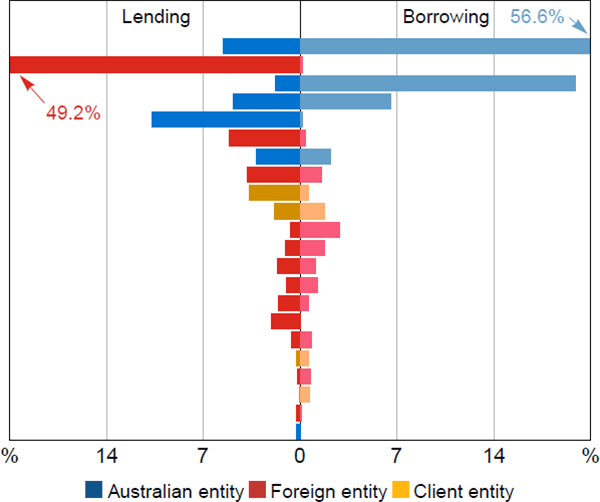
Notes: Algorithm run with 14-day maturity cap; entities ordered by combined borrowing and lending turnover; excludes repos with state government entities
Sources: ASX; Author's calculations
Figure 10 illustrates the market as a network. Each node is an entity, coloured by domicile (or client). The shape represents its average net overnight position across all counterparties – circles are net lenders, squares are net borrowers, and the size of the shape represents the value of their average net overnight position (using a nonlinear scale). Each (undirected) edge represents a bilateral position, with the thickness representing the total gross value of lending and borrowing between that pair (also using a nonlinear scale).
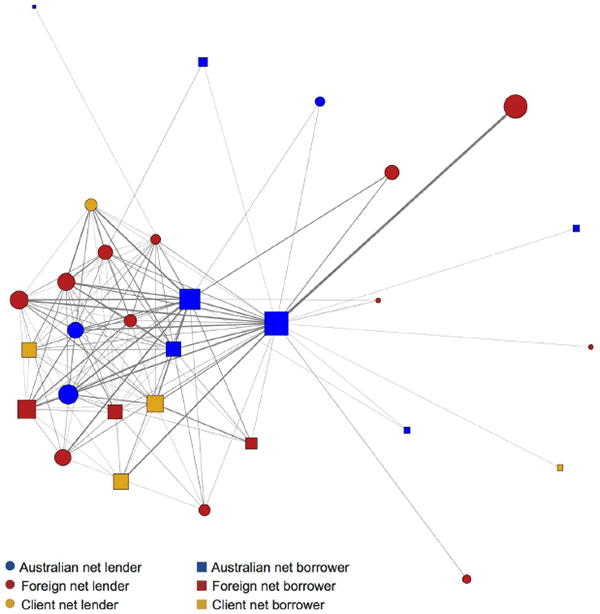
Notes: Node size represents average overnight position netted across all counterparties; edge width represents average gross overnight position between counterparty pair; algorithm run with 14-day maturity cap; excludes repos with state government entities
Sources: ASX; Author's calculations
There is a distinct core-periphery split.[38] Around a third of entities are ‘periphery’ entities that are not linked with each other and have only one or two counterparties. Around two-thirds are ‘core’ entities, each with five or more counterparties in the core, plus counterparties in the periphery. The core is well integrated; most have more than ten counterparties. On the other hand, if data in this sample are representative of the current market structure, periphery entities are somewhat segmented and their market access might easily be disrupted if there are problems with their one or two core counterparties. The market structure seems inconsistent with core entities' primary activity being intermediation for the periphery, given core entities' relatively large net positions. Among the core, the pattern is more consistent with market ‘churn’ related to entities seeking other entities with which to offset day-to-day surpluses and deficits in liquidity and securities holdings.
Repo rates tend to vary across counterparties. Figure 11 plots the estimated difference in rates between different lender and borrower types, with 95 per cent confidence intervals, relative to rates on repos between Australian lenders and Australian borrowers. Specifically, the coefficients are from a re-estimation of Equation (2) on 2015 data with X comprising: eight domicile dummy variables representing the nine types of lender-borrower combinations, with loans from Australian lenders to Australian borrowers as the baseline; dummies for 2–7 and 8–14 day maturity buckets; and dummies for collateral types. Rates are highest for repos from Australian lenders to client borrowers, in line with Becker and Rickards' (2017) explanation that non-residents' demand for funding has put upward pressure on repo rates in recent years. Overall, rates charged by Australian lenders tend to be higher than rates charged by other lenders. The lowest rates are from client lenders to foreign borrowers.
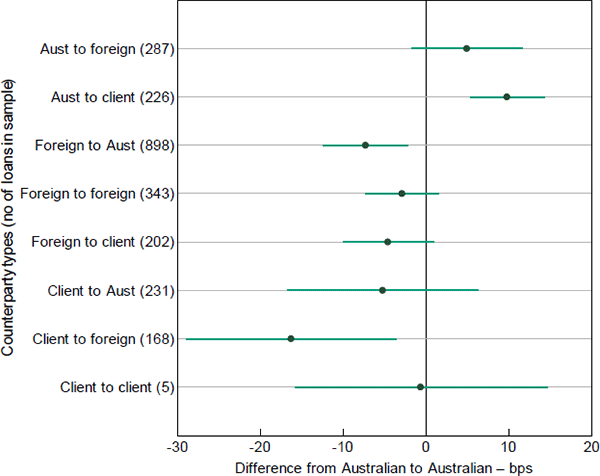
Notes: With day fixed effects and other control variables; clustered standard errors
Sources: ASX; Author's calculations
There is some evidence of collateral rehypothecation in the algorithm data. Potential rehypothecation can be identified as instances of an entity receiving collateral as a lender, then using securities of the same ISIN as collateral for borrowing later on the same day. Around 5 per cent of the two-transaction repos detected are followed by potential rehypothecation (after removing overlapping instances).
5.4 Haircuts
A repo haircut (sometimes called an initial margin) is defined as the proportion by which the collateral value exceeds the cash lent:
Haircuts are intended to keep the lender fully collateralised should the market price of the securities move adversely. The data may therefore inform us about how repo counterparties manage their risk. Under global conventions, haircuts are higher for securities with more volatile prices, which have greater potential to change in price while the repo is open. For current RBA lending in OMO, the lowest haircut is 1 per cent, corresponding to AGS and SGS, and the highest haircut is 20 per cent, corresponding to asset-backed securities. For securities loans (which likely describes some of the detected repos) we may expect haircuts as defined by Equation (4) to be negative. This would protect the securities lender, rather than the provider of the cash collateral, against changes in the securities price.
To obtain implied haircuts from the algorithm repo data, the repo dates and collateral ISINs can be aligned with data on securities market prices. I do this using the (mid) closing prices each settlement day for all AGS and SGS repos in the 2012 to 2015 windows, with data from the RBA and Yieldbroker. For multiple-transaction repos, the implied haircut is measured using only the first transaction. Market intelligence indicates that some repos are negotiated the day before the first-leg settlement, which may result in some misalignment between the repo and securities price data, adding noise to the haircut measure I construct. Notwithstanding this, this measure has lower variance than a measure that uses securities prices from a day earlier.
Implied haircuts tend to be scattered around zero – in each window the mean haircut is less than 0.1 per cent in absolute value (Figure 12). In 2014 and 2015 there are clusters around 1 and 2 per cent, which reflect only a small subset of entities. Implied haircuts are often negative. The negative haircuts are spread across various counterparties, ISINs and settlement times, and, gauged by the incidence of rounded interest rates (discussed in Section 3.3), do not contain a noticeably larger proportion of false positives. These may comprise a higher proportion of securities loans.
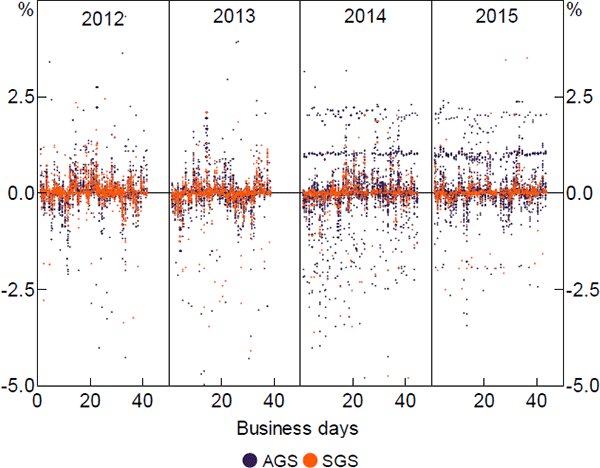
Note: Algorithm run with 14-day maturity cap
Sources: ASX; Author's calculations; RBA; Yieldbroker
To further investigate implied haircut patterns I regress Equations (2) and (3) from Section 5.2 replacing ratei with haircuti and limiting the sample to AGS and SGS repos between 2012 and 2015. I use the same explanatory variables X, but also include the repo rate in basis points. If haircuts represent value to the lender and a cost to the borrower, we may expect a negative relationship with repo rates, as counterparties negotiate by raising one and lowering the other. To lenders, higher haircuts reduce counterparty risk and temporarily increase liquid asset holdings. To borrowers, haircuts may represent the cost of capital for securities financing, being the gap between the funds obtained by borrowing against the security and the funds required to purchase it (e.g. Ashcraft, Gârleanu and Pedersen 2011).
Table 10 reports the estimates. Of the 16 reported coefficients, 1 is significant at 90 per cent confidence, therefore likely a type I error.[39] There is no significant relationship between haircuts and repo rates, indicating they are not simultaneously negotiated. The coefficient on the short sale dummy is also not significant, which is at odds with the notion that the negative haircuts correspond to securities loans.
| Equation (2) | Equation (3) | |
|---|---|---|
| Repo rate (bps) | 0.078 (0.38) |
0.060 (0.08) |
| Lender's OMO (IHS, $b)(a) | 0.014 (0.04) |
0.006 (0.04) |
| Consideration (log $m) | 0.038 (0.03) |
−0.001 (0.00) |
| Short sale (D) | −0.015 (0.03) |
−0.009 (0.01) |
| Maturity 2–7 days (D) | −0.021 (0.05) |
0.026* (0.01) |
| Maturity 8–14 days (D) | −0.011 (0.04) |
0.011 (0.02) |
| SGS collateral (D) | −0.022 (0.02) |
0.014 (0.01) |
| Collateral referenced in futures (D) | −0.020 (0.02) |
0.011 (0.04) |
| Fixed effects | day | day and borrower*lender*year |
| R squared | 0.143 | 0.537 |
| Number of observations | 14,858 | 14,596 |
|
Notes: *p < 0.1, **p < 0.05, ***p < 0.01; standard errors in parentheses clustered at the lender account level (42 clusters); state government entities and haircuts above 5 per cent in absolute value removed from regressions; D denotes a dummy variable (a) IHS refers to the inverse hyperbolic sine transformation, similar to a log transformation but capable of transforming zeros Sources: ASX; Author's calculations; RBA |
||
5.5 Intraday Timing Patterns in 2015
The algorithm data also provide detailed information on the intraday timing of interbank repo settlements. Importantly, the algorithm data contain the transactions' settlement times, which could differ from the times at which the counterparties negotiated the repos. As discussed in the previous section, some repos are likely negotiated the day before settlement.
Figure 13 illustrates the variance in repo volumes, values, spreads and maturities within an average day in the 2015 window. Some relatively low-value repos tend to occur in the early morning. A drop in volume and value occurs around 4.30 pm. Brassil et al (2016) show that unsecured lending peaks during the ‘close’ session between 4.30 pm and 5.15 pm, when banks acquire information on how the processing of SWIFT customer payments has affected their liquidity position. Given their findings, Figure 13 indicates a substitution from the repo to the unsecured market at this time, and the pick-up in repo values between 4.30 pm and 5.30 pm may reflect entities turning back to the repo market to find funds not sourced in the unsecured market.
Average spreads rise throughout the day, although the pattern is not robust after controlling for other variables such as lender and borrower characteristics. The pick-up in spreads after 6 pm is driven by a small number of repos and potentially not representative of the overall market. Average maturities decline gradually from 4.5 days around 9 am to 1 day after 6 pm. Consistent with the discussion in the previous paragraph, this could be indicative of early market activity being driven by predictable funding needs, and late activity comprising more short-term needs resulting from unexpected liquidity imbalances.
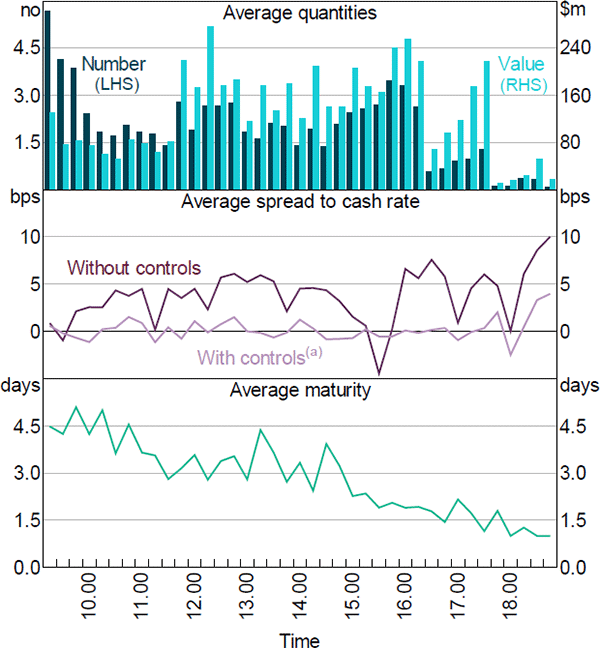
Notes:
September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions or spanning policy decisions excluded; one high turnover borrower-lender pair excluded
(a) Average of residuals from regressing spreads on maturity and dummies for day, security type (AGS, SGS and other) and borrower-lender pairs
Sources: ASX; Author's calculations; RBA
Footnotes
Section 3.3 estimates that repos with more than two transactions have a false detection rate of around 26 per cent, whereas repos with two transactions have a false detection rate of around 1 per cent. [29]
These include repos against all three collateral types, although the repos against AGS and SGS are partly hidden by the other-debt repos. [30]
Rounded interest rates have only zero decimals when measured in basis points with two decimal places. See Section 3.3.1 for further discussion. [31]
To illustrate this point, consider that a 60-day repo represents the same share of outstanding positions as 60 overnight repos of the same value. However, there are only 61 days in each data window, so we can only observe 60-day repos if they are initiated in the first day of the window. Therefore, while the share of overnight repos is calculated from many observations, the share of 60-day repos is calculated from a very small number of observations (and requires an upward adjustment to acknowledge this limited ability to observe). This 60-day share may not be representative of general activity, particularly given the possibility of false detections. It is therefore problematic to directly compare the market shares of repos that have large differences in maturities. [32]
These turnover shares are underestimates of the true values due to the issue discussed in the previous footnote. Still, the degree of underestimation depends primarily on the repo's maturity, so spikes in turnover share relative to shares at similar maturities are somewhat reliable indicators of greater activity. [33]
OMO borrowing is measured as funds received on that day from the Austraclear account that the RBA uses for OMO, also obtained from the Austraclear transactions data. The RBA typically carries out OMO at 9.20 am each morning. [34]
For this variable, Austraclear transactions with non-zero considerations that are not part of repos are interpreted as outright trades. They are only counted if they occur within two days of the first transaction of the repo. [35]
For each regression reported in this paper, repos that occur through separate transactions but are otherwise virtually identical – that is, same counterparties, settlement days, collateral type and interest rate – are aggregated into one repo to prevent estimates overweighting these repos. For the other analysis in this paper, aggregation of these repos would be less consequential. [36]
Client accounts are identified by the account name containing ‘nominee’, ‘client’, ‘custodian’ or an abbreviation of any of these. [37]
Brassil and Nodari (2018) discuss core-periphery structures in more detail with reference to the Australian unsecured interbank market. [38]
A confidence level of 90 per cent means that for every ten null hypotheses that are true, we would expect to falsely reject one of them. [39]