RDP 2018-09: Identifying Repo Market Microstructure from Securities Transactions Data 3. The Algorithm Performance
August 2018
- Download the Paper 2.7MB
In this section I assess the performance of the algorithm described in Section 2 by running it on transactions data and reporting statistics related to the detection procedure. This a) informs us about repo market practices, facilitating fine-tuning of this or other related algorithms; and b) provides an accuracy gauge of the resulting dataset of detected repos.
3.1 The Transactions Dataset
Upon request, ASX provided the RBA with securities transactions data from Austraclear, its central securities depository (CSD) for debt securities. Austraclear is the primary CSD for Australian dollar-denominated debt securities. It is linked to the Reserve Bank Information and Transfer System (RITS), the RBA's high-value settlement system. This permits Austraclear account holders to simultaneously settle securities with central bank money. In 2015, Austraclear maintained approximately 2,000 accounts held by approximately 850 entities, covering the vast majority of entities active in the Australian financial system.[15] Its records capture every debt-security movement across its users' accounts.
The dataset comprises eight two-month sample windows, covering September and October for the years 2006 to 2015, excluding 2007 and 2011.[16] Other than discount securities (i.e. securities that do not have coupon payments) issued by non-government entities and cash-only transactions, all Australian dollar-denominated debt-security transactions in these periods are included. Each transaction record contains the variables listed at the beginning of Section 2.
3.2 Running the Algorithm
Throughout the paper the algorithm is run with the following parameters (unless otherwise specified):
- Maturity cap: 14 days.
- Interest bounds: 1 percentage point around the cash rate range during the two-month data window for that year. For example, in the 2008 window, the cash rate moved from 7.25 to 6 per cent, so the interest bounds for the window are 5 and 8.25 per cent. In the 2015 window the cash rate was constant at 2 per cent, so the interest bounds for the window are 1 and 3 per cent. These bounds permit greater volatility in market rates in windows with greater volatility in the cash rate.
- Transaction cap: 6 transactions (including the focus transaction).
As mentioned in Section 2.3, all transactions involving accounts related to the RBA or ASX are removed prior to running the algorithm. In addition, as a preliminary step, detected intraday two-transaction repos are removed, if these repos satisfy C2, C3 and C5, and have an implied interest rate of zero.
Table 1 reports statistics from running the algorithm on all available data. With matrix max set at 22, the computing time for each data window ranged between 1 and 43 minutes. Around 85 to 90 per cent of detected repos have only two transactions. Almost all of the two-transaction repos are ‘unique’, meaning that neither transaction in the repo could have potentially been in another two-transaction repo (row 3). Rempel (2016) finds that in the unsecured market, unique detections have lower false detection rates than non-unique detections. Of the multiple-transaction repos, very few are detected using the iterative method, likely reflecting the low proportion of candidate vectors longer than 22 (row 6). This part of the algorithm could potentially be removed at little practical cost to speed up computing time.[17] The very low proportion of candidate vectors longer than 45 implies that computing capacity placed very few practical constraints on the results.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|---|
| Total repos (excl intraday) | 1,281 | 1,459 | 2,177 | 3,273 | 4,076 | 3,857 | 4,705 | 3,891 |
| Two transactions | 1,159 | 1,324 | 1,993 | 2,959 | 3,774 | 3,621 | 4,420 | 3,659 |
| Unique | 1,132 | 1,313 | 1,966 | 2,917 | 3,677 | 3,479 | 4,190 | 3,478 |
| More than two transactions | 122 | 135 | 184 | 314 | 302 | 236 | 285 | 232 |
| Iterative method | 0 | 0 | 1 | 5 | 14 | 0 | 9 | 0 |
| CVs with length ≤ 22 (%) | 99.2 | 82.2 | 93.7 | 91.8 | 96.5 | 98.8 | 90.1 | 99.1 |
| CVs with length ≤ 45 (%) | 100.0 | 91.2 | 99.5 | 99.6 | 99.8 | 100.0 | 97.6 | 100.0 |
| Longest CV | 28 | 89 | 50 | 54 | 54 | 30 | 83 | 36 |
| Intraday repos | 47 | 47 | 78 | 74 | 135 | 415 | 219 | 165 |
| Total transactions(a) | 20,636 | 19,873 | 27,505 | 32,743 | 38,191 | 35,565 | 41,746 | 36,911 |
| Proportion in repos (%) | 13.6 | 16.0 | 17.3 | 21.9 | 23.2 | 24.9 | 24.6 | 22.8 |
|
Notes: CV denotes candidate vectors Sources: ASX; Author's calculations |
||||||||
Table 2 reports how many and what type of transactions are in each detected repo. Very few detected repos have more than three transactions, and the sparsity of repos with six transactions indicates that the transactions cap is relatively inconsequential. Partial repayments are more common than loan increases by a small margin. Collateral movements, that is, zero-cash transactions within repos, occur rarely, and given the possibility of false detections (discussed in Section 3.3), potentially never.[18]
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|---|
| Three transactions | 104 | 107 | 137 | 206 | 203 | 179 | 202 | 182 |
| Four transactions | 16 | 20 | 35 | 71 | 66 | 45 | 50 | 35 |
| Five transactions | 1 | 6 | 8 | 19 | 26 | 5 | 19 | 11 |
| Six transactions | 1 | 2 | 4 | 18 | 7 | 7 | 14 | 4 |
| Partial repayment | 77 | 98 | 112 | 215 | 185 | 149 | 182 | 136 |
| Loan increase | 54 | 56 | 97 | 162 | 159 | 121 | 155 | 126 |
| Collateral movement | 0 | 0 | 2 | 0 | 1 | 0 | 1 | 0 |
|
Sources: ASX; Author's calculations |
||||||||
3.3 Assessing Misidentification of Repo Transactions
False detections are detected repos that are actually transactions carried out for other purposes. False omissions are actual repos whose transactions appear in the transactions data but are not detected by the algorithm. There is a trade-off between false detections and false omissions. For example, setting wider interest bounds is likely to decrease false omissions while increasing false detections. The choice of parameters and indeed the overall algorithm structure must acknowledge this trade-off and balance these two sources of error. Ashcraft and Duffie (2007), for example, only permit unsecured loans to be made at certain times of the day, and Rempel (2016) requires non-unique detected unsecured loans to have interest rates at certain increments. These choices reduce false detections but likely increase false omissions. This section demonstrates that ways to reduce the false detection rate would include narrowing the interest bounds, or bypassing the multiple-transaction repo detection stage, potentially without a large increase in false omissions.
3.3.1 Assessing false detections
The most likely cause of false detections is when groups of outright securities trades coincidentally satisfy C1 to C7. That is, a false detection can occur when two outright trades occur in opposite directions between the same counterparties, involving the same type and quantity of securities, and have considerations (i.e. cash legs) resembling principal and interest. Such considerations could be caused by a change in market price that, when annualised, is within the interest bounds. The required price increase is small. For instance, for an overnight repo when the cash rate is 7 per cent, the ‘false detection’ price increase is around 0.02 per cent. In comparison, in the 2012 to 2015 windows the median absolute daily price change for AGS and state government-issued securities (SGS) is 0.1 per cent.
False detections can be gauged by performing a placebo test on the algorithm, running it on data or algorithm parameters that are unlikely to capture any actual repos, and counting the detections. For the Canadian unsecured market, Rempel (2016) runs the Furfine algorithm on payments data after randomly reshuffling the dates so that consecutive days no longer appear consecutively in the data. Any detected overnight loans must therefore be false detections rather than actual overnight loans. However, the most likely reason for falsely detected repos – groups of outright trades that resemble repos – is dependent on the distance between transaction days. That is, small securities price changes that resemble feasible interest rates are more likely between consecutive days than between days further apart, so changing the ordering would likely underestimate false detections.[19]
Rather than using the Rempel (2016) approach, I run the algorithm on the true data with C4 set at ‘placebo’ interest bounds in which actual repos are very unlikely to occur, but that are roughly equally susceptible to falsely detecting two outright trades. For placebo bounds I use the negative of the ‘standard’ interest bounds described in Section 3.2.[20] Assuming that very small negative and positive securities price movements are equally likely, these placebo bounds and the standard bounds would have a similar number of false detections.[21] This can be interpreted as a special case of the approach by Rempel, one that uses only reshuffles that preserve distance between days. That is, a detection in the placebo bounds would appear as a repo with a positive interest rate if the loan and repayment dates were swapped. Since arbitrage relationships lead debt securities prices to move in the opposite direction to the cash rate, I focus on the 2009, 2010 and 2012 windows, in which the cash rate increased 0.25 per cent, stayed constant, and declined 0.25 per cent, respectively. The placebo bounds are also the same width as the standard bounds, so are equally susceptible to any other causes of false detections that are uniformly distributed across implied interest rates.
Table 3 reports the results from this exercise, including separate statistics for two-transaction and multiple-transaction repos.[22] Overall, the proportion of detections at placebo bounds to detections at standard bounds (the ‘false detection rate’) is 3.2 per cent. Multiple-transaction repos have a false detection rate of 26.4 per cent, contributing the majority of false detections despite being less than 10 per cent of total detected repos (at the standard bounds). This indicates that a random combination of three or more transactions is much more likely to satisfy C1 to C7 than a random combination of two transactions. For two-transaction repos alone, the overall false detection rate is 1 per cent.
| 2009 | 2010 | 2012 | Total | |
|---|---|---|---|---|
| Total repos | 1.56 | 3.76 | 3.53 | 3.16 |
| Two-transaction repos | 1.00 | 1.32 | 0.82 | 1.03 |
| Multiple-transaction repos | 7.61 | 26.75 | 37.42 | 26.38 |
|
Sources: ASX; Author's calculations |
||||
Figure 2 visualises the placebo exercise across all of the eight two-month data windows, focusing on detections within 1 percentage point from the cash rate. Consistent with false detections being randomly scattered, placebo detections are distributed roughly uniformly across the interest rate intervals, and do not appear more common at implied interest rates closer to zero (i.e. towards the right of the figure). In contrast, repo detections peak at the cash rate and quickly tail off on each side. The false detection rate would therefore almost certainly be lower if interest bounds were set more narrowly around the cash rate.
Another way to examine false detections is to look for implied interest rates that are not whole basis points. There are several feasible reasons why interest rates on actual repos may not be rounded, so the rate of non-rounded implied interest rates is best considered as an extreme upper bound on the rate of false positives. For example: interest rates could be renegotiated during the loan (and the detected repo would show a mean over the life of the repo); repos could be rolled over and interest compounded; interest rates could be agreed as fractions of a percentage point rather than as basis points; or any combination of these.
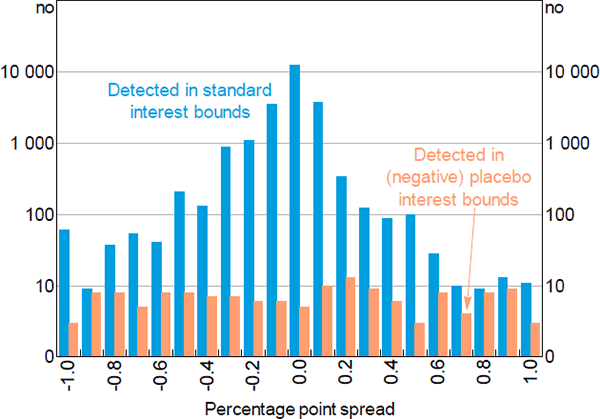
Notes: Algorithm run with 14-day maturity cap on all available transaction data; rounded to 0.1 percentage points
Sources: ASX; Author's calculations
Table 4 reports the number of repos detected with implied simple interest rates that, when measured in basis points with two decimal places, have any non-zero decimals (‘non-rounded rates’). The probability of a falsely detected random combination of transactions satisfying this criterion is around 1 per cent. Repos spanning monetary policy decisions are excluded because these are more likely to have experienced a renegotiated rate. Overall, 13 per cent of detected repos have non-rounded rates. The proportion for multiple-transaction repos is 90 per cent. While this is consistent with Table 3 showing that multiple-transaction repos having the highest false detection rates, the proportion is likely pushed up owing to the fact that repos that involve a transaction between the initial loan and final repayment are also more likely to experience renegotiated, averaged or compounded interest.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| Total repos | 14.27 | 14.61 | 14.34 | 15.49 | 13.17 | 12.59 | 10.87 | 9.29 | 12.55 |
| Two-transaction repos | 7.51 | 7.91 | 7.45 | 8.51 | 7.33 | 7.67 | 6.27 | 5.12 | 7.01 |
| Multiple-transaction repos | 81.19 | 89.52 | 91.88 | 92.27 | 93.85 | 94.76 | 88.56 | 82.81 | 90.01 |
|
Notes: Non-rounded is defined as any non-zero decimals when measured in basis points with two decimal places; repos spanning policy decisions are excluded from calculations Sources: ASX; Author's calculations |
|||||||||
3.3.2 Assessing false omissions
False omissions, defined as actual repos that appear in the transactions data but are not detected by the algorithm, can only be caused by actual repos violating conditions C1 to C9, or the constraints imposed by computing capacity. Computing constraints have been discussed in Section 3.2 and likely cause very few false omissions.
To gauge the likelihood of false omissions caused by condition violations, I count the additional repos that are detected when the conditions are relaxed in ways that accommodate the most likely reasons for their violations. The conditions and the ways I relax them are:
- C2: All transactions occur between the same two Austraclear accounts. A feasible violation would be an entity that owns multiple accounts using different accounts for the loan and repayment transactions. To test this, the Austraclear account IDs are replaced with a smaller set of IDs that group accounts held by related parties, before re-running the algorithm.[23]
- C3(i): The loan and repayment transactions involve the same ISIN. Similar in concept to the previous bullet point, ISINs can be replaced with a more general label of AGS, SGS or other.[24]
- C3(ii): All transactions involve movement of securities. Cash-only transactions could feasibly occur within repos if the interest is paid in a separate transaction to the principal repayment. Such cases would resemble a repo with zero interest, which can be detected with interest bounds at zero. Notwithstanding, repos with zero interest could also be securities loans.
- C3(iii): All transactions involve the same ISIN. In some repo markets collateral for a single repo can be spread across multiple ISINs (e.g. Fuhrer et al 2016). Market intelligence has indicated that in the Australian repo market multiple-ISIN repos occur rarely, if ever. To test this, I look for four-transaction repos involving two different AGS ISINs, with an implied net-zero FV transfer for each ISIN. Specifically, I count detections that: comprise four transactions; have two lending transactions on one day with different ISINs; and have two repayment transactions on a later day with ISINs and FVs matching the two lending transactions.[25]
To minimise the likelihood of any additional detections being false detections, the analysis is restricted to two-transaction repos (or four-transaction repos for C3(iii)). First, two-transaction repos are detected using the standard conditions and removed from the transactions data, then the algorithm is re-run with the relaxed conditions. For some of the condition relaxations, I also report the percentage of additional detections whose implied simple interest rates have two zero decimals when measured in basis points. These detections are much less likely to be false detections.
There appear to be some repos violating C2 and C3, but not many (Table 5). There is strong evidence that counterparties to a repo sometimes lend and repay using different accounts, although the frequency is 0.6 per cent of repos detected under the standard conditions. There are also repos with implied interest rates of zero. However, most of these involve accounts related to the ICSDs, which are more likely to conduct repos related to transactions occurring outside the Austraclear data. Moreover, some of these detections may be securities loans. Overall, the evidence suggests false omissions for non-ICSD-related repos are negligible.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| C2: generalised account IDs | |||||||||
| No of generalised accounts | 51 | 51 | 52 | 53 | 48 | 47 | 46 | 46 | na |
| (No of standard accounts) | (85) | (81) | (85) | (83) | (80) | (74) | (71) | (72) | na |
| Detected | 29 | 8 | 11 | 39 | 15 | 11 | 9 | 6 | 128 |
| With rounded rates (%)(a) | 84.21 | 71.43 | 70.00 | 97.30 | 92.31 | 80.00 | 71.43 | 66.67 | 85.32 |
| Relative to standard (%) | 2.50 | 0.60 | 0.55 | 1.32 | 0.40 | 0.30 | 0.20 | 0.16 | 0.56 |
| C3(i): generalised security types | |||||||||
| Detected | 14 | 7 | 5 | 20 | 17 | 22 | 33 | 29 | 147 |
| With rounded rates (%)(a) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relative to standard (%) | 1.21 | 0.53 | 0.25 | 0.68 | 0.45 | 0.61 | 0.75 | 0.79 | 0.64 |
| AGS or SGS | 1 | 4 | 3 | 10 | 6 | 12 | 4 | 4 | 44 |
| C3(ii): zero implied interest | |||||||||
| Detected | 17 | 9 | 17 | 30 | 96 | 83 | 32 | 38 | 322 |
| Relative to standard (%) | 1.47 | 0.68 | 0.85 | 1.01 | 2.54 | 2.29 | 0.72 | 1.04 | 1.41 |
| Detected excluding ICSDs | 0 | 2 | 1 | 11 | 20 | 11 | 12 | 12 | 69 |
| C3(iii): two ISINs, four transactions | |||||||||
| Detected | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
Note: (a) Detected repos spanning policy decisions removed from this calculation Sources: ASX; Author's calculations |
|||||||||
Some of the conditions C1 to C9 are not addressed in the above analysis. Violations of C4 – repos with interest rates outside the interest bounds – are feasible, but detecting these would raise the number of false detections. That is, while the number of detected repos trails off heavily away from the cash rate, the number of false detections does not (Figure 2). Gauging violations of C8 and C9 is more difficult. Most violations would have a corresponding false detection, being the other set of transactions satisfying C1 to C7 that were discarded because they overlapped the detected repo favoured by C8 and C9.[26]
Footnotes
Some statistics on Austraclear are available in CPMI (2016). [15]
The periods captured are in part determined by data availability. [16]
The code provided in the online supplementary information has an option to switch off this part of the algorithm, or to switch off multiple-transaction repo detection completely. [17]
Wakeling and Wilson (2010) report that there is no fixed convention for collateral top-ups in Australia. The transactions data are checked for signs of collateral swaps – that is, while a repo is open, a provision of a new type of collateral and a return of the original type – and no evidence for this behaviour is found. [18]
The Rempel (2016) approach has the advantage that the distribution of false detections can be estimated by repeating the exercise on many different data reshuffles. [19]
For example, if the cash rate is 4.5 per cent throughout a sample window, the standard bounds are 3.5 and 5.5 per cent, and the placebo bounds are −5.5 and −3.5 per cent. [20]
It is possible that securities lending occurs at negative interest rates. This would bias the estimated false detection rate upward. It is also possible that short-selling activity satisfies the algorithm conditions, because a short sale must typically be followed by the seller repurchasing the same securities to return to the securities lender (although the purchase may be from a different counterparty). [21]
The three years reported in Table 3 have higher false detection rates than all other years in the data. [22]
Only transactions between entities that appear in standard detected repos are retained for this exercise. [23]
This would also capture instances of the borrower replacing the collateral type during the life of the repo, if the original and replaced collateral had the same face value, and had different ISINs but the same general label. [24]
Note that these would be detected as two separate repos under the standard conditions if the considerations in the repayment transactions aligned with the two lending transactions plus interest. [25]
In an earlier version of the algorithm, the maturity was given higher priority than the number of transactions for multiple-transaction repos, and the number of repo detections was very similar. [26]