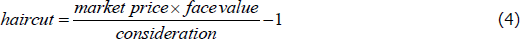Research Discussion Paper – RDP 2018-09 Identifying Repo Market Microstructure from Securities Transactions Data
1. Introduction
Short-term interbank markets are at the core of most developed financial systems. They are the first resort for financial institutions (henceforth loosely termed ‘banks’) wishing to manage the day-today liquidity needs that arise from their business-related cash flows. Moreover, the interest rates banks charge each other in these markets have flow-on effects to other interest rates throughout the economy. This pivotal role is the reason central banks use these markets for enacting monetary policy. The Reserve Bank of Australia (RBA), like many other central banks, targets the rate in the unsecured interbank market for overnight loans, termed the ‘cash rate’.
Another key component of short-term interbank markets, besides the unsecured market, is the repo market. Unsecured loans involve movements of cash only, whereas repos (i.e. secured loans) involve simultaneous movement of cash and securities. Borrowers provide and receive back securities as collateral alongside their receipt and repayment of the cash that they borrow.[1] The collateral reduces the risk to the lender – if a repo borrower defaults, the lender takes immediate ownership of the collateral, whereas if an unsecured borrower defaults, the lender joins other unsecured creditors with a claim on the borrower's assets. To minimise counterparty risk, the RBA uses repos when lending to private banks in open market operations (OMO).
Figure 1 plots available data on overnight interbank (i.e. non-RBA) loans in the Australian unsecured and repo markets. These data capture the market segments that are transacted through Australian infrastructure and exclude loans rolled over multiple nights. Although initially smaller, this repo market segment had grown to outsize the corresponding unsecured market segment by 2015.[2] Similar patterns have occurred in other regions – between 2006 and 2015, unsecured turnover in the European money market declined from €14 trillion to €3 trillion, whereas secured turnover increased from €21 trillion to €29 trillion (ECB 2015).
Notwithstanding this, there is little work studying repo market data at the level of individual loans. Loan-level data are valuable because, for example, they capture information on the borrower and lender for each transaction, potentially revealing whether position changes are supply or demand driven. They also have a daily or higher frequency, permitting identification of market reactions to shocks. The lack of loan-level analysis is likely due to data availability. Adrian et al (2014) write:
One conclusion emerging from [our work] is the need to better understand the institutional arrangements in [repo and securities lending] markets.
To that end, we find that existing data sources are incomplete. More comprehensive data collection would both deepen our understanding of the repo and [securities] lending markets and facilitate monitoring firm-level and systemic risk in these markets. (p 132)[3]
This paper provides an algorithm for extracting loan-level data on over-the-counter (OTC) repo markets from securities transactions data, which may improve the accessibility of loan-level repo data.
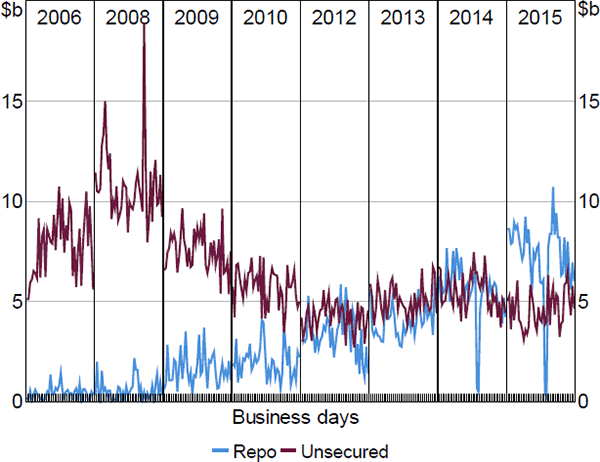
Note: Repo data from algorithm, unsecured data from daily survey of banks
Sources: ASX; Author's calculations; RBA
Loan-level data on unsecured interbank markets are commonly obtained by applying an algorithm pioneered by Furfine (1999) on US data that identifies which interbank cash transfers through central bank payments systems are interbank loans (the ‘Furfine algorithm’). The Furfine algorithm identifies pairs of payments that are consistent with a loan principal transferred in one direction, then a principal and interest repayment back the next day. Many subsequent studies have used it to analyse unsecured interbank markets at the loan level. Some notable examples are Ashcraft and Duffie (2007), analysing the intraday allocation of liquidity in the fed funds market, Afonso, Kovner and Schoar (2011), studying daily patterns in US unsecured interbank markets during the global financial crisis, and Acharya and Merrouche (2013), analysing UK unsecured interbank markets during the crisis.
Research on repo markets has tended to rely on datasets that are less detailed or of lower frequency. For example, Krishnamurthy, Nagel and Orlov (2014) study detailed data at the quarterly frequency, obtained from regulatory filings by a large proportion of US repo counterparties, and Gorton and Metrick (2012) analyse daily market-wide quotes from US dealers on interest rates and haircuts for various collateral types. Data are more readily available for market segments traded through centralised infrastructure, although these data have tended to be aggregated or anonymised before analysis. Further, OTC markets, which can be large, are omitted, limiting the conclusions that can be drawn. Copeland, Martin and Walker (2014) analyse daily data on collateral held against repos through tri-party infrastructure, collected by the Federal Reserve Bank of New York.[4] Mancini, Ranaldo and Wrampelmeyer (2016) analyse European data with several loan-level details but without counterparty information. Fuhrer, Guggenheim and Schumacher (2016) is one of the few studies that has analysed loan-level repo data, focusing on the Swiss franc repo market.
This paper describes an algorithm for extracting loan-level repo data on OTC market segments from securities transactions data, and applies the algorithm to conduct a preliminary loan-level analysis of the Australian repo market (excluding repos with the RBA). Securities transactions data are typically stored by a central securities depository (CSD) that is responsible for maintaining securities ownership records. Most CSDs permit securities transactions to involve simultaneous movement of cash and securities in opposite directions, via a link to an interbank payments system. Accordingly, OTC repos are settled through CSDs alongside other transactions such as secondary market purchases (i.e. outright trades). This is comparable to how unsecured loans are transacted through centralised payments systems alongside non-loan interbank payments. Analogous to the Furfine algorithm, the objective of the algorithm I present (the ‘repo-detection algorithm’) is to separate repo-related transactions from securities transactions occurring for other purposes.
This research is related to the small literature following Furfine (1999) that assesses and constructs modifications of the Furfine algorithm (‘Furfine-type algorithms’). Armantier and Copeland (2012) and Kovner and Skeie (2013) compare data from the Furfine algorithm with internal data from two banks and with regulatory data, respectively. Kuo et al (2013) generalise the Furfine algorithm to detect term loans rather than overnight loans. Arciero et al (2016) calibrate, run and assess the algorithm using European payments data. Rempel (2016) estimates the Furfine algorithm's rates of false detections, proposing some modifications to improve performance. Brassil, Hughson and McManus (2016) appear to be the first to detect loans that comprise more than two transactions (‘multiple-transaction loans’), finding their augmentation to noticeably improve detections in the Australian unsecured market.
Like Furfine-type algorithms, the repo-detection algorithm identifies groups of cash movements that resemble a loan followed by a repayment with interest. However, Furfine-type algorithms rely on the market convention that unsecured loan principals are multiples of, for example, $100,000, which is not followed in the Australian repo market. On the other hand, securities transactions data contain more information than payments data – most notably the type and quantity of securities transferred. By requiring that the securities initially provided as collateral are the same type and quantity as those returned, the repo-detection algorithm essentially removes the need to require that loan principals are round numbers. In addition, it detects multiple-transaction repos, like Brassil et al (2016), although the difference in market conventions across repo and unsecured markets necessitates a different approach.
The repo-detection algorithm is described in more detail in Section 2. It is represented as a set of conditions that identify a group of securities transactions as a detected repo. I then describe the procedure for applying these conditions to the data. To detect multiple-transaction repos, I appropriately adapt the subset sums problem (a well-known exercise in computer science) to the requirement that all collateral provided in a repo is subsequently returned. The R code for the algorithm, with detailed comments, is available in the online supplementary information.
In Section 3, I run the algorithm on securities transactions data from Austraclear that cover several two-month windows of transactions from 2006 to 2015, and assess its performance. Multiple-transaction repos are common but occur with much lower frequency than two-transaction repos. Using placebo tests that can be interpreted as a special case of the approach of Rempel (2016), I estimate around 3 per cent of the algorithm detections to be false detections, although excluding multiple-transaction repos reduces this to around 1 per cent. To gauge the incidence of repos missed by the algorithm (but present in the transactions data), that is, false omissions, I relax some of the conditions assumed in Section 2 and find that very few additional repos are detected.
Readers more interested in the Australian repo market data than the algorithm itself can skip to Sections 4 and 5. Section 4 provides context for the analysis in Section 5 by comparing the algorithm data with aggregated repo data from the Australian Prudential Regulation Authority (APRA). The APRA data imply substantially larger repo positions. There are, however, reasons to expect differences. For example, some repo positions reported to APRA are likely transacted through international CSDs (ICSDs) located in Europe with offshore counterparties. Observations in the algorithm data and APRA data have a robust positive relationship with correlations of around 0.5.
Section 5 provides a preliminary description of the Australian short-term repo market, that is, of 14-day maturity or less, as informed by the algorithm data obtained in Section 3. In the 2015 window, the average total value of repos open each night is around $12 billion, compared to around $5 billion in 2006.[5] The majority of repos are collateralised by Australian Government securities (AGS), although there is little market concentration in particular AGS. In 2006 repos open for one week had the largest market share, although by 2015 the market had largely shifted to overnight maturities. Repo rates display substantial cross-sectional variation across an interval of around 50 basis points, and drift upward between 2006 and 2015. For maturities up to 14 days, rates are not strongly related to maturity. Larger loans have higher rates.
In the two-month 2015 window, around half of the repo turnover in the market segment captured is between one foreign lender and one Australian borrower. Otherwise, most of the turnover is distributed across around 20 Australian and foreign banks and a few Austraclear accounts related to banks' clients. Repo counterparties tend to be either highly integrated within the market, dealing with around ten counterparties, or active only in the periphery, dealing only with one or two banks from the highly integrated segment. Repo haircuts are scattered around zero, not following any obvious patterns. On average, repo settlement activity subsides late in the day when unsecured market activity peaks. Longer maturity repos tend to be initiated earlier in the day than shorter maturity repos.
2. The Repo-detection Algorithm
The algorithm detects groups of securities transactions that appear to comprise a repo, that is, that satisfy a set of characteristics that repos are assumed to have. Transactions not in these groups are assumed to occur for other reasons. The following information about each transaction is required:
- Settlement time: the day and time the transaction took place.[6]
- Counterparties: CSD account IDs for the securities sender and the securities receiver.
- International securities identification number (ISIN): the type of securities transferred.
- Face value (FV): the face value of securities transferred.
- Consideration: the amount of money, if any, transferred in the opposite direction to the securities.
The key idea is similar to that of the Furfine algorithm, which identifies pairs of payments that are consistent with a loan principal transferred in one direction, then a principal and interest repayment transferred together in the opposite direction the next day. Furfine-type algorithms rely on the unsecured market convention that loans are made in multiples of, for example, $100,000. This convention is not, however, followed in the Australian repo market. Nonetheless, by utilising a larger set of information, that is, including ISINs and FVs, a repo-detection algorithm can still effectively identify repo transactions. Relative to Furfine-type algorithms, the difference in market conventions implies that the repo-detection algorithm must treat more transactions as potential loan initiations, but the ISIN and FV information reduces the number of subsequent transactions that potentially form a repo with any loan-initiation transaction. The net effect is that the computational load remains feasible.
The repo-detection algorithm also detects loans comprising more than two transactions, in contrast to most Furfine-type algorithms that only search for payment pairs. Multiple transaction loans occur if the lender increases the loan size before it is repaid, or the borrower repays the loan in multiple instalments, or there is a collateral top-up or drawdown, or any combination of these happens. Such loans would be missed by an algorithm detecting only transaction pairs. Brassil et al (2016) show that these multiple-transaction loans occur frequently in the unsecured market. In Section 3.2, I show that multiple-transaction repos also occur, but are less common than two-transaction repos.
2.1 Underlying Assumptions
The repo-detection algorithm can be characterised as a collection of conditions that maps a set of securities transactions into a set of ‘detected repos’. The conditions have three parameters: maturity cap, determining the maximum maturity of detected repos, measured in whole days; interest bounds, determining the minimum and maximum annualised simple interest rates that detected repos can have; and transaction cap, determining the maximum number of transactions that can comprise a detected repo.
The conditions that together define a set of transactions as a ‘detected repo’ are:
C1. All transactions occur within an interval of days not greater than maturity cap.
C2. All transactions take place between the same two CSD accounts.
C3. All transactions involve movement of securities with the same ISIN.
C4. The implied simple interest rate from all cash movements in the set is in the interest bounds.
C5. The set involves a net-zero transfer of securities; that is, the FV of securities provided as collateral equals the FV returned.
C6. At no point does the lender return more securities than it has received.
C7. The number of transactions in the set is not more than the transaction cap.
C8. If there exist overlapping sets satisfying C1 to C7, sets with fewer transactions are retained over other sets they overlap with.
C9. If C8 does not remove all overlapping sets (i.e. overlapping sets have equally few transactions), remaining overlaps are in some cases removed by favouring sets with the shortest implied maturity, or by otherwise choosing arbitrarily.[7]
C1 to C5 capture the key assumed characteristics of a short-term repo – opposing transactions between the same accounts within a short period of time, with cash and securities movements consistent with a loan and its collateral. C6 and C7 impose realistic bounds on detected repos that serve to reduce false detections and the required computing capacity.
C8 and C9 handle situations in which a transaction appears in multiple sets that each appear to be a repo. Sets with characteristics that repos tend to satisfy are favoured. Fewer-transaction sets are favoured first, and, in some cases, sets with shorter implied maturities are favoured next. If there still remain overlapping sets, for example, with equally few transactions and equally short maturities, a set is selected arbitrarily, given that the remaining sets are close enough to have little consequence for the dataset of detected repos.
2.2 How the Algorithm Works and the Subset Sums Problem
The process for detecting a two-transaction repo involves first selecting a ‘focus transaction’ – a transaction to treat as a potential loan initiation – then checking whether any subsequent transaction in the dataset pairwise satisfies C1 to C5 with the focus transaction. In contrast, for multiple-transaction repos, C4 and C5 do not permit subsequent transactions to be checked individually; each possible combination of subsequent transactions must be checked as a set. This heavily increases the required computing capacity – a single focus transaction with, for example, 20 potential subsequent transactions, gives over a million possible combinations.[8] Accordingly, it is important to comprehensively narrow down the number of potential transactions before applying C4 and C5, and then to apply C4 and C5 using an efficient method. The relative efficiency of different methods is in part determined by the programming language used – the algorithm presented here is written in R.
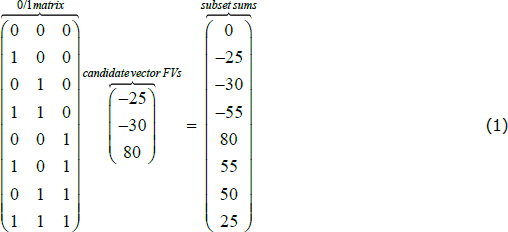
For multiple-transaction repos, a focus transaction is selected, then a ‘candidate vector’ is formed of all other transactions that satisfy C1, C2 and C3. The candidate vector is then trimmed by applying C6. Next, all subsets of the candidate vector are checked against C5. Detecting subsets with zero net FV movement is a case of the ‘subset sums problem’, familiar to computer scientists. I combine two methods to solve the problem, implemented in R: first, a matrix-algebra method that checks subsets of limited size (bound above by computing capacity), then, if unsuccessful, an iterative method that checks larger subsets. The relative speed of each method can depend on computer specifications.[9] The user decides the workload allocated to each method by specifying a ‘matrix max’ parameter, which determines the maximum subset size to check with the matrix-algebra method.[10] Subsets satisfying C5 are then screened against C4, C6 and C7, and overlaps removed by applying C8 and C9.
The matrix-algebra method is illustrated in Equation (1). First, elements of the candidate vector of FVs are made negative if the transactions are in the same direction to the focus transaction. Then this vector of FVs is pre-multiplied by a matrix of 0s and 1s that represents all possible subsets, and the result is a vector of subset sums that can be checked for values equalling the focus transaction FV. The 0/1 matrix has a column for each transaction in the candidate vector, and a row for every possible subset, with 1s where the corresponding candidate element is present in that subset. In Equation (1), if the focus transaction FV is 50 and the candidate vector FVs are (−25, −30, 80), the subset represented by the (0, 1, 1) row of the 0/1 matrix is a candidate subset, because the corresponding element of the subset sums vector equals 50.
The 0/1 matrix can be quickly generated using the base R ‘expand.grid’ function, although its size exceeds memory limits for long candidate vectors. For the applications in this paper and the computing resources available, the maximum achievable length is 22. Matrix max can be set no higher than this maximum. For candidate vectors longer than matrix max, the vector is trimmed to matrix max length by excluding transactions furthest in time from the focus transaction, and then checked using the matrix-algebra method.
If a repo is not detected by the matrix-algebra method I then use an approach that can accommodate longer candidate vectors. The full candidate vector is trimmed to a longer threshold, determined by computing capacity (45 in this paper), prioritising transactions closest in time to the focus transaction. This vector is then checked using an ‘iterative’ method. Denoting the transaction cap in C7 as K, the method iterates through k = 1, …, K − 1, using the base R ‘combn’ function to construct each possible combination of k candidate vector elements, and checking their FV sums. For each k, this method is similar to applying the matrix-algebra method on the subset of the 0/1 matrix that contains only rows with k non-zero elements. For example, for k = 1 these are the rows that form the identity matrix. If there are candidate vectors longer than this higher threshold, the computing constraints result in unchecked potential combinations. Section 3.2 assesses the consequences of this.
2.3 The Algorithm Procedure
Before running the algorithm, any transactions involving the RBA or ASX are removed. Detected intraday repos, defined as two transactions on the same day with the same ISIN, FV and consideration, and in opposite directions between the same two accounts, are also removed. This assumes an intraday interest rate of zero, consistent with intraday repos on offer from the RBA, although other assumptions on intraday interest rates or fees can easily be imposed.[11]
For two-transaction repos, the process is essentially:
Step 1.1 Select a transaction as the ‘focus transaction’.
1.2 Find all other transactions that satisfy C1 to C5 pairwise with the focus transaction (if any). Store the pairs.[12]
1.3 Repeat 1.1 and 1.2, treating every transaction in the dataset as a focus transaction. Store all pairs.
1.4 Sort all the stored pairs by increasing maturity, measured in days, with equal maturities ordered arbitrarily.
1.5 Define the first pair in the sorted list as a detected repo, remove from the list any subsequent pairs that it overlaps, and repeat down to the bottom of the list of pairs.
Transactions in detected two-transaction repos are then removed and the remaining transactions are checked for multiple-transaction repos. The process is essentially:
Step 2.1 Select a transaction as the ‘focus transaction’.
2.2 Find all other transactions that satisfy C1 to C3 pairwise with the focus transaction. Store these together in a ‘candidate vector’ that is linked to the focus transaction.
2.3 Remove transactions from the candidate vector that would violate C6 in any combination.
2.4 Repeat 2.1 to 2.3, treating all transactions as a focus transaction, and collect all candidate vectors.
2.5 Define a temporary maximum number of transactions, starting with three.
2.6 Select a candidate vector. Remove any transactions in already-defined detected repos.
2.7 Find subsets of the candidate vector with FVs summing to the focus-transaction FV using the methods discussed in Section 2.2, after making the FVs of transactions in the same direction as the focus transaction negative. Remove subsets not satisfying C4 or exceeding the temporary maximum number of transactions. If multiple remain, keep only the minimum-maturity subsets (measured as nights between first and last transaction), and if multiple still remain, arbitrarily select one. Define it as a detected repo.[13]
2.8 Repeat 2.6 and 2.7, working through every candidate vector.
2.9 Increase the maximum transaction number specified in 0 by one, repeat 2.6 to 2.8, and then repeat until the transaction cap is reached.[14]
The online supplementary information contains the R code with explanations included as comments.
3. The Algorithm Performance
In this section I assess the performance of the algorithm described in Section 2 by running it on transactions data and reporting statistics related to the detection procedure. This a) informs us about repo market practices, facilitating fine-tuning of this or other related algorithms; and b) provides an accuracy gauge of the resulting dataset of detected repos.
3.1 The Transactions Dataset
Upon request, ASX provided the RBA with securities transactions data from Austraclear, its central securities depository (CSD) for debt securities. Austraclear is the primary CSD for Australian dollar-denominated debt securities. It is linked to the Reserve Bank Information and Transfer System (RITS), the RBA's high-value settlement system. This permits Austraclear account holders to simultaneously settle securities with central bank money. In 2015, Austraclear maintained approximately 2,000 accounts held by approximately 850 entities, covering the vast majority of entities active in the Australian financial system.[15] Its records capture every debt-security movement across its users' accounts.
The dataset comprises eight two-month sample windows, covering September and October for the years 2006 to 2015, excluding 2007 and 2011.[16] Other than discount securities (i.e. securities that do not have coupon payments) issued by non-government entities and cash-only transactions, all Australian dollar-denominated debt-security transactions in these periods are included. Each transaction record contains the variables listed at the beginning of Section 2.
3.2 Running the Algorithm
Throughout the paper the algorithm is run with the following parameters (unless otherwise specified):
- Maturity cap: 14 days.
- Interest bounds: 1 percentage point around the cash rate range during the two-month data window for that year. For example, in the 2008 window, the cash rate moved from 7.25 to 6 per cent, so the interest bounds for the window are 5 and 8.25 per cent. In the 2015 window the cash rate was constant at 2 per cent, so the interest bounds for the window are 1 and 3 per cent. These bounds permit greater volatility in market rates in windows with greater volatility in the cash rate.
- Transaction cap: 6 transactions (including the focus transaction).
As mentioned in Section 2.3, all transactions involving accounts related to the RBA or ASX are removed prior to running the algorithm. In addition, as a preliminary step, detected intraday two-transaction repos are removed, if these repos satisfy C2, C3 and C5, and have an implied interest rate of zero.
Table 1 reports statistics from running the algorithm on all available data. With matrix max set at 22, the computing time for each data window ranged between 1 and 43 minutes. Around 85 to 90 per cent of detected repos have only two transactions. Almost all of the two-transaction repos are ‘unique’, meaning that neither transaction in the repo could have potentially been in another two-transaction repo (row 3). Rempel (2016) finds that in the unsecured market, unique detections have lower false detection rates than non-unique detections. Of the multiple-transaction repos, very few are detected using the iterative method, likely reflecting the low proportion of candidate vectors longer than 22 (row 6). This part of the algorithm could potentially be removed at little practical cost to speed up computing time.[17] The very low proportion of candidate vectors longer than 45 implies that computing capacity placed very few practical constraints on the results.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|---|
| Total repos (excl intraday) | 1,281 | 1,459 | 2,177 | 3,273 | 4,076 | 3,857 | 4,705 | 3,891 |
| Two transactions | 1,159 | 1,324 | 1,993 | 2,959 | 3,774 | 3,621 | 4,420 | 3,659 |
| Unique | 1,132 | 1,313 | 1,966 | 2,917 | 3,677 | 3,479 | 4,190 | 3,478 |
| More than two transactions | 122 | 135 | 184 | 314 | 302 | 236 | 285 | 232 |
| Iterative method | 0 | 0 | 1 | 5 | 14 | 0 | 9 | 0 |
| CVs with length ≤ 22 (%) | 99.2 | 82.2 | 93.7 | 91.8 | 96.5 | 98.8 | 90.1 | 99.1 |
| CVs with length ≤ 45 (%) | 100.0 | 91.2 | 99.5 | 99.6 | 99.8 | 100.0 | 97.6 | 100.0 |
| Longest CV | 28 | 89 | 50 | 54 | 54 | 30 | 83 | 36 |
| Intraday repos | 47 | 47 | 78 | 74 | 135 | 415 | 219 | 165 |
| Total transactions(a) | 20,636 | 19,873 | 27,505 | 32,743 | 38,191 | 35,565 | 41,746 | 36,911 |
| Proportion in repos (%) | 13.6 | 16.0 | 17.3 | 21.9 | 23.2 | 24.9 | 24.6 | 22.8 |
|
Notes: CV denotes candidate vectors Sources: ASX; Author's calculations |
||||||||
Table 2 reports how many and what type of transactions are in each detected repo. Very few detected repos have more than three transactions, and the sparsity of repos with six transactions indicates that the transactions cap is relatively inconsequential. Partial repayments are more common than loan increases by a small margin. Collateral movements, that is, zero-cash transactions within repos, occur rarely, and given the possibility of false detections (discussed in Section 3.3), potentially never.[18]
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|---|
| Three transactions | 104 | 107 | 137 | 206 | 203 | 179 | 202 | 182 |
| Four transactions | 16 | 20 | 35 | 71 | 66 | 45 | 50 | 35 |
| Five transactions | 1 | 6 | 8 | 19 | 26 | 5 | 19 | 11 |
| Six transactions | 1 | 2 | 4 | 18 | 7 | 7 | 14 | 4 |
| Partial repayment | 77 | 98 | 112 | 215 | 185 | 149 | 182 | 136 |
| Loan increase | 54 | 56 | 97 | 162 | 159 | 121 | 155 | 126 |
| Collateral movement | 0 | 0 | 2 | 0 | 1 | 0 | 1 | 0 |
|
Sources: ASX; Author's calculations |
||||||||
3.3 Assessing Misidentification of Repo Transactions
False detections are detected repos that are actually transactions carried out for other purposes. False omissions are actual repos whose transactions appear in the transactions data but are not detected by the algorithm. There is a trade-off between false detections and false omissions. For example, setting wider interest bounds is likely to decrease false omissions while increasing false detections. The choice of parameters and indeed the overall algorithm structure must acknowledge this trade-off and balance these two sources of error. Ashcraft and Duffie (2007), for example, only permit unsecured loans to be made at certain times of the day, and Rempel (2016) requires non-unique detected unsecured loans to have interest rates at certain increments. These choices reduce false detections but likely increase false omissions. This section demonstrates that ways to reduce the false detection rate would include narrowing the interest bounds, or bypassing the multiple-transaction repo detection stage, potentially without a large increase in false omissions.
3.3.1 Assessing false detections
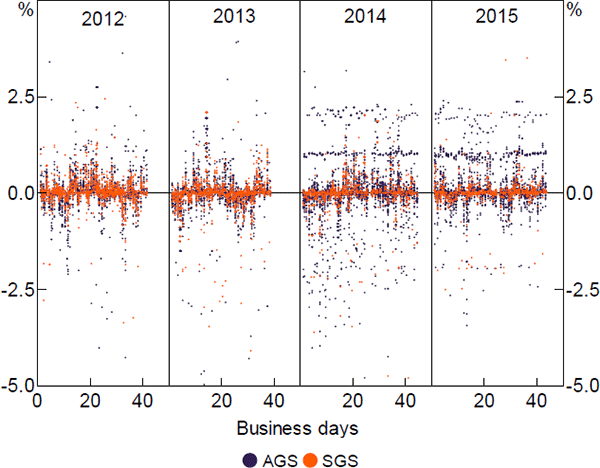
The most likely cause of false detections is when groups of outright securities trades coincidentally satisfy C1 to C7. That is, a false detection can occur when two outright trades occur in opposite directions between the same counterparties, involving the same type and quantity of securities, and have considerations (i.e. cash legs) resembling principal and interest. Such considerations could be caused by a change in market price that, when annualised, is within the interest bounds. The required price increase is small. For instance, for an overnight repo when the cash rate is 7 per cent, the ‘false detection’ price increase is around 0.02 per cent. In comparison, in the 2012 to 2015 windows the median absolute daily price change for AGS and state government-issued securities (SGS) is 0.1 per cent.
False detections can be gauged by performing a placebo test on the algorithm, running it on data or algorithm parameters that are unlikely to capture any actual repos, and counting the detections. For the Canadian unsecured market, Rempel (2016) runs the Furfine algorithm on payments data after randomly reshuffling the dates so that consecutive days no longer appear consecutively in the data. Any detected overnight loans must therefore be false detections rather than actual overnight loans. However, the most likely reason for falsely detected repos – groups of outright trades that resemble repos – is dependent on the distance between transaction days. That is, small securities price changes that resemble feasible interest rates are more likely between consecutive days than between days further apart, so changing the ordering would likely underestimate false detections.[19]
Rather than using the Rempel (2016) approach, I run the algorithm on the true data with C4 set at ‘placebo’ interest bounds in which actual repos are very unlikely to occur, but that are roughly equally susceptible to falsely detecting two outright trades. For placebo bounds I use the negative of the ‘standard’ interest bounds described in Section 3.2.[20] Assuming that very small negative and positive securities price movements are equally likely, these placebo bounds and the standard bounds would have a similar number of false detections.[21] This can be interpreted as a special case of the approach by Rempel, one that uses only reshuffles that preserve distance between days. That is, a detection in the placebo bounds would appear as a repo with a positive interest rate if the loan and repayment dates were swapped. Since arbitrage relationships lead debt securities prices to move in the opposite direction to the cash rate, I focus on the 2009, 2010 and 2012 windows, in which the cash rate increased 0.25 per cent, stayed constant, and declined 0.25 per cent, respectively. The placebo bounds are also the same width as the standard bounds, so are equally susceptible to any other causes of false detections that are uniformly distributed across implied interest rates.
Table 3 reports the results from this exercise, including separate statistics for two-transaction and multiple-transaction repos.[22] Overall, the proportion of detections at placebo bounds to detections at standard bounds (the ‘false detection rate’) is 3.2 per cent. Multiple-transaction repos have a false detection rate of 26.4 per cent, contributing the majority of false detections despite being less than 10 per cent of total detected repos (at the standard bounds). This indicates that a random combination of three or more transactions is much more likely to satisfy C1 to C7 than a random combination of two transactions. For two-transaction repos alone, the overall false detection rate is 1 per cent.
| 2009 | 2010 | 2012 | Total | |
|---|---|---|---|---|
| Total repos | 1.56 | 3.76 | 3.53 | 3.16 |
| Two-transaction repos | 1.00 | 1.32 | 0.82 | 1.03 |
| Multiple-transaction repos | 7.61 | 26.75 | 37.42 | 26.38 |
|
Sources: ASX; Author's calculations |
||||
Figure 2 visualises the placebo exercise across all of the eight two-month data windows, focusing on detections within 1 percentage point from the cash rate. Consistent with false detections being randomly scattered, placebo detections are distributed roughly uniformly across the interest rate intervals, and do not appear more common at implied interest rates closer to zero (i.e. towards the right of the figure). In contrast, repo detections peak at the cash rate and quickly tail off on each side. The false detection rate would therefore almost certainly be lower if interest bounds were set more narrowly around the cash rate.
Another way to examine false detections is to look for implied interest rates that are not whole basis points. There are several feasible reasons why interest rates on actual repos may not be rounded, so the rate of non-rounded implied interest rates is best considered as an extreme upper bound on the rate of false positives. For example: interest rates could be renegotiated during the loan (and the detected repo would show a mean over the life of the repo); repos could be rolled over and interest compounded; interest rates could be agreed as fractions of a percentage point rather than as basis points; or any combination of these.
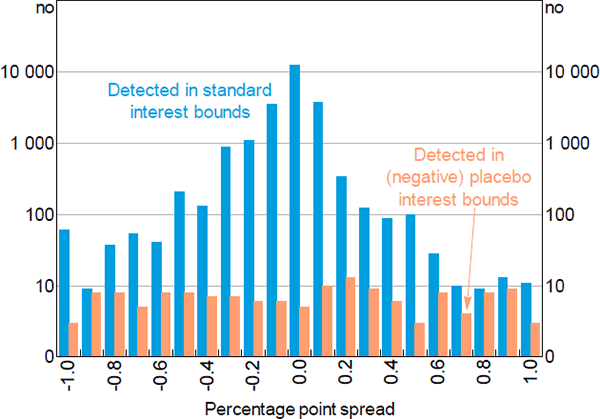
Notes: Algorithm run with 14-day maturity cap on all available transaction data; rounded to 0.1 percentage points
Sources: ASX; Author's calculations
Table 4 reports the number of repos detected with implied simple interest rates that, when measured in basis points with two decimal places, have any non-zero decimals (‘non-rounded rates’). The probability of a falsely detected random combination of transactions satisfying this criterion is around 1 per cent. Repos spanning monetary policy decisions are excluded because these are more likely to have experienced a renegotiated rate. Overall, 13 per cent of detected repos have non-rounded rates. The proportion for multiple-transaction repos is 90 per cent. While this is consistent with Table 3 showing that multiple-transaction repos having the highest false detection rates, the proportion is likely pushed up owing to the fact that repos that involve a transaction between the initial loan and final repayment are also more likely to experience renegotiated, averaged or compounded interest.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| Total repos | 14.27 | 14.61 | 14.34 | 15.49 | 13.17 | 12.59 | 10.87 | 9.29 | 12.55 |
| Two-transaction repos | 7.51 | 7.91 | 7.45 | 8.51 | 7.33 | 7.67 | 6.27 | 5.12 | 7.01 |
| Multiple-transaction repos | 81.19 | 89.52 | 91.88 | 92.27 | 93.85 | 94.76 | 88.56 | 82.81 | 90.01 |
|
Notes: Non-rounded is defined as any non-zero decimals when measured in basis points with two decimal places; repos spanning policy decisions are excluded from calculations Sources: ASX; Author's calculations |
|||||||||
3.3.2 Assessing false omissions
False omissions, defined as actual repos that appear in the transactions data but are not detected by the algorithm, can only be caused by actual repos violating conditions C1 to C9, or the constraints imposed by computing capacity. Computing constraints have been discussed in Section 3.2 and likely cause very few false omissions.
To gauge the likelihood of false omissions caused by condition violations, I count the additional repos that are detected when the conditions are relaxed in ways that accommodate the most likely reasons for their violations. The conditions and the ways I relax them are:
- C2: All transactions occur between the same two Austraclear accounts. A feasible violation would be an entity that owns multiple accounts using different accounts for the loan and repayment transactions. To test this, the Austraclear account IDs are replaced with a smaller set of IDs that group accounts held by related parties, before re-running the algorithm.[23]
- C3(i): The loan and repayment transactions involve the same ISIN. Similar in concept to the previous bullet point, ISINs can be replaced with a more general label of AGS, SGS or other.[24]
- C3(ii): All transactions involve movement of securities. Cash-only transactions could feasibly occur within repos if the interest is paid in a separate transaction to the principal repayment. Such cases would resemble a repo with zero interest, which can be detected with interest bounds at zero. Notwithstanding, repos with zero interest could also be securities loans.
- C3(iii): All transactions involve the same ISIN. In some repo markets collateral for a single repo can be spread across multiple ISINs (e.g. Fuhrer et al 2016). Market intelligence has indicated that in the Australian repo market multiple-ISIN repos occur rarely, if ever. To test this, I look for four-transaction repos involving two different AGS ISINs, with an implied net-zero FV transfer for each ISIN. Specifically, I count detections that: comprise four transactions; have two lending transactions on one day with different ISINs; and have two repayment transactions on a later day with ISINs and FVs matching the two lending transactions.[25]
To minimise the likelihood of any additional detections being false detections, the analysis is restricted to two-transaction repos (or four-transaction repos for C3(iii)). First, two-transaction repos are detected using the standard conditions and removed from the transactions data, then the algorithm is re-run with the relaxed conditions. For some of the condition relaxations, I also report the percentage of additional detections whose implied simple interest rates have two zero decimals when measured in basis points. These detections are much less likely to be false detections.
There appear to be some repos violating C2 and C3, but not many (Table 5). There is strong evidence that counterparties to a repo sometimes lend and repay using different accounts, although the frequency is 0.6 per cent of repos detected under the standard conditions. There are also repos with implied interest rates of zero. However, most of these involve accounts related to the ICSDs, which are more likely to conduct repos related to transactions occurring outside the Austraclear data. Moreover, some of these detections may be securities loans. Overall, the evidence suggests false omissions for non-ICSD-related repos are negligible.
| 2006 | 2008 | 2009 | 2010 | 2012 | 2013 | 2014 | 2015 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| C2: generalised account IDs | |||||||||
| No of generalised accounts | 51 | 51 | 52 | 53 | 48 | 47 | 46 | 46 | na |
| (No of standard accounts) | (85) | (81) | (85) | (83) | (80) | (74) | (71) | (72) | na |
| Detected | 29 | 8 | 11 | 39 | 15 | 11 | 9 | 6 | 128 |
| With rounded rates (%)(a) | 84.21 | 71.43 | 70.00 | 97.30 | 92.31 | 80.00 | 71.43 | 66.67 | 85.32 |
| Relative to standard (%) | 2.50 | 0.60 | 0.55 | 1.32 | 0.40 | 0.30 | 0.20 | 0.16 | 0.56 |
| C3(i): generalised security types | |||||||||
| Detected | 14 | 7 | 5 | 20 | 17 | 22 | 33 | 29 | 147 |
| With rounded rates (%)(a) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relative to standard (%) | 1.21 | 0.53 | 0.25 | 0.68 | 0.45 | 0.61 | 0.75 | 0.79 | 0.64 |
| AGS or SGS | 1 | 4 | 3 | 10 | 6 | 12 | 4 | 4 | 44 |
| C3(ii): zero implied interest | |||||||||
| Detected | 17 | 9 | 17 | 30 | 96 | 83 | 32 | 38 | 322 |
| Relative to standard (%) | 1.47 | 0.68 | 0.85 | 1.01 | 2.54 | 2.29 | 0.72 | 1.04 | 1.41 |
| Detected excluding ICSDs | 0 | 2 | 1 | 11 | 20 | 11 | 12 | 12 | 69 |
| C3(iii): two ISINs, four transactions | |||||||||
| Detected | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
Note: (a) Detected repos spanning policy decisions removed from this calculation Sources: ASX; Author's calculations |
|||||||||
Some of the conditions C1 to C9 are not addressed in the above analysis. Violations of C4 – repos with interest rates outside the interest bounds – are feasible, but detecting these would raise the number of false detections. That is, while the number of detected repos trails off heavily away from the cash rate, the number of false detections does not (Figure 2). Gauging violations of C8 and C9 is more difficult. Most violations would have a corresponding false detection, being the other set of transactions satisfying C1 to C7 that were discarded because they overlapped the detected repo favoured by C8 and C9.[26]
4. Comparing the Output with Prudential Data
The RBA analyses partially aggregated data on repo positions collected by the Australian Prudential Regulation Authority (APRA).[27] Registered financial corporations (RFCs) with assets above $500 million and Australian-licensed authorised deposit-taking institutions (ADIs) provide quarterly reports of repo and securities-lending positions held on their domestic books. They report the value of aggregate positions per counterparty type per collateral type, separately for borrowing and lending positions. There are twelve counterparty types, one being the RBA, and four collateral types, comprising AGS, SGS, other debt and equities. For example, 1 of the 96 figures in each entity's quarterly report is lending positions to non-resident counterparties against AGS collateral.
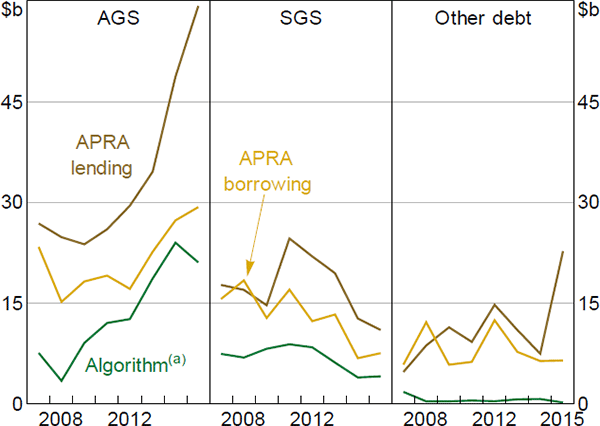
The APRA data generate two aggregated series – repo lending by reporting entities and repo borrowing by reporting entities (excluding from the RBA). The difference between these reflects net lending from reporting entities to non-reporting entities such as foreign institutions. The algorithm data can be compared to these series by aggregating detected repos that are open at September ends (Figure 3).[28] These algorithm and APRA series display broadly similar trends for AGS and SGS repos. However, the algorithm positions are smaller than the quantities reported to APRA, more so for the APRA lending series. There are several likely reasons. For repos against ‘other debt’, the difference would include any repos against discount securities, which are not in the transactions dataset I analyse and therefore not detected by the algorithm.
Notes:
Austraclear sample years are 2006, 2008, 2009, 2010, 2012, 2013, 2014 and 2015
(a) Algorithm run with 61-day maturity cap
Sources: APRA; ASX; Author's calculations; RBA
For AGS and SGS collateral, the difference likely reflects repos transacted through infrastructure other than Austraclear. Two ICSDs – Euroclear and Clearstream – enable their participants to transact Australian dollar-denominated securities that are ultimately held in Austraclear, but without transactions between Austraclear accounts taking place. The securities are held by a nominee with an Austraclear account on behalf of the ICSD, and the ICSD holds them on behalf of its participants. When the ICSD participants transact with each other the ICSD changes its own records of the securities' ownership but, in Austraclear, the securities remain in the nominee's account. Since the ICSDs have no direct link to RITS, any Australian-dollar cash settled simultaneously with these transactions takes place across accounts at a private bank employed by the ICSD.
This reason for the difference across data sources – the APRA data capturing repos settled through foreign infrastructure – is consistent with the algorithm figures being closer to the APRA borrowing figures than the APRA lending figures (Figure 3). Recall that the gap between the APRA lending and borrowing series reflects net lending from entities that report to APRA to entities that do not. Becker and Rickards (2017) attribute a substantial part of this net lending to demand from non-residents for Australian dollar repo funding as part of international arbitrage positions. Since non-residents are more likely to hold ICSD accounts than Austraclear accounts, it seems likely that these lending positions would not appear in the algorithm data.
There are several more reasons why repos could be reported to APRA but not appear in the algorithm data. First, like repos through ICSDs, other repos could occur within a single Austraclear account (thus, without any Austraclear transactions), if they are between counterparties that are part of the same company, between two clients of the same Austraclear participant, or between an Austraclear participant and one of its clients. Second, repos would be absent from these algorithm data if any of their transactions occur before or after the two-month transaction sample ends. This is likely for repos open longer than a month and definite for repos open longer than two months. Third, repos involving Australian dollar-denominated securities but foreign currency would not be detected because the cash side would not appear in the Austraclear data. Fourth, securities loans are reported to APRA but, if the interest rate is below the interest bounds, they would not be detected by the algorithm. This is plausible given what is known about securities lending markets. Finally, repos initiated on the same day between the same counterparties and involving the same ISIN can be bilaterally netted before being transacted in Austraclear, but the gross positions may still be reported to APRA. It is also possible that repos reported to APRA are netted against trades in the underlying securities before being transacted in Austraclear.
To more formally compare the datasets, I regress APRA observations on corresponding algorithm observations, similar to the approach by Kovner and Skeie (2013). Three levels of data aggregation are considered: an observation per entity per year per collateral type; an observation per entity per collateral type (i.e. aggregated across years); and an observation per year per collateral type (i.e. aggregated across entities). To better align the datasets, entities whose APRA-data and Austraclear-account IDs cannot be closely matched are removed. The algorithm is run with a maturity cap of 61 days, and the APRA observations exclude positions held with counterparties other than banks, RFCs, other ADIs and non-residents.
Table 6 reports the estimates. Regression exogeneity assumptions could feasibly be violated, so the estimates and significance levels should be interpreted with some caution. Notwithstanding this, in all specifications the estimated slope coefficients indicate a statistically significant positive relationship between the algorithm and APRA data, denoted by the asterisks on the right of the coefficients. The datasets are clearly positively related. Given this, I also test the hypothesis that the two datasets move one-for-one, that is, that the slope coefficient equals one, with significance denoted by the asterisks to the left of the coefficient estimates. In only one case is this hypothesis not rejected. Loosely speaking, the APRA lending figures tend to vary more than the algorithm figures (i.e. coefficients greater than one), and the APRA borrowing figures tend to vary less (i.e. coefficients less than one). Correlations between the two datasets vary between 0.4 and 0.9, with little discernible difference for the APRA lending and borrowing datasets. This similarity in correlations may indicate that repo activity through Austraclear is correlated with repo activity through other infrastructure.
| Entity and year level | Entity level | Year level | ||||||
|---|---|---|---|---|---|---|---|---|
| Lending | Borrowing | Lending | Borrowing | Lending | Borrowing | |||
| Intercept | 0.533*** (0.07) |
0.440*** (0.05) |
1.382** (0.55) |
1.618*** (0.34) |
5.178*** (0.89) |
3.779*** (0.70) |
||
| Slope | ***1.452*** (0.16) |
***0.519*** (0.07) |
***2.487*** (0.32) |
**0.757*** (0.11) |
***2.056*** (0.22) |
0.983*** (0.13) |
||
| Correlation | 0.45 | 0.41 | 0.69 | 0.65 | 0.90 | 0.85 | ||
| R squared | 0.21 | 0.17 | 0.47 | 0.43 | 0.80 | 0.73 | ||
| Sample size | 309 | 304 | 69 | 69 | 24 | 24 | ||
|
Notes: **p < 0.05, ***p < 0.01; asterisks on the left of slope coefficients test whether coefficients equal one; OLS standard errors in parentheses Sources: APRA; ASX; Author's calculations; RBA |
||||||||
Unfortunately it is not possible to precisely account for each difference between the APRA and algorithm data, which must be kept in mind for the analysis in Section 5. Nevertheless, there is widespread ownership of Austraclear accounts across entities active in the Australian financial system (including many related to branches and subsidiaries of foreign banks). These entities have some incentive to use Austraclear rather than ICSDs owing to Austraclear's ability to simultaneously settle securities against domestic central bank currency. Moreover, for AGS and SGS repos, the algorithm and APRA series display similar trends across time. Taking everything into account, it seems reasonable to interpret the algorithm data as capturing the short-term domestic interbank repo market, acknowledging that this omits repos transacted through foreign infrastructure. This corresponds to the typical definition of the Australian unsecured interbank market, which only includes loans that are transacted through RITS.
5. The Australian Repo Market Microstructure
Now that we have a database of repo market transactions that is confirmed to be reasonably accurate, I examine the repo market microstructure implied by these data. The data cover the segment of the short-term (i.e. two weeks or less) repo market that is transacted through Austraclear. As discussed in Section 4, it seems reasonable to view this segment as the domestic interbank market, loosely defining all financial institutions as banks, and excluding from this definition repos involving banks with little presence in Australia. By comparison, previous published RBA analysis of the repo market adopts a broader scope more in line with activity reported to APRA. It is also worth reminding readers that the data in this section cover windows of September and October, which may not be representative of repo activity in other parts of the year, although the APRA data do not indicate much quarter-on-quarter volatility. Notwithstanding, there is some evidence that activity in short-term repos declines at quarter ends. On average, the value of detected repos outstanding declines 10 per cent in the two weeks encompassing each quarter end, relative to the value of detected repos the week before and the week after these two weeks.
In the following analysis, detected repos with particular characteristics are sometimes excluded to reduce the potential influence of false positives or of repos that are not representative of the information being conveyed. For example, when analysing spreads to the cash rate, repos open across the night after RBA Board meetings are typically excluded, because reference rates used by repo counterparties may diverge from the cash rate in those periods. Also, multiple-transaction repos are excluded where a small number of false positives could skew the information provided.[29]
As mentioned in the Introduction, the algorithm data treat securities loans – sometimes referred to as special repos – as a subset of repos. As opposed to ‘general collateral (GC) repos’, which are driven by the securities provider's demand for cash, securities loans are driven by the securities receiver's demand for the specific collateral. The securities receiver may, for example, be using the security to cover a short sale or to temporarily increase its inventories. In Australia, securities borrowers typically provide cash to collateralise the securities loan, which makes their transactions difficult to distinguish from other types of repos. This distinction can also be difficult conceptually, because there is likely some element of demand for cash in a typical securities loan, and of demand for the securities received in a GC repo. Throughout the following analysis the term ‘repo’ includes securities loans to the extent they satisfy the interest rate bounds, and ‘lender’ and ‘borrower’ always refer to the provider and receiver of cash (respectively).
5.1 Market Size, Collateral Types, Interest Rates and Maturities
The algorithm data reveal many repo characteristics not observable in previously available datasets. This section starts by describing the aggregate detected market, then analyses distributions of important variables such as collateral types, maturities (measured as number of days open) and interest rates. This informs us about, for example, the role that certain types of securities perform in our financial system, and the degree to which monetary policy transmits into other interbank rates.
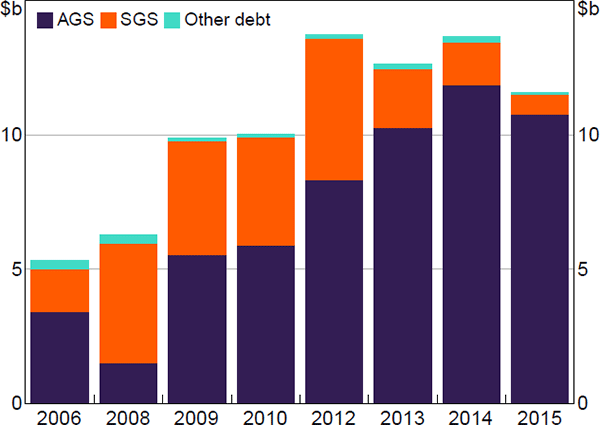
Between 2006 and 2015 the market size grew from around $5 billion to around $12 billion, measured by the value of outstanding positions on a typical night (Figure 4). In 2008, the SGS repo market was larger than the AGS repo market. Garvin, Hughes and Peydró (forthcoming) show that the repo market expanded substantially during the 2008 window, which captures the period surrounding the Lehman Brothers collapse, and the growth was primarily in SGS repos. They attribute this to increased demand for repo alongside a relative scarcity of AGS. In later years the proportion of the market against SGS declined, and in 2015 was less than a tenth the size of the AGS repo market. Throughout the full sample there is relatively little activity in repos against other-debt collateral, although any repos against privately-issued discount securities would not be captured (see Section 4).
Notes: September and October only; algorithm run with 14-day maturity cap; averaged across all nights excluding first and last two weeks each window
Sources: ASX; Author's calculations
Table 7 reports the ten issuers whose debt securities are most commonly used as repo collateral, and how many repo counterparties (i.e. number of Austraclear accounts) use that collateral. Aside from the Australian Government, the most prevalent issuers are the Queensland and NSW state governments, followed by the Victorian and Western Australian state governments. The most used other-debt collateral is issued by two supranationals and two German development banks. Collateral types tend to be broadly accepted – all in the table are provided by at least 16 different borrowers and accepted by at least 16 different lenders, with higher numbers for the more prevalent types. Two private sector entities rank twelfth and thirteenth (not shown in the table) with around 50 detected repos each.
Focusing on the 2015 window, the market does not appear to concentrate in particular ISINs within the AGS category of collateral (Table 8). Of the 32 ISINs on issue at some point in the window, all bonds and all but 1 treasury note appear in repos at least once. Each (non-indexed) treasury bond ISIN is used in at least 6 repos and each treasury indexed bond ISIN is used in at least 16 repos. Treasury bond ISINs tend to be favoured over other AGS ISINs, likely related to their long tenor and the large quantity on issue.
| Issuer | Detected repos | Borrowers | Lenders |
|---|---|---|---|
| Australian Government | 15,879 | 59 | 62 |
| Queensland Treasury Corporation | 2,894 | 48 | 54 |
| New South Wales Treasury Corporation | 2,278 | 48 | 51 |
| Treasury Corporation of Victoria | 859 | 40 | 45 |
| Western Australian Treasury Corporation | 849 | 47 | 43 |
| European Investment Bank | 309 | 29 | 32 |
| KFW Banking Group (Germany) | 271 | 27 | 28 |
| South Australian Financing Authority | 170 | 26 | 36 |
| Landwirtschaftliche Rentenbank (Germany) | 119 | 21 | 22 |
| International Bank for Reconstruction and Development | 79 | 16 | 16 |
|
Note: Algorithm run with 14-day maturity cap Sources: ASX; Author's calculations |
|||
| Treasury bonds | Treasury indexed bonds | Treasury notes | |
|---|---|---|---|
| Number of ISINs on issue | 22 | 7 | 3 |
| Lowest frequency of an ISIN | 6 | 16 | 0 |
| Median ISIN frequency | 121 | 30 | 3 |
| Highest frequency of an ISIN | 213 | 37 | 4 |
|
Notes: Algorithm run with 14-day maturity cap; repos with more than two transactions excluded Sources: ASX; Author's calculations |
|||
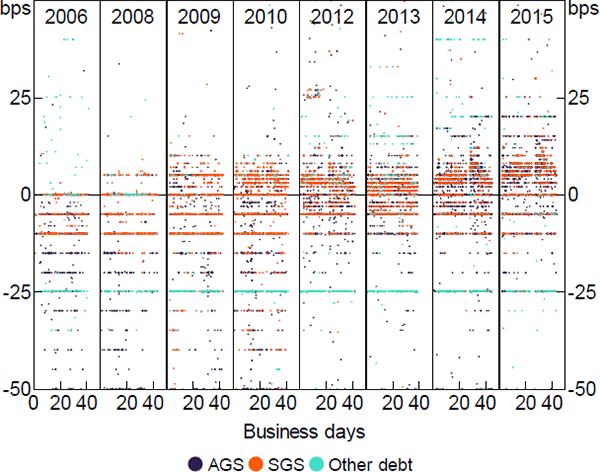
Figure 5 plots the interest rate spread to the cash rate for every repo, excluding those open across RBA policy decisions. The position on the x-axis represents the business day and time the first transaction in the repo was settled. For example, a point in the 2015 panel at (20.5, –10) would represent a repo 20.5 business days into the 2015 September–October window – that is, at 12 pm on the 21st day – at 10 basis points below the cash rate. When plotted observations overlap they may not all be visible in the figure; the layering from least visible to most visible reflects their frequency – AGS, SGS, then other-debt collateral.
At each point in time rates tend to be dispersed in a 50 basis point range, even within collateral types. The cross-sectional variance overshadows the market-wide variance across days, although the distribution of spreads tightens from 2006 to 2015. This could relate to, for example, a shift towards shorter maturities, discussed later in this section, a change in the dispersion of loan sizes, or changes in the role of the market. Spreads tend to be concentrated at multiples of 5 basis points, indicating common use of the cash rate as a reference rate.
Around 42 per cent of the positive spreads in Figure 5 are overnight repos, which suggests that access by these borrowers (i.e. cash receivers) to the unsecured market was constrained; otherwise they would borrow unsecured at a lower rate and without any collateral obligation. There is also a cluster of repos at 25 basis points below the cash rate. These repos are likely securities loans, consistent with the relatively high frequency of non-government collateral.[30] Market intelligence also indicates that rates on securities loans are sometimes negotiated from a reference point of 25 basis points below the cash rate.
Notes: September and October only; algorithm run with 14-day maturity cap; repos spanning policy decisions excluded
Sources: ASX; Author's calculations; RBA
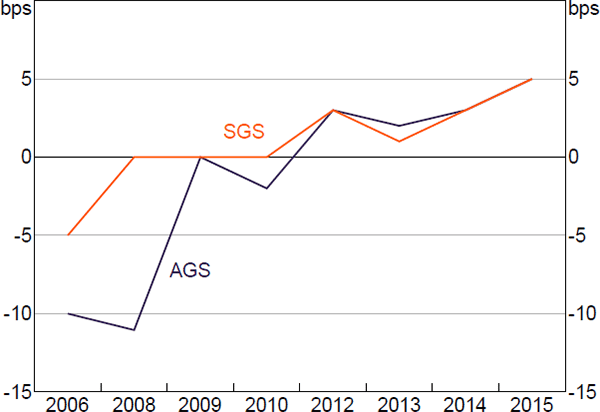
Figure 6 plots the pattern of increasing spreads evident in Figure 5, displaying the median spread each year for AGS and SGS repos. Becker, Fang and Wang (2016) and Becker and Rickards (2017) also note increasing market-wide repo rates towards the end of this sample, finding evidence that demand for Australian dollar funds from non-resident borrowers has been contributing to these rises. A noticeable deviation between AGS and SGS spreads occurs in 2008. Garvin et al (forthcoming) conclude that this is at least partly driven by demand for AGS (i.e. the highest quality collateral) alongside a relative scarcity on issue.
Notes: September and October only; algorithm run with 14-day maturity cap; repos spanning policy decisions excluded; one high turnover borrower-lender pair excluded
Sources: ASX; Author's calculations; RBA
For maturities of 14 days or less, there is little evidence of a yield curve (Figure 7). Only repos with rounded interest rates are displayed, because these are more likely to have terms negotiated at the start of the repo rather than being rolled over, and therefore the time between the first and last transactions is more likely to represent overall maturity rather than the sum of several rolled over maturities.[31] Spreads for 1-, 2- and 3-day maturities tend to be relatively flat, and spreads at 14 days tend to tick up. Nevertheless, there is no clear systematic trend evident.
Figure 8 defines maturity as business nights between the first and last transaction, excludes repos most likely to be rollovers, and displays the market share at each maturity. Between 2006 and 2015 the market shifts towards overnight maturities. In all displayed years there is substantial market share at one-week maturity (i.e. five business days); however, this declines from around 30 per cent in 2006 to be below 25 per cent in every subsequent year in the sample (including those not displayed). Excluded from Figure 8 is a borrower-lender pair that in 2015 contributes a disproportionate share of turnover; including them makes the overnight market share above 50 per cent.
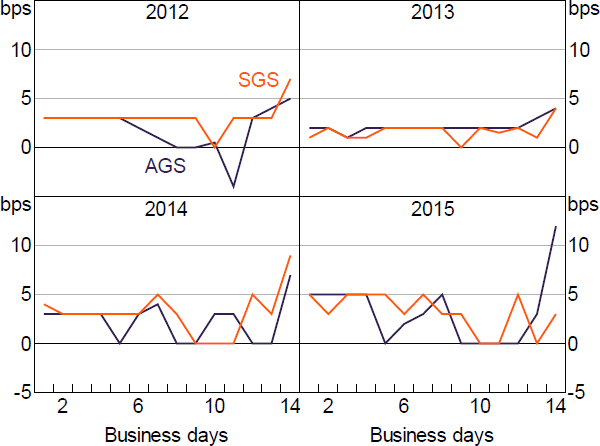
Notes: September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions, spanning policy decisions or with non-rounded interest rates excluded; one high turnover borrower-lender pair excluded
Sources: ASX; Author's calculations; RBA
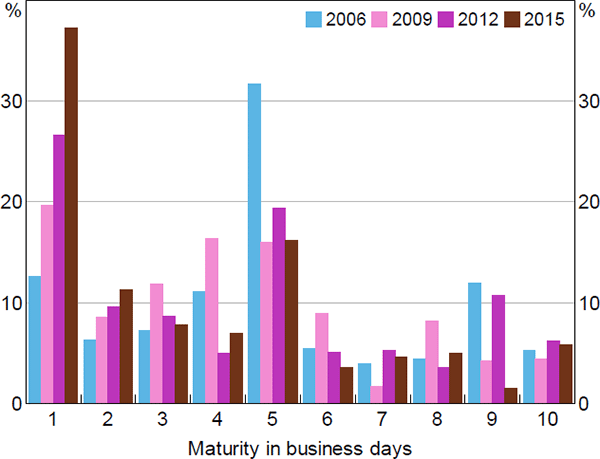
Notes: September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions or with non-rounded interest rates excluded; one high turnover borrower-lender pair excluded; averaged across all nights excluding the first and last two weeks of each window
Sources: ASX; Author's calculations
For an indication of whether repos occur at maturities above two weeks, I also run the algorithm with a 61-day maturity cap. For these longer maturity repos, turnover is a more useful measure of activity than share of outstanding positions.[32] In 2006, there is a pronounced spike in turnover detected at 30 days (retaining non-business days) that comprises 12 per cent of total turnover. In 2015, aside from a small spike of around 0.5 per cent of turnover at 21 days, activity at maturities longer than 14 days is scarce.[33]
5.2 Loan-level Regressions of Repo Rates
Next I analyse repo interest rates by regressing them on other repo characteristics. This allows formal tests of whether repo rates vary with other repo characteristics while holding potentially confounding variables constant. Treating each detected repo from 2012 to 2015 as an observation, I regress interest rates on appropriate transformations (specified in Table 9) of the following variables: the quantity of lender's OMO borrowing that morning;[34] the size of the repo (i.e. cash lent); a dummy indicating whether the lender subsequently sold the collateral it received while the repo was still open, indicative of the repo being used to cover a short sale;[35] dummies for maturity buckets; dummies for collateral types; and a dummy indicating whether the collateral was a reference bond in the futures market.[36]
Individual repos are indexed by i, such that the space of i includes dimensions for lender l, borrower b and day d (and therefore also year y), with lender and borrower measured at the CSD account level. The set of explanatory variables is labelled X. I estimate two equations:
and
Equation (2) includes day fixed effects to control for any day-to-day fluctuations in market-wide rates. Equation (3) includes day fixed effects and borrower*lender*year fixed effects, focusing on variance in rates within borrower-lender pairs each year. For example, if a correlation exists among a set of repos that each involve different lenders or borrowers (on the same day), Equation (2) would detect it and Equation (3) would not. Equation (3) excludes rate differentials across different counterparties, focusing on, for example, whether repos between the same two counterparties have higher rates when the loans are larger. Equation (3) is therefore more robust to omitted variable bias driven by unobserved characteristics that vary across counterparties.
Table 9 reports the coefficient estimates. Notable findings are:
- Consideration: Loan size has a highly significant and positive relationship across both specifications. When a loan doubles in size, the rate increases by around 0.8 basis points. Possible explanations could include a thinner market for larger loans that tilts market power towards the lender, or compensation to the lender for a higher concentration of counterparty risk in that borrower.
- Short sale: Repos appearing to cover short sales (likely to be securities loans) have rates 1.3 basis points lower than others. The sign is as expected, with cash providers compensating borrowers for receiving the collateral. The dummy is a proxy and may result in underestimates if it also picks up repos used for other purposes.
- Maturities: The Equation (2) estimates are consistent with a term premium, that is, estimated rates are higher for longer maturity buckets. However, the Equation (3) estimates reveal that this is not true when holding the counterparties constant.
- Collateral type: SGS repos tend to have a rate around 1 basis point higher than AGS repos. Bartolini et al (2011) find a similar but wider disparity in the United States – in data up to 2006, rates on repos against Treasury securities are around 5 basis points lower than rates on repos against agency securities. Other-debt repos tend to have a rate around 6 basis points lower than AGS repos. These repos potentially comprise more securities loans.
- Futures collateral: These repos have statistically significantly higher rates by 0.7 basis points. This is consistent with the arbitrage position discussed in Wakeling and Wilson (2010) and Becker et al (2016). Specifically, banks short futures and buy the underlying bonds to take advantage of the futures price being above the price of the underlying bonds. Banks can fund the bond purchase by borrowing through repos using the bond as collateral, putting upward pressure on rates for these repos.
| Equation (2) | Equation (3) | |
|---|---|---|
| Lender's OMO (IHS, $b)(a) | 4.882 (3.75) |
−0.536 (0.47) |
| Consideration (log $m) | 0.890*** (0.30) |
1.136*** (0.20) |
| Short sale (D) | −2.53 (1.66) |
−1.264** (0.48) |
| Maturity 2–7 days (D) | 1.960* (0.98) |
0.262 (0.33) |
| Maturity 8–14 days (D) | 2.913** (1.21) |
0.132 (0.57) |
| SGS collateral (D) | 1.215** (0.56) |
0.960*** (0.32) |
| Other-debt collateral (D) | −6.136 (4.97) |
−6.189* (3.34) |
| Collateral referenced in futures (D) | 0.596 (0.38) |
0.704*** (0.26) |
| Fixed effects | day | day and borrower*lender*year |
| R squared | 0.081 | 0.471 |
| Number of observations | 15,955 | 15,695 |
|
Notes: *p < 0.1, **p < 0.05, ***p < 0.01; standard errors in parentheses clustered at the lender account level (42 clusters); state government entities removed from regressions; D denotes a dummy variable (a) IHS refers to the inverse hyperbolic sine transformation, similar to a log transformation but capable of transforming zeros Sources: ASX; Author's calculations; RBA |
||
5.3 Market Structure in 2015
In this section I analyse the distribution of counterparty relationships in the repo market. The algorithm data identify the borrower and lender to each position. This permits analysis of: a) the relative activity of each entity; b) the network of repo positions; and c) how repo rates vary across the market network. Since these market characteristics vary over the full sample, I focus on the most recent data window comprising September and October 2015. Note that these data do not capture repos through foreign infrastructure, which could, for example, add extra links to the market network as implied by the algorithm data.
Because institutions often hold multiple Austraclear accounts, for this section I group accounts into ‘entities’, combining activity across any accounts held under the same parent company. The exception is when the account name indicates it is used on behalf of clients, in which case I label that account, grouped together with any other client accounts under the same parent company, as being a client entity.[37] Two of the client entities include accounts related to ICSDs. Entities other than client entities and state governments are classified as domestic or foreign, based on the location of their parent company. Intra-entity repos are excluded.
Figure 9 displays each entity's share of total repo turnover in 2015, measured as the sum of the cash side of all repos in the window regardless of maturity. Each horizontal bar is an entity; the left and right panels display that entity's lending and borrowing turnover respectively. Turnover is highly skewed towards a single borrower-lender pair, contributing around half of the total. Aside from this pair, the bulk of turnover is distributed across 15 to 20 entities, most of whom both lend and borrow. Five of the six most active of these entities are Australian, and most of the remaining activity is by foreign and client entities.
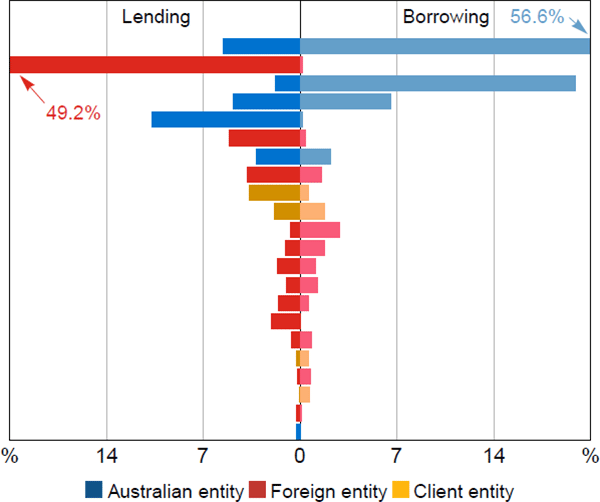
Notes: Algorithm run with 14-day maturity cap; entities ordered by combined borrowing and lending turnover; excludes repos with state government entities
Sources: ASX; Author's calculations
Figure 10 illustrates the market as a network. Each node is an entity, coloured by domicile (or client). The shape represents its average net overnight position across all counterparties – circles are net lenders, squares are net borrowers, and the size of the shape represents the value of their average net overnight position (using a nonlinear scale). Each (undirected) edge represents a bilateral position, with the thickness representing the total gross value of lending and borrowing between that pair (also using a nonlinear scale).
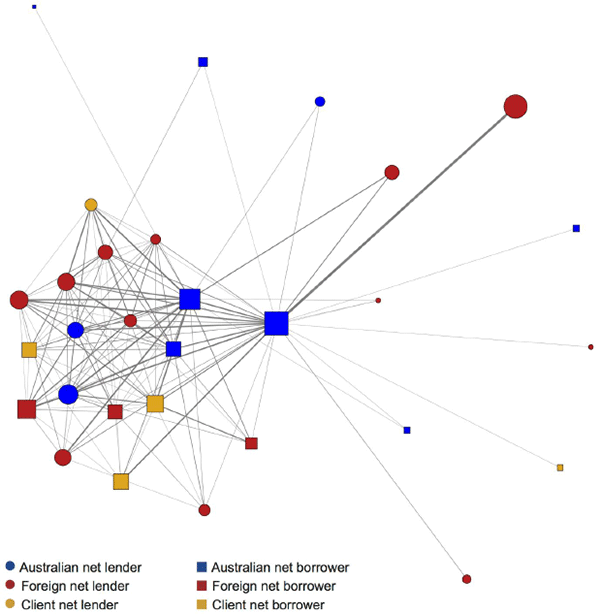
Notes: Node size represents average overnight position netted across all counterparties; edge width represents average gross overnight position between counterparty pair; algorithm run with 14-day maturity cap; excludes repos with state government entities
Sources: ASX; Author's calculations
There is a distinct core-periphery split.[38] Around a third of entities are ‘periphery’ entities that are not linked with each other and have only one or two counterparties. Around two-thirds are ‘core’ entities, each with five or more counterparties in the core, plus counterparties in the periphery. The core is well integrated; most have more than ten counterparties. On the other hand, if data in this sample are representative of the current market structure, periphery entities are somewhat segmented and their market access might easily be disrupted if there are problems with their one or two core counterparties. The market structure seems inconsistent with core entities' primary activity being intermediation for the periphery, given core entities' relatively large net positions. Among the core, the pattern is more consistent with market ‘churn’ related to entities seeking other entities with which to offset day-to-day surpluses and deficits in liquidity and securities holdings.
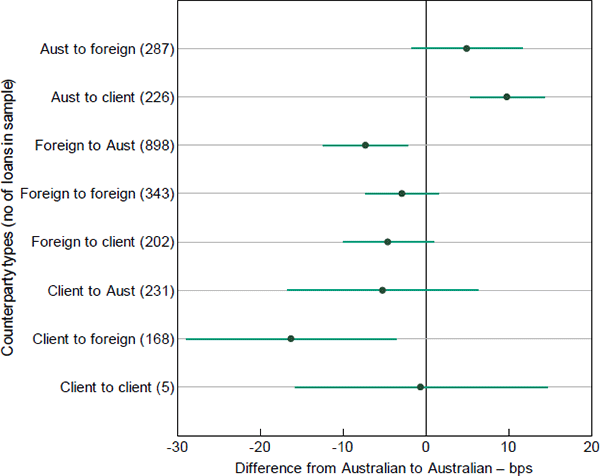
Repo rates tend to vary across counterparties. Figure 11 plots the estimated difference in rates between different lender and borrower types, with 95 per cent confidence intervals, relative to rates on repos between Australian lenders and Australian borrowers. Specifically, the coefficients are from a re-estimation of Equation (2) on 2015 data with X comprising: eight domicile dummy variables representing the nine types of lender-borrower combinations, with loans from Australian lenders to Australian borrowers as the baseline; dummies for 2–7 and 8–14 day maturity buckets; and dummies for collateral types. Rates are highest for repos from Australian lenders to client borrowers, in line with Becker and Rickards' (2017) explanation that non-residents' demand for funding has put upward pressure on repo rates in recent years. Overall, rates charged by Australian lenders tend to be higher than rates charged by other lenders. The lowest rates are from client lenders to foreign borrowers.
Notes: With day fixed effects and other control variables; clustered standard errors
Sources: ASX; Author's calculations
There is some evidence of collateral rehypothecation in the algorithm data. Potential rehypothecation can be identified as instances of an entity receiving collateral as a lender, then using securities of the same ISIN as collateral for borrowing later on the same day. Around 5 per cent of the two-transaction repos detected are followed by potential rehypothecation (after removing overlapping instances).
5.4 Haircuts
A repo haircut (sometimes called an initial margin) is defined as the proportion by which the collateral value exceeds the cash lent:
Haircuts are intended to keep the lender fully collateralised should the market price of the securities move adversely. The data may therefore inform us about how repo counterparties manage their risk. Under global conventions, haircuts are higher for securities with more volatile prices, which have greater potential to change in price while the repo is open. For current RBA lending in OMO, the lowest haircut is 1 per cent, corresponding to AGS and SGS, and the highest haircut is 20 per cent, corresponding to asset-backed securities. For securities loans (which likely describes some of the detected repos) we may expect haircuts as defined by Equation (4) to be negative. This would protect the securities lender, rather than the provider of the cash collateral, against changes in the securities price.
To obtain implied haircuts from the algorithm repo data, the repo dates and collateral ISINs can be aligned with data on securities market prices. I do this using the (mid) closing prices each settlement day for all AGS and SGS repos in the 2012 to 2015 windows, with data from the RBA and Yieldbroker. For multiple-transaction repos, the implied haircut is measured using only the first transaction. Market intelligence indicates that some repos are negotiated the day before the first-leg settlement, which may result in some misalignment between the repo and securities price data, adding noise to the haircut measure I construct. Notwithstanding this, this measure has lower variance than a measure that uses securities prices from a day earlier.
Implied haircuts tend to be scattered around zero – in each window the mean haircut is less than 0.1 per cent in absolute value (Figure 12). In 2014 and 2015 there are clusters around 1 and 2 per cent, which reflect only a small subset of entities. Implied haircuts are often negative. The negative haircuts are spread across various counterparties, ISINs and settlement times, and, gauged by the incidence of rounded interest rates (discussed in Section 3.3), do not contain a noticeably larger proportion of false positives. These may comprise a higher proportion of securities loans.
Note: Algorithm run with 14-day maturity cap
Sources: ASX; Author's calculations; RBA; Yieldbroker
To further investigate implied haircut patterns I regress Equations (2) and (3) from Section 5.2 replacing ratei with haircuti and limiting the sample to AGS and SGS repos between 2012 and 2015. I use the same explanatory variables X, but also include the repo rate in basis points. If haircuts represent value to the lender and a cost to the borrower, we may expect a negative relationship with repo rates, as counterparties negotiate by raising one and lowering the other. To lenders, higher haircuts reduce counterparty risk and temporarily increase liquid asset holdings. To borrowers, haircuts may represent the cost of capital for securities financing, being the gap between the funds obtained by borrowing against the security and the funds required to purchase it (e.g. Ashcraft, Gârleanu and Pedersen 2011).
Table 10 reports the estimates. Of the 16 reported coefficients, 1 is significant at 90 per cent confidence, therefore likely a type I error.[39] There is no significant relationship between haircuts and repo rates, indicating they are not simultaneously negotiated. The coefficient on the short sale dummy is also not significant, which is at odds with the notion that the negative haircuts correspond to securities loans.
| Equation (2) | Equation (3) | |
|---|---|---|
| Repo rate (bps) | 0.078 (0.38) |
0.060 (0.08) |
| Lender's OMO (IHS, $b)(a) | 0.014 (0.04) |
0.006 (0.04) |
| Consideration (log $m) | 0.038 (0.03) |
−0.001 (0.00) |
| Short sale (D) | −0.015 (0.03) |
−0.009 (0.01) |
| Maturity 2–7 days (D) | −0.021 (0.05) |
0.026* (0.01) |
| Maturity 8–14 days (D) | −0.011 (0.04) |
0.011 (0.02) |
| SGS collateral (D) | −0.022 (0.02) |
0.014 (0.01) |
| Collateral referenced in futures (D) | −0.020 (0.02) |
0.011 (0.04) |
| Fixed effects | day | day and borrower*lender*year |
| R squared | 0.143 | 0.537 |
| Number of observations | 14,858 | 14,596 |
|
Notes: *p < 0.1, **p < 0.05, ***p < 0.01; standard errors in parentheses clustered at the lender account level (42 clusters); state government entities and haircuts above 5 per cent in absolute value removed from regressions; D denotes a dummy variable (a) IHS refers to the inverse hyperbolic sine transformation, similar to a log transformation but capable of transforming zeros Sources: ASX; Author's calculations; RBA |
||
5.5 Intraday Timing Patterns in 2015
The algorithm data also provide detailed information on the intraday timing of interbank repo settlements. Importantly, the algorithm data contain the transactions' settlement times, which could differ from the times at which the counterparties negotiated the repos. As discussed in the previous section, some repos are likely negotiated the day before settlement.
Figure 13 illustrates the variance in repo volumes, values, spreads and maturities within an average day in the 2015 window. Some relatively low-value repos tend to occur in the early morning. A drop in volume and value occurs around 4.30 pm. Brassil et al (2016) show that unsecured lending peaks during the ‘close’ session between 4.30 pm and 5.15 pm, when banks acquire information on how the processing of SWIFT customer payments has affected their liquidity position. Given their findings, Figure 13 indicates a substitution from the repo to the unsecured market at this time, and the pick-up in repo values between 4.30 pm and 5.30 pm may reflect entities turning back to the repo market to find funds not sourced in the unsecured market.
Average spreads rise throughout the day, although the pattern is not robust after controlling for other variables such as lender and borrower characteristics. The pick-up in spreads after 6 pm is driven by a small number of repos and potentially not representative of the overall market. Average maturities decline gradually from 4.5 days around 9 am to 1 day after 6 pm. Consistent with the discussion in the previous paragraph, this could be indicative of early market activity being driven by predictable funding needs, and late activity comprising more short-term needs resulting from unexpected liquidity imbalances.
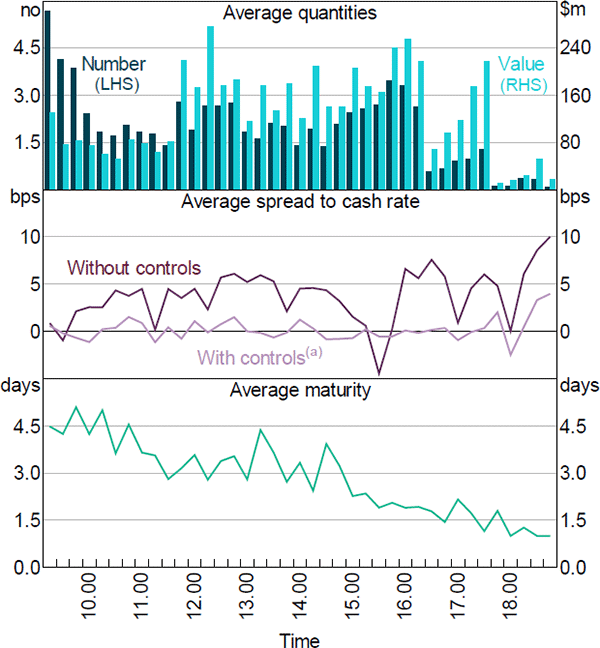
Notes:
September and October only; algorithm run with 14-day maturity cap; repos with more than two transactions or spanning policy decisions excluded; one high turnover borrower-lender pair excluded
(a) Average of residuals from regressing spreads on maturity and dummies for day, security type (AGS, SGS and other) and borrower-lender pairs
Sources: ASX; Author's calculations; RBA
6. Conclusion
This paper provides an algorithm for extracting loan-level repo data from securities transactions data and uses the algorithm for a preliminary loan-level analysis of the Australian repo market. Related algorithms are commonly used for loan-level analysis of unsecured interbank markets around the world. Yet, until now, there has been little access to loan-level data on repo markets.
Assessment of the algorithm indicates that around 97 per cent of the detected loans are actual repos. The algorithm data detect a smaller market than reported in prudential data, likely in part reflecting repos with offshore entities that are reported to the prudential regulator but do not appear in the transactions data. Correlations between the two datasets are around 0.5.
I also provide the first analysis of the Australian repo market microstructure, covering several two-month samples between 2006 and 2015. Over these years the market size grew, the distribution of interest rates drifted up and tightened, and there was a shift towards shorter maturities. Interest rates tend to depend on loan size and the types of counterparties, but not maturity. In 2015, turnover is skewed towards a highly active pair, and the market network structure is split between a tightly integrated core and a segmented periphery that each deal with only one or two counterparties. Repo haircuts do not display obvious patterns, appearing randomly distributed around zero.
References
Acharya VV and O Merrouche (2013), ‘Precautionary Hoarding of Liquidity and Interbank Markets: Evidence from the Subprime Crisis’, Review of Finance, 17(1), pp 107–160.
Adrian T, B Begalle, A Copeland and A Martin (2014), ‘Repo and Securities Lending’, in M Brunnermeier and A Krishnamurthy (eds), Risk Topography: Systemic Risk and Macro Modeling, National Bureau of Economic Research Conference Report, The University of Chicago Press, Chicago, pp 131–148.
Afonso G, A Kovner and A Schoar (2011), ‘Stressed, Not Frozen: The Federal Funds Market in the Financial Crisis’, The Journal of Finance, 66(4), pp 1109–1139.
Arciero L, R Heijmans, R Heuver, M Massarenti, C Picillo and F Vacirca (2016), ‘How to Measure the Unsecured Money Market: The Eurosystem's Implementation and Validation Using TARGET2 Data’, International Journal of Central Banking, 12(1), pp 247–280.
Armantier O and A Copeland (2012), ‘Assessing the Quality of “Furfine-Based” Algorithms’, Federal Reserve Bank of New York Staff Report No 575.
Ashcraft AB and D Duffie (2007), ‘Systemic Illiquidity in the Federal Funds Market’, The American Economic Review, 97(2), pp 221–225.
Ashcraft A, N Gârleanu and LH Pedersen (2011), ‘Two Monetary Tools: Interest Rates and Haircuts’, in D Acemoglu and M Woodford (eds), NBER Macroeconomics Annual 2010, 25, University of Chicago Press, Chicago, pp 143–180.
Bartolini L, S Hilton, S Sundaresan and C Tonetti (2011), ‘Collateral Values by Asset Class: Evidence from Primary Securities Dealers’, The Review of Financial Studies, 24(1), pp 248–278.
Becker C, A Fang and JC Wang (2016), ‘Developments in the Australian Repo Market’, RBA Bulletin, September, pp 41–46.
Becker C and P Rickards (2017), ‘Secured Money Market Transactions: Trends in the Australian Repo Rate’, Paper presented at the 22nd Melbourne Money and Finance Conference ‘Evolutionary Trends in the Australian Financial Sector’, Hosted by the Australian Centre for Financial Studies, Melbourne, 10–11 July.
Brassil A, H Hughson and M McManus (2016), ‘Identifying Interbank Loans from Payments Data’, RBA Research Discussion Paper No 2016-11.
Brassil A and G Nodari (2018), ‘A Density-Based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market’, RBA Research Discussion Paper No 2018-01.
Copeland A, D Duffie, A Martin and S McLaughlin (2012), ‘Key Mechanics of the U.S. Tri-Party Repo Market’, Federal Reserve Bank of New York Economic Policy Review, 18(3), pp 17–28.
Copeland A, A Martin and M Walker (2014), ‘Repo Runs: Evidence from the Tri-Party Repo Market’, The Journal of Finance, 69(6), pp 2343–2380.
CPMI (Committee on Payments and Market Infrastructures) (2016), Statistics on Payment, Clearing and Settlement Systems in the CPMI Countries, CPMI Papers No 155, Bank for International Settlements, Basel.
ECB (European Central Bank) (2015), ‘Euro Money Market Survey’, September.
Fuhrer LM, B Guggenheim and S Schumacher (2016), ‘Re-Use of Collateral in the Repo Market’, Journal of Money, Credit and Banking, 48(6), pp 1169–1193.
Furfine CH (1999), ‘The Microstructure of the Federal Funds Market’, Financial Markets, Institutions & Instruments, 8(5), pp 24–44.
Garvin N, D Hughes and J-L Peydró (forthcoming), ‘Repo and Unsecured Interbank Markets under Stress: Evidence from Transaction-Level Data’, RBA Research Discussion Paper.
Gorton G and A Metrick (2012), ‘Securitized Banking and the Run on Repo’, Journal of Financial Economics, 104(3), pp 425–451.
Kovner A and D Skeie (2013), ‘Evaluating the Quality of Fed Funds Lending Estimates Produced from Fedwire Payments Data’, Federal Reserve Bank of New York Staff Report No 629.
Krishnamurthy A, S Nagel and D Orlov (2014), ‘Sizing up Repo’, The Journal of Finance, 69(6), pp 2381–2417.
Kuo D, D Skeie, J Vickery and T Youle (2013), ‘Identifying Term Interbank Loans from Fedwire Payments Data’, Federal Reserve Bank of New York Staff Report No 603, rev August 2014.
Mancini L, A Ranaldo and J Wrampelmeyer (2016), ‘The Euro Interbank Repo Market’, The Review of Financial Studies, 29(7), pp 1747–1779.
Rempel M (2016), ‘Improving Overnight Loan Identification in Payments Systems’, Journal of Money, Credit and Banking, 48(2-3), pp 549–564.
Wakeling D and I Wilson (2010), ‘The Repo Market in Australia’, RBA Bulletin, December, pp 27–35.
Acknowledgements
I would like to thank ASX staff Tim Hogben and Wayne Jordan for help with the data, and Chris Becker, Matt Boge, Anthony Brassil, Michele Bullock, Jon Cheshire, Duke Cole, Jenny Hancock, David Hughes, Mark Manning, Yasaman Naghiloo, David Olivan and John Simon for input, feedback and assistance. The views in this paper are my own and do not necessarily reflect the views of the Reserve Bank of Australia. Any errors are my own.
Footnotes
‘Repo’ is short for ‘repurchase agreement’. A repo is similar to a securities sale paired with a subsequent repurchase. [1]
This figure focuses on the overnight markets because the overnight unsecured market is the target of monetary policy, but it does not necessarily represent activity at other maturities. Section 5.1 shows that between 2006 and 2015, there was a substantial shift in repo market activity towards overnight maturity. [2]
Securities loans are sometimes referred to as special repos, as opposed to general collateral (GC) repos, and are driven by the collateral receiver's demand for the particular collateral received, for example, to cover a short position in those securities. Since they are often collateralised by cash, they can be difficult to distinguish from other repos. This paper treats securities loans as a subset of repos [3]
Copeland et al (2012) describe tri-party repo infrastructure in the United States. [4]
Discount securities (i.e. securities without coupon payments such as bank bills) issued by private entities are excluded from the data prior to analysis, so these figures do not include any repos collateralised by them. [5]
With minor modifications the algorithm would work if only the settlement day is observable, but would have more difficulty detecting some repos that involve more than one transaction on the same day. [6]
In some cases, longer-maturity sets may be selected over others because the crosschecking required would substantially increase computing time. This could be modified if computing capacity imposed less constraint. [7]
The number of possible combinations among N transactions is 2N. [8]
Modifications of the standard dynamic programming solution to the subset sums problem were found to be inefficient in this setting. [9]
In the code in the online supplementary information, this parameter is the ‘matrix.max’ argument in the top-level ‘repo.alg.F’ function. [10]
There is little evidence in the data that intraday repos occur at other interest rates or with a fixed fee. [11]
In practice, only the locations (e.g. row numbers) of transactions are stored. [12]
Alternatively, it would be straightforward to choose from overlapping repos using other characteristics such as implied interest rate or settlement times. [13]
For each temporary maximum transaction number, it is not necessary to iterate through the lower values of k referred to in the above description of the iterative method. However, the improvements in computing time from removing these iterations are small, and additional detections are possible given the constraints imposed on candidate vector lengths. [14]
Some statistics on Austraclear are available in CPMI (2016). [15]
The periods captured are in part determined by data availability. [16]
The code provided in the online supplementary information has an option to switch off this part of the algorithm, or to switch off multiple-transaction repo detection completely. [17]
Wakeling and Wilson (2010) report that there is no fixed convention for collateral top-ups in Australia. The transactions data are checked for signs of collateral swaps – that is, while a repo is open, a provision of a new type of collateral and a return of the original type – and no evidence for this behaviour is found. [18]
The Rempel (2016) approach has the advantage that the distribution of false detections can be estimated by repeating the exercise on many different data reshuffles. [19]
For example, if the cash rate is 4.5 per cent throughout a sample window, the standard bounds are 3.5 and 5.5 per cent, and the placebo bounds are −5.5 and −3.5 per cent. [20]
It is possible that securities lending occurs at negative interest rates. This would bias the estimated false detection rate upward. It is also possible that short-selling activity satisfies the algorithm conditions, because a short sale must typically be followed by the seller repurchasing the same securities to return to the securities lender (although the purchase may be from a different counterparty). [21]
The three years reported in Table 3 have higher false detection rates than all other years in the data. [22]
Only transactions between entities that appear in standard detected repos are retained for this exercise. [23]
This would also capture instances of the borrower replacing the collateral type during the life of the repo, if the original and replaced collateral had the same face value, and had different ISINs but the same general label. [24]
Note that these would be detected as two separate repos under the standard conditions if the considerations in the repayment transactions aligned with the two lending transactions plus interest. [25]
In an earlier version of the algorithm, the maturity was given higher priority than the number of transactions for multiple-transaction repos, and the number of repo detections was very similar. [26]
The APRA dataset in more aggregated form can be found in statistical table B3 ‘Repurchase Agreements and Stock Lending by Banks and Registered Financial Corporations’ at <https://www.rba.gov.au/statistics/tables/>. [27]
For this section I set the maturity cap at 61 days, the interest bounds at 1 percentage point either side of each window's cash rate range, and the transaction cap at 6. I use the longer maturity cap because repos of all maturities are reported to APRA. [28]
Section 3.3 estimates that repos with more than two transactions have a false detection rate of around 26 per cent, whereas repos with two transactions have a false detection rate of around 1 per cent. [29]
These include repos against all three collateral types, although the repos against AGS and SGS are partly hidden by the other-debt repos. [30]
Rounded interest rates have only zero decimals when measured in basis points with two decimal places. See Section 3.3.1 for further discussion. [31]
To illustrate this point, consider that a 60-day repo represents the same share of outstanding positions as 60 overnight repos of the same value. However, there are only 61 days in each data window, so we can only observe 60-day repos if they are initiated in the first day of the window. Therefore, while the share of overnight repos is calculated from many observations, the share of 60-day repos is calculated from a very small number of observations (and requires an upward adjustment to acknowledge this limited ability to observe). This 60-day share may not be representative of general activity, particularly given the possibility of false detections. It is therefore problematic to directly compare the market shares of repos that have large differences in maturities. [32]
These turnover shares are underestimates of the true values due to the issue discussed in the previous footnote. Still, the degree of underestimation depends primarily on the repo's maturity, so spikes in turnover share relative to shares at similar maturities are somewhat reliable indicators of greater activity. [33]
OMO borrowing is measured as funds received on that day from the Austraclear account that the RBA uses for OMO, also obtained from the Austraclear transactions data. The RBA typically carries out OMO at 9.20 am each morning. [34]
For this variable, Austraclear transactions with non-zero considerations that are not part of repos are interpreted as outright trades. They are only counted if they occur within two days of the first transaction of the repo. [35]
For each regression reported in this paper, repos that occur through separate transactions but are otherwise virtually identical – that is, same counterparties, settlement days, collateral type and interest rate – are aggregated into one repo to prevent estimates overweighting these repos. For the other analysis in this paper, aggregation of these repos would be less consequential. [36]
Client accounts are identified by the account name containing ‘nominee’, ‘client’, ‘custodian’ or an abbreviation of any of these. [37]
Brassil and Nodari (2018) discuss core-periphery structures in more detail with reference to the Australian unsecured interbank market. [38]
A confidence level of 90 per cent means that for every ten null hypotheses that are true, we would expect to falsely reject one of them. [39]