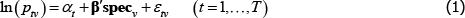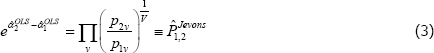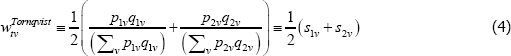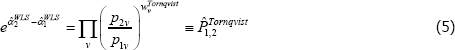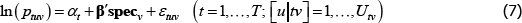RDP 2018-08: Econometric Perspectives on Economic Measurement 2. The Standard Model Needs Changing
July 2018
- Download the Paper 1,726KB
2.1 The Standard Model
The econometric model most commonly used to define the price measurement task descends from pioneering work by Court (1939). Using assumptions A1 to A4, it describes pricing behaviour in some market for differentiated product varieties. To distinguish it from a later model that will have many of the same characteristics, call it The Standard Model.
A1
where: ptv is the transaction price of variety v in time period or territory (place) t; αt is a fixed effect for t; β is a vector of parameters; and specv is a vector of observed variety specifications. Hence β′specv can be seen as a control for the effect of quality on prices. εtv is an error term.
A2 Across varieties the observations are independently and identically distributed.
A3 The errors are strictly exogenous. So
A4 Other technical conditions of regularity are satisfied, ruling out perfect multicollinearity and variables with infinite second moments.
For measurement, the interest is in the differences between the αt. For instance, if
t is for time, 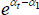 indexes a time series of the price level, holding quality constant. The series is useful for measuring inflation
and deflating nominal aggregates into real ones. If t is for territory,
indexes a time series of the price level, holding quality constant. The series is useful for measuring inflation
and deflating nominal aggregates into real ones. If t is for territory, 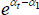 indexes a cross-section of purchasing power parities.
indexes a cross-section of purchasing power parities.
Special cases of The Standard Model shape many macro indicators. Hence, a lot of empirical macro research is linked to it somehow. Aside from variation in the concept behind t, the special cases differ along several dimensions:
- The market types vary. For instance, in official capacities The Standard Model has been applied to the rental market in the United States (Bureau of Labor Statistics 2017), the used car market in Germany (German Federal Statistical Office 2003), and the computer market in Australia (Australian Bureau of Statistics 2005). It can be applied to markets that are more broadly defined as well.
- The types of regressors in specv differ. In measurement handbooks the regressors are often variety attributes (International Labour Office et al 2004; International Labour Organization et al 2004; Eurostat 2013). In this case the model becomes ‘hedonic’. In some other cases the regressors are variety dummies and β′specv becomes a variety fixed effect (World Bank 2013).
-
The population of transacted varieties can be static, with no entry or exit, or it can be dynamic. The static case is special because t is definitionally uncorrelated with the regressors in specv. Including β′specv is thus irrelevant for defining the population price index. This is the classic setup in the prevailing stochastic approach to choosing index functions, described more fully in Section 3.3.
In measurement contexts more broadly, static populations are sometimes synthetic, in the sense that missing varieties are assumed to have hypothetical prices. Often the hypothetical prices correspond to predictions of T = 1 versions of The Standard Model (and where interest is not in the αt). This method is behind official price indices for mobile phones in the United Kingdom (Office for National Statistics 2014). Since modelling considerations then change, this paper is not about T = 1 cases, except where stated otherwise.
-
Still, the size of T can vary. Territory applications are often multilateral, so T ≥ 3,
as in versions that support official calculations of purchasing power parities (World Bank 2013). Time
applications are often bilateral, so T = 2. Successive
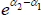 are then
combined to form a longer time series. Such is the approach behind official calculations of Australian
computer price indices (Australian Bureau of Statistics 2005).
are then
combined to form a longer time series. Such is the approach behind official calculations of Australian
computer price indices (Australian Bureau of Statistics 2005).
- The notation and format differs across applications in the literature. When T = 2 and the population is static, the format is sometimes in first differences. In levels, The Standard Model often includes a constant and the fixed effects are normalised to a base.
Note that in all applications the (t, v) pairs are restricted to have a single price. For housing markets, where each home is a unique variety, the single price feature is natural if the time periods are short enough to rule out successive sales. For most other markets it is unnatural and national statistical offices use unit values to resolve the multiple prices problem. Section 4.3 will discuss the use of unit values. For now the reader can ignore them.
It is often unclear whether other applications of The Standard Model really do assume strict error exogeneity. Theoretical work on the equilibria of differentiated product markets, such as Rosen (1974), Berry, Levinsohn and Pakes (1995), and Pakes (2003), suggests that for the general case the assumption is too strong. Unless specv is empty and the Model consists only of αt, the true conditional expectation for price need not take the proposed linear form (see Hansen (2018, ch 2)). For the hedonic case of The Standard Model, the same point is emphasised in Triplett (2004) and Brachinger, Beer and Schöni (2018).
The strength of the strict exogeneity assumption is also unnecessary. For instance, according to Diewert (2005, p 775), ‘the price statistician takes a descriptive statistics perspective’. To effect a descriptive statistics perspective in this modelling set-up requires only that the population errors are uncorrelated with the implied regressors. In the more formal econometric language of, for instance, Solon, Haider and Wooldridge (2015, p 303), a ‘projection’ is sufficient.
I make the strict exogeneity assumption because weaker versions of it will only turn out to strengthen my conclusions. It simplifies explanations as well. Later I will relax it.
2.2 The Literature Favours Weighted Estimators
After collecting, say, a large random sample of varieties, practitioners must decide how to estimate the αt.
Without more information, standard econometric practice would be to use ordinary least squares (OLS). Indeed, OLS was used for the equivalent of a static population, T = 2 set-up as early as Jevons (1869). In that case OLS produces what is now called a Jevons price index, i.e.
where V is the total number of unique varieties in the sample. Each price ratio (or ‘price relative’) is given equal weight in calculating the overall price change between periods 1 and 2.
But when quantities data are also available, influential scholars have argued against using equally weighted measures of price change for most measurement applications.
Everyone knows that pork is more important than coffee and wheat than quinine. Thus the quest for fairness lead to the introduction of weighting. (Fisher 1922, p 43)
Thus if price relatives are different, then an appropriate definition of average price change cannot be determined independently of the economic importance of the corresponding goods. (Diewert (2010, p 252) paraphrasing Keynes (1930))
… we should use a weighted regression approach, since we are interested in an estimate of a weighted average of the pure-price change, rather than just an unweighted average over all possible models, no matter how peculiar or rare. (Griliches 1971, p 8)
These views have been influential. Heravi and Silver (2007, p 251) even take weighting as ‘axiomatic’. To implement weighting, the dominant preference now is to estimate the αt with weighted least squares (WLS), using weights for economic importance. Works that support or use weighted estimation for special cases of The Standard Model include measurement handbooks from International Labour Office et al (2004) and International Labour Organization et al (2004), an econometric textbook by Berndt (1991), various statistical agency series, and countless research publications, including from recent years.
The preferred weights typically relate to expenditure shares. In a static T = 2 set-up they might look like
where qtv is for transaction quantities and the stv are expenditure shares. Estimation then produces an index number advocated by Törnqvist (1936), i.e.
(Derivations of Equations (3) and (5) are in Diewert (2005).)
The Törnqvist index is common in research applications and at national statistical offices. It is, for example, being used for an official chained measure of US consumer prices (Bureau of Labor Statistics 2018). Assessments using the so-called economic approach to index numbers shows it to have excellent properties (Diewert 1976). Judging by Clements et al (2006), the properties have further promoted WLS in other applications of The Standard Model.
The handbooks from International Labour Office et al (2004, p 301) and International Labour Organization et al (2004, p 420) also discuss an option of weighting implicitly, whereby the probability of sampling each variety reflects its economic importance. The option is equivalent to explicit weighting.
Either way, weighting for economic importance departs from mainstream econometric practices. For example, it is absent from a list of econometric justifications for weighting in Solon et al (2015), which is somewhat of a weighting handbook. Diewert (2005) also emphasises this ongoing tension between standard measurement and econometric considerations.
Occasionally the stated econometric justification for the weights is that error variance is lower for varieties with higher economic importance. For instance, Clements and Izan (1981) argue that national statistical offices might invest more resources in making accurate price measurements of varieties that command more spending. A pursuit of econometric efficiency could then justify weighting. Clements and Izan (1987) later use data on Australian consumer prices to reject the error variance hypothesis in that case.
Triplett (2004) offers another perspective, drawing on a well-known property of WLS. With exogenous weights and assumptions A1 to A4 satisfied, WLS is consistent and unbiased, just like OLS. Even if WLS is less efficient, in large samples the difference is negligible.
2.3 The Weighted Estimators are Inconsistent
Typically omitted from the conversation is that the weights are in fact endogenous. Expenditure shares contain prices, which are functions of the errors. They also contain quantities, which can be functions of the errors via prices. Either way, WLS is inconsistent because it over-represents observations with errors of a particular sign.
The justification from Triplett (2004) breaks down because it works only for exogenous weights. Arguments based on efficiency improvements are problematic too; even when the premise about error variance is correct, the efficiency benefit from weighting would have to outweigh the cost of inconsistency.
The degree of inconsistency comes from the coefficients in a so-called weighted linear projection of the errors on the regressors. That is, using δ and xtv as vector shorthand for all the coefficients and regressors that are implied in The Standard Model,
Appendix A contains a derivation. The final expectation term is not zero because the wtv are functions of the εtv.
What then transmits into the price index is the difference in the inconsistencies of the estimated fixed effects. It can be subtle. Some stylised scenarios help to develop the intuition and to set up the eventual solution. The scenarios use small samples, so the metric for central tendency switches momentarily to the degree of bias. The intuition is transferable.
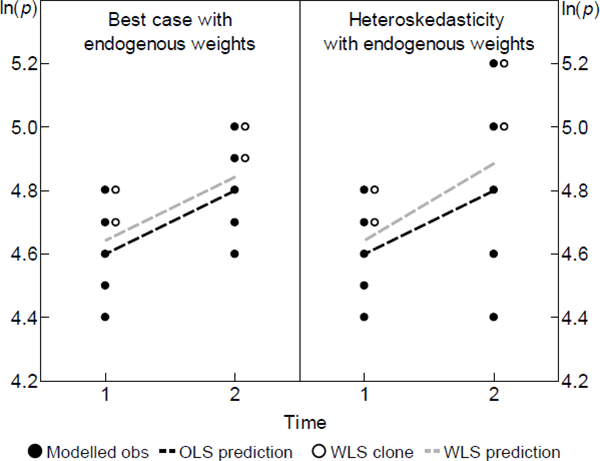
Scenarios. From a population that is static over two periods, consider a random sample of
five varieties, like the solid dots in the left panel of Figure 1. Let the
specv vector be empty, so the spread of within-period prices comes only
from the errors. In this case the strict exogeneity assumption is trivially sensible. The 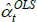 trace out a prediction
that intersects the simple arithmetic average of observed log prices in each period. The estimates are
unbiased.
trace out a prediction
that intersects the simple arithmetic average of observed log prices in each period. The estimates are
unbiased.
The left panel also introduces WLS, which is equivalent to cloning observations in numbers proportional to
their weight, before applying OLS. If in repeated samples the weights are positively related to the errors
as depicted, WLS will tend to trace out higher predictions for log prices. The 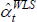 will be biased. But the key is
will be biased. But the key is 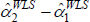 . As evident in the parallel slopes of the fitted
lines, it need not be biased. To be biased the covariance of errors and weights needs to change across the
two periods. The right panel shows that the change could arise from something so common as
heteroskedasticity.
. As evident in the parallel slopes of the fitted
lines, it need not be biased. To be biased the covariance of errors and weights needs to change across the
two periods. The right panel shows that the change could arise from something so common as
heteroskedasticity.
Some scanner data studies contain empirical comparisons of the Jevons and Törnqvist indices (Feenstra and Shapiro 2003; de Haan and van der Grient 2011; Fox and Syed 2016). Both index types are estimators for the static T = 2 version of The Standard Model, but the Törnqvist index uses endogenous weights. Since scanner data have large cross-sections, the studies can help to gauge the degree of inconsistency introduced by endogenous weighting. Fox and Syed (2016), for instance, use over 20 million observations to construct monthly price indices for basic household products, sold across six major US cities. The difference between the indices accumulates to about 12 percentage points over eleven years.
Also recall that in versions of The Standard Model for which the specv vector is non-empty, it is more realistic to assume the errors are only uncorrelated with the regressors, rather than strictly exogenous. The model parameters then describe a linear projection, not a conditional expectation. Weighting in the projection case – even if the weights are exogenous – can concentrate estimation on domains that consistently produce quite different linear projections. Hence the potential for inconsistency grows. Appendix B explains formally.
Previous mentions of the endogenous weighting issue are sparse and brief. One mention appears in Feenstra (1995), who switches immediately to using exogenous weights. Another appears in Clements et al (2006), who then point to an alternative model. Two appear in Diewert (2010), who then questions the stochastic approach to index numbers. de Haan (2004) points out that endogenous weights might be problematic in a footnote. Persons (1928) also describes the issue, although not using a stochastic framework. There being no systematic objection in the literature, endogenous WLS has remained the norm.
2.4 We Have Just Been Using the Wrong Model
The temptation here is to argue again for OLS, or maybe to seek out an instrument for expenditure shares. But the weighted estimators carefully incorporate the viewpoint of Keynes and Fisher. The problem is that the parameters of interest, as defined by the assumptions of The Standard Model, do not.
In particular, the parameters trace out the population conditional expectation of log prices. In turn, the conditional expectation operator is ignorant of the revenue profiles of each variety, putting equal emphasis on transaction prices that occur with equal probability. The macro viewpoint of Keynes and Fisher is deliberately unequal in its emphasis though. The emphasis it puts on prices depends on the expenditures that the corresponding varieties command in the market.
Although not intended to resolve the inconsistency, a more appropriate model specification has actually come up before, in Diewert (2005). An equivalent form also appears in Diewert, Heravi and Silver (2009). Its key innovation is to restate The Standard Model in units that do deserve equal emphasis. That is, if one variety has twice the economic importance of others, the model counts it as two identical varieties.
Figure 2 depicts the change informally. It reproduces the scenario in the right panel of Figure 1, now from the viewpoint of the restated model. What before were just estimator clones have become modelled observations in their own right. In other words, some (t, v) pairs are modelled to contain many of what I call units of ‘equal interest’.
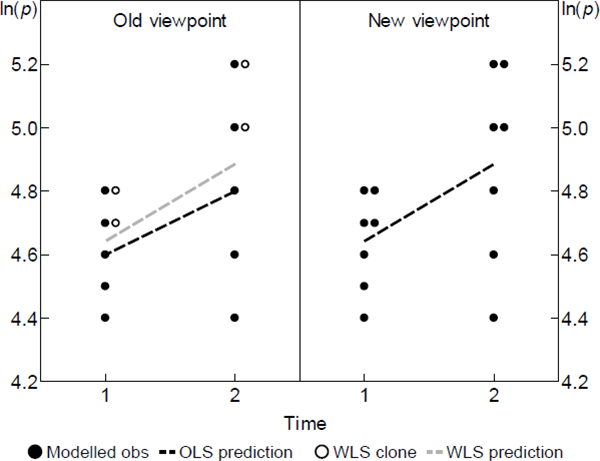
Although I have loosened some assumptions, the formal representation of the model swaps A1 and A3 with A1′ and A3′. Call this The Diewert Model.
A1′
where the new subscript u is for unit of equal interest. The total number of units in each (t, v) pair, Utv, is proportional to the preferred weight (proportionality, rather than equality, is needed to handle the non-integer weights). The other notation is unchanged, although note that αt and β will take on different values than the corresponding case of The Standard Model. I have retained the same notation to avoid a proliferation of terms. Future values of αt and β will be different again.
A3′ The errors are uncorrelated with the implied regressors.
In A1′, the new u subscript is not introducing another dimension of variation (yet), although its ability to introduce another dimension will be an advantage. Its role, for now, is to emphasise that some (t, v) pairs matter more for the identification condition in A3′ than other pairs do. It would be more natural to disaggregate into varieties, or transactions, but respecting the macro viewpoint of Keynes and Fisher calls for a population of interest with a synthetic disaggregation.
In A3′ the switch to uncorrelated errors is for realism. In Diewert's original formulation the errors were assumed to be strictly exogenous and homoskedastic. The choices reflect that the background econometric justification for the model was still an efficiency-based one.
The Standard Model is a special case of The Diewert Model, where all of the Utv are equal. For micro-oriented questions, this setting will still be appropriate. The decision can be a subtle one. For example, questions about the average price of dwellings (separate residences) call for micro models that give varieties equal emphasis, noting that each dwelling is a separate variety. Questions about the average price of housing (the infrastructure providing shelter) call for macro models with an unequal emphasis on varieties.
The Diewert Model, which is still uncommon in the literature, will be the main building block for the key results in this paper.
2.5 The Literature Contains Other Related Contributions
Although for brevity I am naming the model after Diewert (2005), the literature contains several related contributions.
Theil (1967) provides a derivation of the Törnqvist index using an original set-up. Although he does not write down a model, the expenditure weights that end up in the index do seem to come from his notion of the population of interest. The method relies on price ratios, so it does not generalise easily to multilateral comparisons and dynamic populations like The Diewert Model does. A substantial generalisation of Theil's method does appear in Diewert (2004), but the result is more cumbersome, less intuitive, and still less flexible than The Diewert Model described here.
Clements et al (2006) do write down a model, which originally comes from Voltaire and Stack (1980). It is the first to identify the right parameters, but cannot handle dynamic populations. It also lacks intuitive appeal. Appendix C elaborates on these claims.
An important and overlooked contribution has been made in an econometrics-focused paper from Machado and Santos Silva (2006). Except for its emphasis on quantity weighting (rather than expenditure weighting), the paper contains the most complete narrative on the econometric justification for measurement weights. The authors write that if the parameters of interest come from a model for prices of individual transactions, a random sample of varieties is actually endogenous. OLS is inconsistent. They further explain that WLS, with weights for transaction quantities, can unwind the inconsistency. Their insight reveals that we should view the weights in measurement estimators as corrections for endogenous sampling. This is a more conventional econometric justification for weighting, which does appear in the handbook-type article of Solon et al (2015). There should be no perceived tension between econometrics and measurement.
In some other papers the relevance of a contribution is unclear, especially where there is a tendency to blend the concepts of models and estimators.