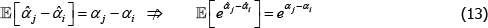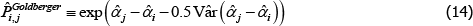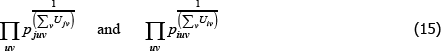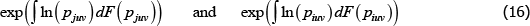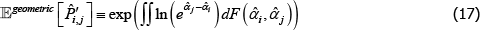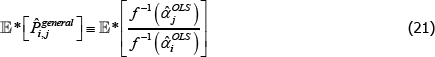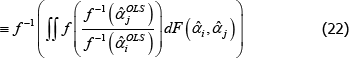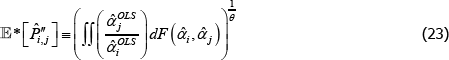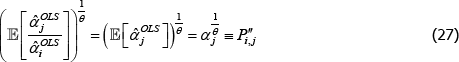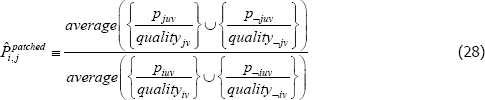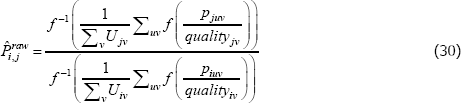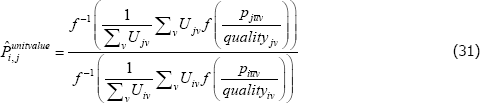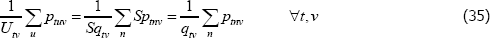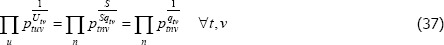RDP 2018-08: Econometric Perspectives on Economic Measurement 4. The New Framework Challenges Some Practices
July 2018
- Download the Paper 1,726KB
4.1 The Goldberger (1968) Bias Correction is Unnecessary
For models with a semi-log form, like The Standard Model, the international consumer and producer price index manuals recommend a bias correction for 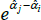 (International Labour Office et al 2004, p 118; International Labour Organization et al 2004, p 184). Following Goldberger (1968), the correction is to account for the fact that
(International Labour Office et al 2004, p 118; International Labour Organization et al 2004, p 184). Following Goldberger (1968), the correction is to account for the fact that
The Diewert Model is also semi-log, so the same applies. The proposed bias-corrected estimator is
where Vâr (·) is estimated variance. The correction matters most when the variance of 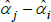 is largest, which, in turn, is more likely for cases with small sample sizes and few controls. An empirical illustration in Kennedy (1981) shows the correction to make a small difference. More measurement-focused illustrations in Syed, Hill and Melser (2008) and de Haan (2017), show it to make a trivial difference. However, these examples use large samples and many controls. As pointed out by Hill (2011), we cannot rule out there being cases for which the correction is material.
is largest, which, in turn, is more likely for cases with small sample sizes and few controls. An empirical illustration in Kennedy (1981) shows the correction to make a small difference. More measurement-focused illustrations in Syed, Hill and Melser (2008) and de Haan (2017), show it to make a trivial difference. However, these examples use large samples and many controls. As pointed out by Hill (2011), we cannot rule out there being cases for which the correction is material.
But even in cases where the bias correction matters, is it sensible? Here I show that it seems to imply incompatible analytical preferences.
With the αt coming from a semi-log model, defining the measurement objective as 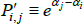 is just articulating that the preferred measure of central tendency is a geometric average. In particular, taking a finite view of the population, which is a common choice in the measurement literature, revealed preference is for a ratio comparison of
is just articulating that the preferred measure of central tendency is a geometric average. In particular, taking a finite view of the population, which is a common choice in the measurement literature, revealed preference is for a ratio comparison of
For a more standard, continuous view of the population, the corresponding geometric-type averages look more complicated. They are
where F(·) is a cumulative density function and the integrals are over u and v.
If interest is in geometric-type averages like these, why then would we subject 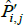 to a standard test of unbiasedness, which is an arithmetic criteria of central tendency? Logical consistency would dictate the use of a compatible, geometric criteria.
to a standard test of unbiasedness, which is an arithmetic criteria of central tendency? Logical consistency would dictate the use of a compatible, geometric criteria.
It turns out that with a geometric criteria a correction is unnecessary. In particular,
where 𝔼geometric [·] is a geometric type of expectation operator and F(·,·) is a cumulative density function.
The natural follow-up question is whether compatible criteria of central tendency always generate such benign results. The answer: not necessarily.
To illustrate, let 𝔼* denote an expectation operator that is logically consistent with the choice of f (·), such that
Now let f (x) = xθ, where θ is a non-zero real number. Along with f (x) = x, this setting for f (x) covers all of those that currently appear in the measurement literature. Denote the corresponding index and target as 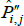 and
and 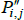 . Generally it will be the case that
. Generally it will be the case that
There are, however, important special cases. In particular, many indices use definitions of quality for which qualitytv = priceiuv for all t, u, and v. In that case it always holds that 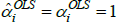 =1. Hence
=1. Hence
This is an unusual result. It means that for indices like Paasche, interpretations that set qualitytv = priceiuv are more achievable in small samples than other interpretations.
4.2 Some Dynamic Population Methods Look Questionable
In durable goods markets especially, the norm is for the population of transacted varieties to be dynamic. Yet index functions, the primary tools of economic measurement, are designed for static populations of varieties.
A crude workaround is to drop orphan varieties. However, the prevailing view in the field of measurement is that orphan status is non-random. Dropping the orphans generates what is akin to another endogenous sampling problem. More sophisticated methods are needed. According to Triplett (2004, p 9), handling quality change that comes from a changing population has ‘long been recognised as perhaps the most serious measurement problem in estimating price indexes’. Moulton (2017) explains how successive investigations have estimated that the problem accounts for the largest source of measurement bias in the US consumer price index.
The updated stochastic approach presented here offers a useful perspective on the problem. As shown below, without any intrinsic dependence on price ratios, it provides avenues through which to extend index function principles to dynamic populations. It is also a means to identify existing dynamic population methods that are incompatible with the (stochastic approach) principles behind index functions.
When extending to dynamic populations, not all of the features of index functions can be preserved, and compromises are necessary:
-
Some choices of {qualitytv} become undefined. In particular, {qualitytv} cannot be benchmarked to prices if some of them are missing from the population. In this case, the missing transaction prices that are needed to fully define {qualitytv} might defensibly be viewed as having synthetic values, each corresponding to what might have been the price had the variety been transacted.
In the estimation phase, coming up with these values is often called ‘patching’ or ‘imputing’. The measurement literature already contains many approaches to patching (see International Labour Office et al (2004), International Labour Organization et al (2004), and Eurostat (2013)).
- Section 3.2 showed that, in static populations, some distinct combinations of f (x), {Utv}, and {qualitytv} coincide with others. The same feature breaks down in dynamic populations. So practitioners looking to generalise an index function to a dynamic population must choose just one combination. Alternatively, they could choose several combinations, calculate a separate index for each, and take an average. The latter approach is similar in spirit to, say, the ideal index from Fisher (1922).
Strategies like these are already being used. For instance, when constructing an index directly from a dynamic population version of The Standard Model, practitioners are implicitly choosing a single definition for {qualitytv}, based on a least squares criteria. Using the method of moments approach outlined in Rao and Hajargasht (2016) (examples are in Appendix F), a least squares criteria for choosing {qualitytv} could be executed under all sorts of other settings for f (x) and {Utv}.
The literature contains criticisms of this direct method, which have stifled take-up by national statistical offices. The key criticism is ultimately about the definition of quality. For instance, in 2002, responding to a request by the US Bureau of Labor Statistics (BLS), a panel of experts wrote:
Recommendation 4-4: BLS should not allocate resources to the direct … method (unless work on other hedonic methods generates empirical evidence that characteristic parameter stability exists for some products). (National Research Council 2002, p 143)
The concern is that restricting the coefficients on variety specifications to be fixed over time is unlikely to reflect the true conditional expectation function for prices. Several papers have rejected parameter stability for the computer market in the United States (Berndt and Rappaport 2001; Pakes 2003), and have echoed the panel's recommendation (see also Diewert et al (2009) and Hill (2011)).
Viewed through the updated stochastic approach, this argument looks problematic for two reasons:
- The objection really is to fixing the quality definition across t, within varieties. Yet the same is true of all common index numbers. If fixing each variety's quality definition is indeed a drawback, index function choices need to be reconsidered too. Functions with quality definitions that change over t, like the common goods index from Redding and Weinstein (2018), would need to become more mainstream.
- To repeat a point made already, there is no need for the model to describe the conditional expectation function exactly (i.e. requiring the errors to be strictly exogenous to the regressors). It is sufficient for the model to identify useful descriptive statistics (i.e. accepting errors that are only uncorrelated with the regressors).
Moreover, the proposed alternatives do not actually address the fixed quality problem. For instance, the most popular alternative is to use synthetic values for all missing transaction prices, not just the missing prices needed to define quality. Standard index functions can then be applied. However, no matter where those synthetic values come from, the index functions that are typically applied to the new population still take constant quality perspectives. Moreover, the interpretation of the final index is no longer an average of quality-adjusted actual prices. Instead it is
where the ¬juv indexes fictitious product observations, from the additional patching. The same issue transfers to the population target. (Conditions under which the additional patching makes no difference are provided in de Haan (2008).)
Diewert et al (2009) examine and propose another alternative, which they show is also equivalent to the so-called characteristics prices method. The method is fully consistent with the new stochastic approach presented in this paper, it being akin to calculating indices for several combinations of f (x), {Utv}, and {qualitytv}, before taking an average. Still, the underlying quality definitions are fixed over time.
Note that Feenstra (1994), Ueda, Watanabe and Watanabe (2016), and Redding and Weinstein (2018) introduce other, deterministic methods to handle dynamic populations. The methods do not seem to have obvious connections to the stochastic approach presented here, but are justified by the economic approach.
Occasionally, the literature also defines dynamic population indices using models that are like The Standard Model, except that the dependent price variable is in levels, rather than logs. Since this set-up is obviously not a special case of Equation (8), it is also in conflict with the principles behind the stochastic approach.
4.3 Unit Values Can Distort Index Number Interpretation
So far we have assumed that each (t, v) pair has a single price. The assumption is unrealistic in the general case, even with fully efficient markets. For instance, each t is an area, not a point, in space or time. A price shock can fall easily within its boundaries. How should measurement methods handle breaches of the single price assumption?
Current practice, stemming from Walsh (1901), Fisher (1922) and Davies (1932), is to specify measurement tools in terms of ‘unit values’ (see International Labour Office et al (2004) and International Labour Organization et al (2004)). Regardless of the situation, the unit values are always equal to the total measured expenditure on each (t, v) pair, divided by the number of units transacted. That is, letting 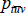 denote the unit value for pair (t, v),
denote the unit value for pair (t, v),
where the subscript n tracks each of the individual transactions. Unit values are hence quantity-weighted, arithmetic averages of prices.
The attraction of the unit values solution is that it can shoehorn reality into the traditional formulation of index functions. Moreover, it has low information requirements, needing only total expenditures (numerator) and numbers of transactions (denominator) for each variety. But the functions – and their population targets – are then comparing averages of quality-adjusted unit values at different points in space or time. Are there sensible ways to preserve a cleaner interpretation, about quality-adjusted raw prices? Would the outcomes even be different?
With its more flexible formulation, the new stochastic approach framework presented in this paper is an avenue through which to tackle these questions. Diewert (2004) and Rao and Hajargasht (2016) also noted the potential of stochastic approaches to handle raw prices if they are available.
Preserving the raw prices interpretation requires only that, for each variety in a given time period, the units of equal interest are allocated to the different transaction prices somehow. Since each of the transactions for a variety are (definitionally) for a homogeneous product, it seems the only sensible solution is to allocate units of equal interest in proportion to the number of transactions executed at each price. Sometimes this will correspond to the unit values solution, but sometimes it will not.
To illustrate, I will focus on index functions, rather than their population targets. The same ideas carry over easily though.
Denote the index that uses raw prices as
and the one that uses unit values as
The indices are equivalent if
Letting f (x) = x, a common choice for many indices, the condition reduces to
Now, use S to denote some strictly positive scalar, and allocate the units of equal interest evenly across each transaction. The raw prices calculation on the left-hand side of Equation (34) becomes
The result does indeed correspond to the unit values solution on the right-hand side of Equation (34). The unit value method looks ideal.
For other choices of f (x) the unit value method looks less benign. For instance, consider the choice of f (x) = ln(x). Equivalence to the raw prices method is guaranteed only when
If units of equal interest are allocated evenly across transactions, the raw prices solution on the left-hand side becomes
Equivalence to the unit values method is unlikely to hold, since
When there is any variation in transaction prices for a given (t, v) pair, the inequality is strict (Balk 2008, p 70).
So for some types of f (x), the unit value method necessarily changes the interpretation of the index, or can be seen as distorting the true index. This should be unsurprising; the unit value method takes a position on the appropriate measure of central tendency without considering the choice of f (x), which is also a position on the appropriate measure of central tendency.
4.4 There Are Obvious Avenues for Further Progress
In establishing the new stochastic framework, and the results that come from it, this paper has left many obvious questions unanswered:
- Can we determine exactly how many distinct combinations of f (x), {Utv}, and {qualitytv} correspond to each price index? And can we be precise about what those are? The answers would be useful for comparing the merits of various functions. They might also yield new options for handling dynamic populations.
- Can we definitively rule out some indices from complying with the stated paradigm? If so, is this a problem with the paradigm or the index?
- What corrections are sensible for the measurement approaches that have undesirable central tendencies in small samples? Would the corrections ever be material enough to promote for use at national statistical offices?
- How material in practice are the unit value distortions that I have identified?
- What does the new framework imply for appropriate confidence intervals? Do the implications align with existing work on index number uncertainty, such as Crompton (2000), Clements et al (2006), and Rao and Hajargasht (2016)?
- Should the same perspectives on the population of interest be incorporated elsewhere in the empirical macro literature?
These are potentially fruitful subjects for future work. The final one is the topic of a forthcoming paper. With time, the deeper connections to the econometric literature might reveal other opportunities.