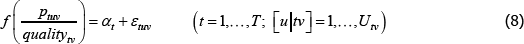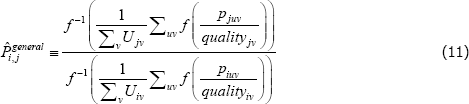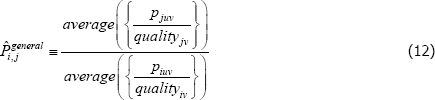RDP 2018-08: Econometric Perspectives on Economic Measurement 3. Index Numbers Share Econometric Foundations
July 2018
- Download the Paper 1,726KB
3.1 The Diewert Model Generalises Further
Using The Diewert Model, and equipped with a random sample of units of equal interest (i.e. sampling based on economic importance), the preferred measure of price change between two specific t (i and j) is Pij = exp 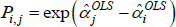 . A more general version of the same approach will turn out to be useful. It starts with a population model defined by the trivially achievable assumptions A1* to A3*.
. A more general version of the same approach will turn out to be useful. It starts with a population model defined by the trivially achievable assumptions A1* to A3*.
A1*
such that: f (·) is a strictly monotonic function; ptuv, αt, εtuv, Utv are understood already; and qualitytv is some strictly positive scalar used to standardise the price of variety v at time or territory t. Remember the αt need not take the same values as in the previous models. Moreover, the αt can change with, say, different choices of f (·) (more on this below).
A2* Across varieties the observations are independently and identically distributed.
A3* The errors are uncorrelated with the implied regressors. Note that the implied regressors are now just dummies for t, which means that strict error exogeneity is also satisfied, for free. Moving quality to the left-hand side also allows it to be defined more loosely than was exp(β′specv).
Interest then lies in the quality-adjusted price index
The corresponding index measure becomes
And since the 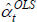 will just be arithmetic sample averages,
will just be arithmetic sample averages,
Equation (11) is a ratio of what in the mathematics literature are called Kolmogorov or quasi-arithmetic means (see Fodor and Roubens (1995)). The role of f (·) is to pin down the specific type of mean, or average. A more intuitive form for the index is thus
The average operator might be, for instance, the arithmetic mean (equivalent to f (x) = x), the geometric mean (f (x) = ln(x)), or the harmonic mean (f (x) = x − 1). Although in a cosmetically different format, the same generalised approach to averaging actually appears in recent measurement work by Brachinger et al (2018).
The specific cases of 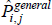 , and the target index
, and the target index 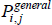 , are differentiated by distinct choices for the type average (f (·)), what merits equal interest ({Utv}), and what defines the quality of varieties ({qualitytv}). Stress is on distinct because some choices are always equivalent:
, are differentiated by distinct choices for the type average (f (·)), what merits equal interest ({Utv}), and what defines the quality of varieties ({qualitytv}). Stress is on distinct because some choices are always equivalent:
- Choosing any function f (·) is equivalent to choosing any of its affine transformations A + B(f (·)).
- Any transformations of {Utv} that preserve the relative emphasis on varieties within t do not matter. So choosing any {Uiv, Ujv} is equivalent to choosing transformations of the type {CUiv, DUjv}, where C and D are strictly positive scalars.
- For f (x) = ln(x) and all f (x) = xθ, where θ is a non-zero real number, choosing any {qualitytv} is equivalent to choosing any of its linear transformations {Hqualitytv}, where H is a strictly positive real number.
Appendix D substantiates the first two claims. The third comes from a linear homogeneity result originally established by Nagumo (1930).
3.2 Three Choices Distinguish Price Index Functions
The literature contains hundreds of different bilateral and multilateral price index functions. Most, if not all, are recorded or referenced across publications by Fisher (1922), Sato (1974), Banerjee (1983), Bryan and Cecchetti (1994), Hill (1997), Balk (2008), von Auer (2014), Rao and Hajargasht (2016), Gábor-Tóth and Vermeulen (2017) and Redding and Weinstein (2018). Some come from intuition and experimentation, and some from derivations using the economic approach. Yet it turns out – and this is the central contribution of the paper – that the simple identity in Equation (12) describes practically all of them.
More precisely, the identity in (12) describes at least all of the recorded price index functions that:
- treat t as discrete. This excludes a continuous time index from Divisia (1926).
- are explicit. This excludes types that are defined uniquely as the residual of a quantity index. The most prominent example is the so-called implicit Törnqvist price index, discussed in Diewert (1992).
- are not the esoteric bilateral types that were proposed in work by Montgomery (1937), Stuvel (1957), and Banerjee (1983), or early multilateral types that were excluded from a taxonomy of multilateral indices in Hill (1997). (Balk (2008, p 35) provides the references for these multilateral exceptions, starting with Theil (1960) and Kloek and de Wit (1961)).
This result is related to the main contribution of a paper by de Haan and Krsinich (forthcoming), which is to show that some seemingly quite different bilateral functions can be understood as averaging quality-adjusted prices. Their finding is nested in the generalisation here. Also note that, with time, the carve outs listed above could still turn out to comply with the paradigm. They are not yet proven exceptions.
Table 1 lists some of the complying bilateral functions and their settings for f (x), {Utv}, and {qualitytv}. Emphasis is on types that are most important to measurement practitioners, based on my judgement and the results of a statistical agency survey in Stoevska (2008). The table also lists some for their unusual forms. It omits types that are averages of others, such as a celebrated ‘ideal’ function from Fisher (1922, p 142 Formula 153).
| Index name (year) | f (x) | qualitytv | Utv | |
|---|---|---|---|---|
| Dutot (1738) | x | zv ∈ℝ++ | qualitytv | |
| Carli (1764) | x | p1v | 1 | |
| ⋮ | ⋮ | x − 1 | p2v | 1 |
| Jevons (1863) | ln(x) | zv ∈ℝ++ | 1 | |
| Coggeshall (1886) | x − 1 | p1v | 1 | |
| ⋮ | ⋮ | x | p2v | 1 |
| Laspeyres (1871) | x | zv ∈ℝ++ | qualitytvq1v | |
| ⋮ | ⋮ | x | p2v | qualitytvqtv |
| ⋮ | ⋮ | x − 1 | p1v | p2vq1v |
| Paasche (1874) | x | zv ∈ℝ++ | qualitytvq2v | |
| ⋮ | ⋮ | x | p1v | qualitytvqtv |
| ⋮ | ⋮ | x − 1 | p2v | p1vq2v |
| Walsh (1901, type a) | x | zv ∈ℝ++ | ||
| Fisher (1922, Formula 33) | x | p1v | ∈(0,1) | |
| ⋮ | ⋮ | x − 1 | p2v | ∈(0,1) |
| Törnqvist (1936) | ln(x) | zv ∈ℝ++ | 0.5(s1v + s2v) | |
| Lloyd (1975)–Moulton (1996) | x1 − σ | p1v | qualitytvq1v | |
| Sato (1976)–Vartia (1976) | ln(x) | zv ∈ℝ++ | ||
| Redding and Weinstein (2018) | ln(x) | 1 | ||
| ⋮ | ⋮ | ln(x) | ψv | |
|
Notes: The Dutot, Carli, Laspeyres, Paasche and Moulton attributions have all been taken on authority of Balk (2008); zv ∈ℝ++ is intended to mean that any strictly positive definitions of quality that are fixed across t, are admissible; is a weighted median of the items in set {xv}, using weights of yv (the notation is non-standard); the notation ∈(0,1) reflects that in median- and mode-based functions, only one observation has a non-zero weight; ; σ is a consumer elasticity of substitution; the index from Redding and Weinstein (2018) is what the authors refer to as the ‘common goods’ index; ψtv is a time-varying preference parameter, explained further in the original paper |
||||
Notice that many types correspond to several distinct combinations of f (x), {Utv}, and {qualitytv}. To exhaustively list the combinations associated with each type is a difficult problem, left for future work. The result of that work might be surprising. To illustrate, Appendix E includes a derivation from Bert Balk (pers comm, 16 March 2018) that generates an unexpected combination for the Dutot function. Knowing all of the combinations would help for comparing the merits of the functions, because it would demonstrate the breadth of relevant measurement preferences for which each function is exact.
Still, it is clear that at least some types cover every possible {qualitytv} that is fixed over t. This quality-robust feature adds to their appeal. Otherwise the functions tend to gauge qualitytv through relative prices. To gauge qualitytv like this is an objective choice.[1]
A notable exception for the way it gauges qualitytv is a static-population function from Redding and Weinstein (2018). It uses expenditure shares and allows qualitytv to vary over t. Derived using the economic approach, the function aims to measure cost of living changes under dynamic preferences. Using expenditure to gauge product quality like this has strong parallels in the international trade literature. (Notable examples are papers by Khandelwal (2010) and Feenstra and Romalis (2014)).
Work by von Auer (2014) outlines a so-called Generalised Unit Value Index Family, which is relevant here as well. Using the framework of this paper, the Family members are functions for which f (x) = x, {qualitytv} is fixed over t within varieties, and Utv = qualitytvqtv for all (t, v) pairs. (von Auer introduced axioms for sensible quality definitions as well.) Examples in the table are the indices of Paasche and Laspeyres. The Family is special because the implied quantity index is always the growth in the number of units of equal interest, which, in turn, are just the amounts of transacted quality. This is an intuitive, appealing feature, and one way to interpret official measures of output growth in, for instance, Australia and the United Kingdom.
The literature on multilateral functions is more niche. Table 2 lists examples of some of the types, from different parts of the taxonomy in Hill (1997). Rao and Hajargasht (2016) summarise how several of them are used to calculate official purchasing power parity statistics from the World Bank. The table does the measures a disservice because there is a lot of ingenuity behind qualitytv definitions that I have had to abbreviate to  , and
, and 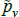 . Actually, while not the intention of the developing authors, those quality definitions all correspond to efficient method of moments estimates. This result is an adaptation of insights from work by Rao and Hajargasht (2016) (adapted because our stochastic approaches are different). Only the
. Actually, while not the intention of the developing authors, those quality definitions all correspond to efficient method of moments estimates. This result is an adaptation of insights from work by Rao and Hajargasht (2016) (adapted because our stochastic approaches are different). Only the 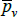 result, relating to the Geary-Khamis index, is new. Details are in Appendix F.
result, relating to the Geary-Khamis index, is new. Details are in Appendix F.
| Index name (year) | f (x) | qualitytv | Utv | |
|---|---|---|---|---|
| Walsh (1901, type b) | ln(x) | zv ∈ℝ++ | ||
| Walsh (1901)–Van Ijzeren (1956) | x | zv ∈ℝ++ | ||
| ⋮ | ⋮ | x − 1 | piv | |
| Geary (1958)–Khamis (1972) | x | qualitytvqtv | ||
| ⋮ | ⋮ | x − 1 | ptvqtv | |
| Rao (1990) | ln(x) | stv | ||
| Hajargasht and Rao (2010, type a) | x | stv | ||
|
Notes: zv ∈ℝ++ is intended to mean that any strictly positive definitions of quality that are fixed across t, are admissible; the Van Ijzeren attribution is taken on authority of Balk (2008); precise definitions of are available in Appendix F; see Hill (1997) for details on |
||||
3.3 This Changes the Stochastic Approach
Throughout this paper, measurement objectives have been defined using parameters from econometric models. Econometric estimators have then justified the corresponding measurement tools. When the population of varieties being transacted is static, the process is synonymous with the stochastic approach to choosing index functions.
To date the stochastic approach has been less influential than the economic and test approaches. It is actually more commonly used as an econometric gateway for generalising Jevons- and Törnqvist-type functions to dynamic populations. Hence the widespread popularity of The Standard Model. The approach has also been used as a means to calculate confidence intervals, to gauge index reliability (see, for instance, Rao and Hajargasht (2016)).
Judging by Clements et al (2006), the lack of influence comes partly from reservations about the stated econometric justifications for weighting. The occasional discomfort over weight endogeneity has also mattered somewhat. Section 2 has shown that both objections are fair, but resolvable. The econometric model just needs to define the parameters of interest carefully.
The new framework presented here has extended the approach in other ways as well:
- The approach now has a wider scope. It covers practically all existing price index functions and infinitely more. So it is a more complete tool for comparing them. A repercussion is that index types formerly considered as stochastic-compatible are no longer special for that reason.
- Albeit not always in a unique way, the approach now distinguishes index types by their conceptual characteristics. Previously the approach distinguished types by somewhat arbitrary modelling assumptions.
- Being specified in terms of prices, rather than price ratios, there is no built-in need for static populations that produce matched price pairs. The approach is hence a means to carry standard index function perspectives over into dynamic populations. (Some compromises are necessary, and will be discussed further in Section 4.2.)
The changes, in turn, provide an alternative means of understanding and communicating measurement challenges to economic researchers that do not have specialist backgrounds in measurement. Consider the phenomenon of chain drift, which occurs in index functions that provide different results under chained comparisons than under direct ones (see Ivancic, Diewert and Fox (2011)). The chained and direct indices imply different populations of interest, because they have different units of equal interest. Using either set-up as the correct benchmark, the gap between them can be viewed as reflecting endogeneity.
In some cases, the changes can also open new avenues for tackling measurement problems. The next section discusses three examples, and some obvious avenues for further progress. As the discussion is targeted at measurement specialists, applied macro researchers can skip comfortably to the conclusion.
Footnote
For another application the 2008 System of National Accounts does list some relevant cases in which gauging quality like this is not ideal (European Commission et al 2009, p 303). [1]