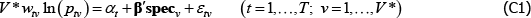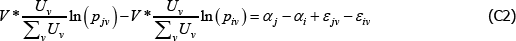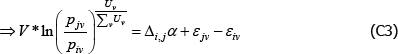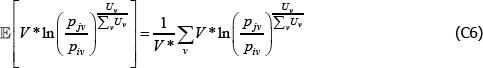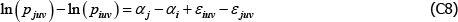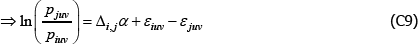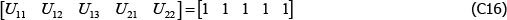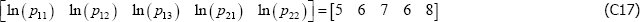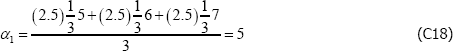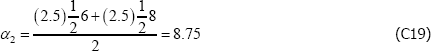RDP 2018-08: Econometric Perspectives on Economic Measurement Appendix C: The Model of Voltaire and Stack (1980) Equates to The Diewert Model, under Restrictive Conditions Only
July 2018
- Download the Paper 1,726KB
Using my notation and making some trivial generalisations, the model of Voltaire and Stack (1980) swaps A1′ for A1″.
A1″
where V* is the number of varieties in a population viewed to be finite (as opposed to the more common, superpopulation viewpoint).[2]
In the original application the population is static and wjv = wiv for all i and j. If also 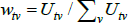 , as looks to be the intention, the model identifies the same αj – αi as the equivalent case of The Diewert Model. Otherwise the relevance of the Voltaire and Stack model is easy to break.
, as looks to be the intention, the model identifies the same αj – αi as the equivalent case of The Diewert Model. Otherwise the relevance of the Voltaire and Stack model is easy to break.
To illustrate, note that under the above conditions, for any i ≠ j, the key assumptions of the Voltaire and Stack model can be rewritten in the form
and
Therefore
Since the Voltaire and Stack model views the population as finite, with V* varieties,
Under the same conditions, The Diewert Model implies
where
Taking the same finite perspective on the population,
which mirrors the result for the Voltaire and Stack model.
However, if the population is, for instance, dynamic, the equivalence does not hold. Actually it is not even clear how to define the parameters, particularly V*. One option might be to take an arithmetic average of the variety counts in each t, but even here the model produces unusual results. To illustrate, let β′specv =0 and consider a finite population described by
The Voltaire and Stack model identifies the parameters to be
and
These are nonsensical results, particularly the second, being outside the range of population prices in t = 2. The equivalent figures for The Standard Model are α1 = 6 and α2 = 7.
The other drawback of the Voltaire and Stack model is its lack of conceptual appeal. The authors do not justify the relevance of the dependant variable, so it is unclear why the coefficients are interesting.
Footnote
The superpopulation viewpoint can encompass the finite population one, by conceptualising the population outcomes as having discrete possibilities, with densities proportional to realised incidence. [2]