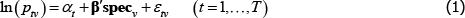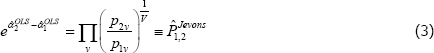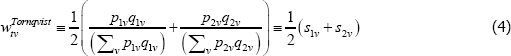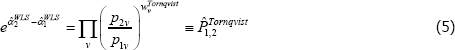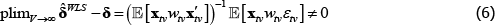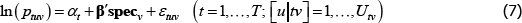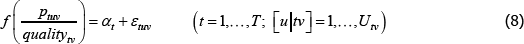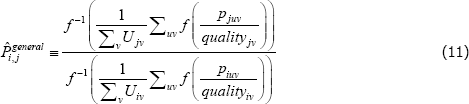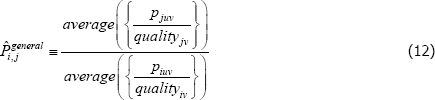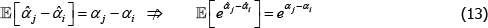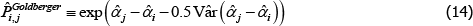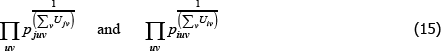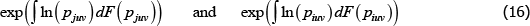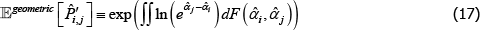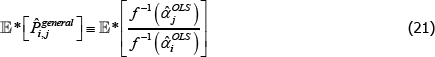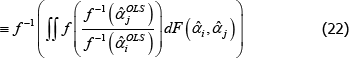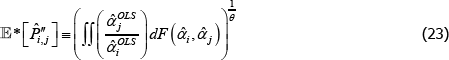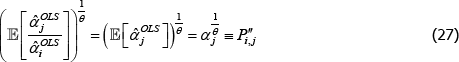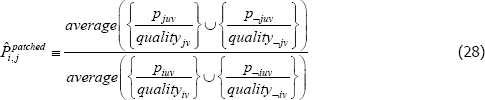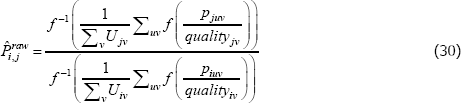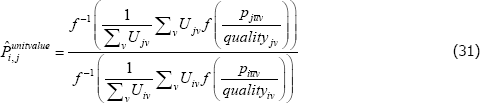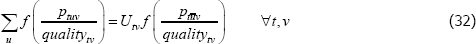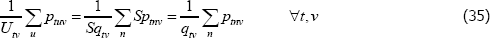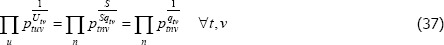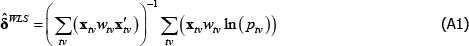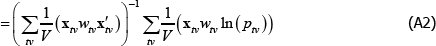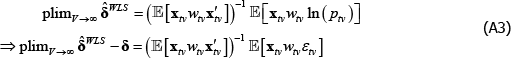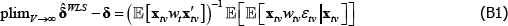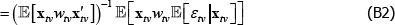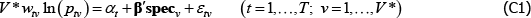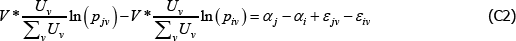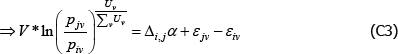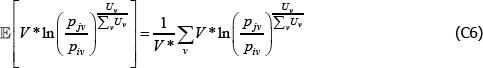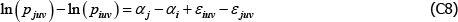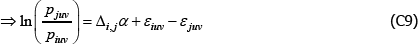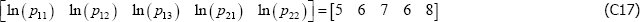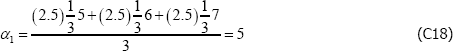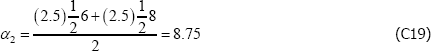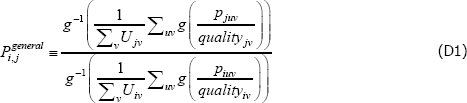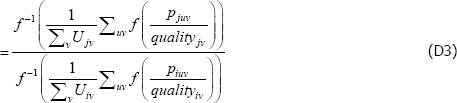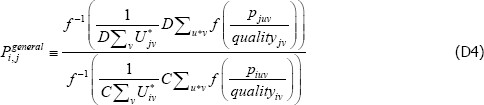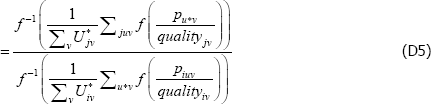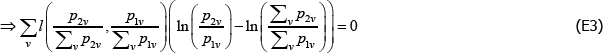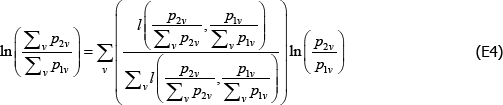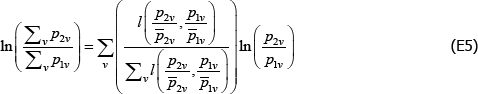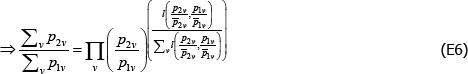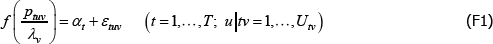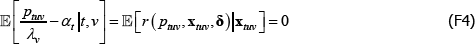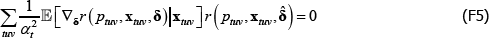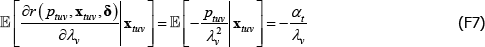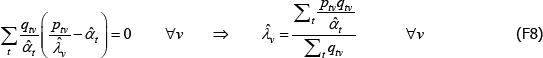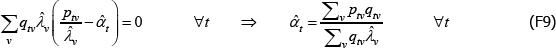Research Discussion Paper – RDP 2018-08 Econometric Perspectives on Economic Measurement
1. Introduction
All measures of macroeconomic change rely on microeconomic data. Key examples are consumer price inflation, housing price inflation, output growth, productivity growth, and purchasing power parities. Each come from micro data on market transactions, and each are cornerstones of evidence-based policy.
Yet it remains unclear how the measures should handle changes in the quality composition of the items being transacted. For instance, how should a consumer price index adjust for the improving quality of mobile phones? What even defines quality? Measurement scholars find these questions difficult. With technological advances delivering large quality improvements, sensible solutions are important. Jaimovich, Rebelo and Wong (2015) show that quality compositions can swing with business cycles as well.
When it is not the types of items being transacted that are changing – just their market shares – the primary tools for handling quality change are index functions. The literature contains hundreds of options and three main approaches for distinguishing among them:
- The ‘test’ approach (also called ‘axiomatic’ or ‘instrumental’) distinguishes functions by their ability to satisfy certain desirable mathematical properties. (Balk (2008) provides a review.)
- The ‘economic’ approach distinguishes functions by how closely they measure the changing cost of attaining a given economic objective, such as an amount of output or living standard. (Diewert (1981) provides a review.)
- The ‘stochastic’ approach distinguishes functions by how well they estimate parameters in econometric descriptions of the measurement task. (See Selvanathan and Rao (1994) and Clements, Izan and Selvanathan (2006) for reviews.) Currently the literature identifies only some functions as having stochastic justifications.
When the types of items being transacted are changing, standard index functions become undefined and alternative tools are needed. Here, extensions of the econometric methods behind the stochastic approach have been influential.
Still, this paper shows that the relevance of econometrics to economic measurement runs a lot deeper. It turns out that practically all price index functions have origins that are nested in the same econometric model. Through the model we can view the functions as comparing averages of quality-adjusted prices at different places or times. The options are distinguished by their type of average, their definition of quality, and their stance on what I label ‘equal interest’. Following normal practice, each price index implies a quantity index. What look like being exceptions to the paradigm are minor.
This result changes the stochastic approach in useful ways. First, by covering practically all bilateral and multilateral price index functions, it is more comprehensive. So the approach becomes a more complete tool for choosing among the different function types. Second, to distinguish between the types, the approach now relies on attributes that are conceptual. Previous versions of the stochastic approach have distinguished functions using modelling assumptions. The overall outcome is not a recommendation to use any specific index functions, but a logically consistent framework for differentiating and choosing among them.
In turn, the changes to the stochastic approach offer new avenues to understand and tackle measurement problems. The paper highlights three examples, by challenging: the use of a bias correction from Goldberger (1968); the widespread reliance on so-called unit values; and some common views on adjusting for quality change when the types of transacted items are changing. Sensible alternatives are sometimes immediate. With time, the deeper connections to the econometrics literature could yield others.
The new framework and the results that flow from it are the paper's main contributions. Before establishing those results though, it is necessary to do some groundwork. In particular, the next section demonstrates that econometric estimators in measurement applications are often inconsistent for the parameters of interest that are defined (or ‘identified’) by the corresponding model assumptions. Strangely, it is not the estimators that need to change, but the standard model set-up that defines the parameters of interest. These ideas overlap with other ideas that are already in the literature. By connecting and re-specifying them, it is hoped that a shift in the consensus on appropriate model specification will occur.
For the wider macro community, a side-goal of the paper is to simplify issues of measurement. Macro researchers could use the new framework to appreciate the many compromises built into macro data. The next section is therefore also intended to provide sufficient background for macro researchers without a specialist understanding of measurement.
2. The Standard Model Needs Changing
2.1 The Standard Model
The econometric model most commonly used to define the price measurement task descends from pioneering work by Court (1939). Using assumptions A1 to A4, it describes pricing behaviour in some market for differentiated product varieties. To distinguish it from a later model that will have many of the same characteristics, call it The Standard Model.
A1
where: ptv is the transaction price of variety v in time period or territory (place) t; αt is a fixed effect for t; β is a vector of parameters; and specv is a vector of observed variety specifications. Hence β′specv can be seen as a control for the effect of quality on prices. εtv is an error term.
A2 Across varieties the observations are independently and identically distributed.
A3 The errors are strictly exogenous. So
A4 Other technical conditions of regularity are satisfied, ruling out perfect multicollinearity and variables with infinite second moments.
For measurement, the interest is in the differences between the αt. For instance, if
t is for time, 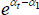 indexes a time series of the price level, holding quality constant. The series is useful for measuring inflation
and deflating nominal aggregates into real ones. If t is for territory,
indexes a time series of the price level, holding quality constant. The series is useful for measuring inflation
and deflating nominal aggregates into real ones. If t is for territory, 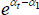 indexes a cross-section of purchasing power parities.
indexes a cross-section of purchasing power parities.
Special cases of The Standard Model shape many macro indicators. Hence, a lot of empirical macro research is linked to it somehow. Aside from variation in the concept behind t, the special cases differ along several dimensions:
- The market types vary. For instance, in official capacities The Standard Model has been applied to the rental market in the United States (Bureau of Labor Statistics 2017), the used car market in Germany (German Federal Statistical Office 2003), and the computer market in Australia (Australian Bureau of Statistics 2005). It can be applied to markets that are more broadly defined as well.
- The types of regressors in specv differ. In measurement handbooks the regressors are often variety attributes (International Labour Office et al 2004; International Labour Organization et al 2004; Eurostat 2013). In this case the model becomes ‘hedonic’. In some other cases the regressors are variety dummies and β′specv becomes a variety fixed effect (World Bank 2013).
-
The population of transacted varieties can be static, with no entry or exit, or it can be dynamic. The static case is special because t is definitionally uncorrelated with the regressors in specv. Including β′specv is thus irrelevant for defining the population price index. This is the classic setup in the prevailing stochastic approach to choosing index functions, described more fully in Section 3.3.
In measurement contexts more broadly, static populations are sometimes synthetic, in the sense that missing varieties are assumed to have hypothetical prices. Often the hypothetical prices correspond to predictions of T = 1 versions of The Standard Model (and where interest is not in the αt). This method is behind official price indices for mobile phones in the United Kingdom (Office for National Statistics 2014). Since modelling considerations then change, this paper is not about T = 1 cases, except where stated otherwise.
-
Still, the size of T can vary. Territory applications are often multilateral, so T ≥ 3,
as in versions that support official calculations of purchasing power parities (World Bank 2013). Time
applications are often bilateral, so T = 2. Successive
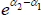 are then
combined to form a longer time series. Such is the approach behind official calculations of Australian
computer price indices (Australian Bureau of Statistics 2005).
are then
combined to form a longer time series. Such is the approach behind official calculations of Australian
computer price indices (Australian Bureau of Statistics 2005).
- The notation and format differs across applications in the literature. When T = 2 and the population is static, the format is sometimes in first differences. In levels, The Standard Model often includes a constant and the fixed effects are normalised to a base.
Note that in all applications the (t, v) pairs are restricted to have a single price. For housing markets, where each home is a unique variety, the single price feature is natural if the time periods are short enough to rule out successive sales. For most other markets it is unnatural and national statistical offices use unit values to resolve the multiple prices problem. Section 4.3 will discuss the use of unit values. For now the reader can ignore them.
It is often unclear whether other applications of The Standard Model really do assume strict error exogeneity. Theoretical work on the equilibria of differentiated product markets, such as Rosen (1974), Berry, Levinsohn and Pakes (1995), and Pakes (2003), suggests that for the general case the assumption is too strong. Unless specv is empty and the Model consists only of αt, the true conditional expectation for price need not take the proposed linear form (see Hansen (2018, ch 2)). For the hedonic case of The Standard Model, the same point is emphasised in Triplett (2004) and Brachinger, Beer and Schöni (2018).
The strength of the strict exogeneity assumption is also unnecessary. For instance, according to Diewert (2005, p 775), ‘the price statistician takes a descriptive statistics perspective’. To effect a descriptive statistics perspective in this modelling set-up requires only that the population errors are uncorrelated with the implied regressors. In the more formal econometric language of, for instance, Solon, Haider and Wooldridge (2015, p 303), a ‘projection’ is sufficient.
I make the strict exogeneity assumption because weaker versions of it will only turn out to strengthen my conclusions. It simplifies explanations as well. Later I will relax it.
2.2 The Literature Favours Weighted Estimators
After collecting, say, a large random sample of varieties, practitioners must decide how to estimate the αt.
Without more information, standard econometric practice would be to use ordinary least squares (OLS). Indeed, OLS was used for the equivalent of a static population, T = 2 set-up as early as Jevons (1869). In that case OLS produces what is now called a Jevons price index, i.e.
where V is the total number of unique varieties in the sample. Each price ratio (or ‘price relative’) is given equal weight in calculating the overall price change between periods 1 and 2.
But when quantities data are also available, influential scholars have argued against using equally weighted measures of price change for most measurement applications.
Everyone knows that pork is more important than coffee and wheat than quinine. Thus the quest for fairness lead to the introduction of weighting. (Fisher 1922, p 43)
Thus if price relatives are different, then an appropriate definition of average price change cannot be determined independently of the economic importance of the corresponding goods. (Diewert (2010, p 252) paraphrasing Keynes (1930))
… we should use a weighted regression approach, since we are interested in an estimate of a weighted average of the pure-price change, rather than just an unweighted average over all possible models, no matter how peculiar or rare. (Griliches 1971, p 8)
These views have been influential. Heravi and Silver (2007, p 251) even take weighting as ‘axiomatic’. To implement weighting, the dominant preference now is to estimate the αt with weighted least squares (WLS), using weights for economic importance. Works that support or use weighted estimation for special cases of The Standard Model include measurement handbooks from International Labour Office et al (2004) and International Labour Organization et al (2004), an econometric textbook by Berndt (1991), various statistical agency series, and countless research publications, including from recent years.
The preferred weights typically relate to expenditure shares. In a static T = 2 set-up they might look like
where qtv is for transaction quantities and the stv are expenditure shares. Estimation then produces an index number advocated by Törnqvist (1936), i.e.
(Derivations of Equations (3) and (5) are in Diewert (2005).)
The Törnqvist index is common in research applications and at national statistical offices. It is, for example, being used for an official chained measure of US consumer prices (Bureau of Labor Statistics 2018). Assessments using the so-called economic approach to index numbers shows it to have excellent properties (Diewert 1976). Judging by Clements et al (2006), the properties have further promoted WLS in other applications of The Standard Model.
The handbooks from International Labour Office et al (2004, p 301) and International Labour Organization et al (2004, p 420) also discuss an option of weighting implicitly, whereby the probability of sampling each variety reflects its economic importance. The option is equivalent to explicit weighting.
Either way, weighting for economic importance departs from mainstream econometric practices. For example, it is absent from a list of econometric justifications for weighting in Solon et al (2015), which is somewhat of a weighting handbook. Diewert (2005) also emphasises this ongoing tension between standard measurement and econometric considerations.
Occasionally the stated econometric justification for the weights is that error variance is lower for varieties with higher economic importance. For instance, Clements and Izan (1981) argue that national statistical offices might invest more resources in making accurate price measurements of varieties that command more spending. A pursuit of econometric efficiency could then justify weighting. Clements and Izan (1987) later use data on Australian consumer prices to reject the error variance hypothesis in that case.
Triplett (2004) offers another perspective, drawing on a well-known property of WLS. With exogenous weights and assumptions A1 to A4 satisfied, WLS is consistent and unbiased, just like OLS. Even if WLS is less efficient, in large samples the difference is negligible.
2.3 The Weighted Estimators are Inconsistent
Typically omitted from the conversation is that the weights are in fact endogenous. Expenditure shares contain prices, which are functions of the errors. They also contain quantities, which can be functions of the errors via prices. Either way, WLS is inconsistent because it over-represents observations with errors of a particular sign.
The justification from Triplett (2004) breaks down because it works only for exogenous weights. Arguments based on efficiency improvements are problematic too; even when the premise about error variance is correct, the efficiency benefit from weighting would have to outweigh the cost of inconsistency.
The degree of inconsistency comes from the coefficients in a so-called weighted linear projection of the errors on the regressors. That is, using δ and xtv as vector shorthand for all the coefficients and regressors that are implied in The Standard Model,
Appendix A contains a derivation. The final expectation term is not zero because the wtv are functions of the εtv.
What then transmits into the price index is the difference in the inconsistencies of the estimated fixed effects. It can be subtle. Some stylised scenarios help to develop the intuition and to set up the eventual solution. The scenarios use small samples, so the metric for central tendency switches momentarily to the degree of bias. The intuition is transferable.
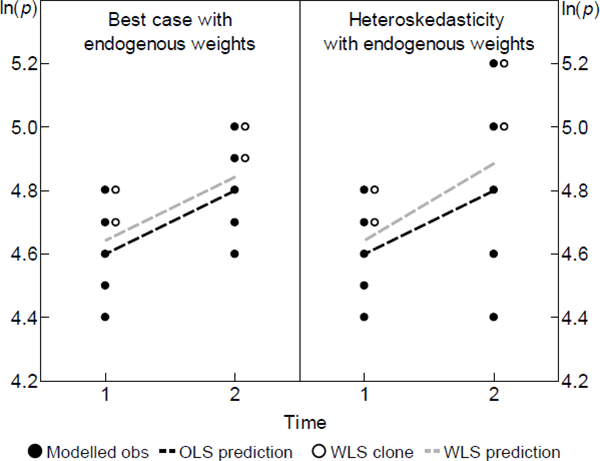
Scenarios. From a population that is static over two periods, consider a random sample of
five varieties, like the solid dots in the left panel of Figure 1. Let the
specv vector be empty, so the spread of within-period prices comes only
from the errors. In this case the strict exogeneity assumption is trivially sensible. The 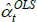 trace out a prediction
that intersects the simple arithmetic average of observed log prices in each period. The estimates are
unbiased.
trace out a prediction
that intersects the simple arithmetic average of observed log prices in each period. The estimates are
unbiased.
The left panel also introduces WLS, which is equivalent to cloning observations in numbers proportional to
their weight, before applying OLS. If in repeated samples the weights are positively related to the errors
as depicted, WLS will tend to trace out higher predictions for log prices. The 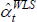 will be biased. But the key is
will be biased. But the key is 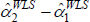 . As evident in the parallel slopes of the fitted
lines, it need not be biased. To be biased the covariance of errors and weights needs to change across the
two periods. The right panel shows that the change could arise from something so common as
heteroskedasticity.
. As evident in the parallel slopes of the fitted
lines, it need not be biased. To be biased the covariance of errors and weights needs to change across the
two periods. The right panel shows that the change could arise from something so common as
heteroskedasticity.
Some scanner data studies contain empirical comparisons of the Jevons and Törnqvist indices (Feenstra and Shapiro 2003; de Haan and van der Grient 2011; Fox and Syed 2016). Both index types are estimators for the static T = 2 version of The Standard Model, but the Törnqvist index uses endogenous weights. Since scanner data have large cross-sections, the studies can help to gauge the degree of inconsistency introduced by endogenous weighting. Fox and Syed (2016), for instance, use over 20 million observations to construct monthly price indices for basic household products, sold across six major US cities. The difference between the indices accumulates to about 12 percentage points over eleven years.
Also recall that in versions of The Standard Model for which the specv vector is non-empty, it is more realistic to assume the errors are only uncorrelated with the regressors, rather than strictly exogenous. The model parameters then describe a linear projection, not a conditional expectation. Weighting in the projection case – even if the weights are exogenous – can concentrate estimation on domains that consistently produce quite different linear projections. Hence the potential for inconsistency grows. Appendix B explains formally.
Previous mentions of the endogenous weighting issue are sparse and brief. One mention appears in Feenstra (1995), who switches immediately to using exogenous weights. Another appears in Clements et al (2006), who then point to an alternative model. Two appear in Diewert (2010), who then questions the stochastic approach to index numbers. de Haan (2004) points out that endogenous weights might be problematic in a footnote. Persons (1928) also describes the issue, although not using a stochastic framework. There being no systematic objection in the literature, endogenous WLS has remained the norm.
2.4 We Have Just Been Using the Wrong Model
The temptation here is to argue again for OLS, or maybe to seek out an instrument for expenditure shares. But the weighted estimators carefully incorporate the viewpoint of Keynes and Fisher. The problem is that the parameters of interest, as defined by the assumptions of The Standard Model, do not.
In particular, the parameters trace out the population conditional expectation of log prices. In turn, the conditional expectation operator is ignorant of the revenue profiles of each variety, putting equal emphasis on transaction prices that occur with equal probability. The macro viewpoint of Keynes and Fisher is deliberately unequal in its emphasis though. The emphasis it puts on prices depends on the expenditures that the corresponding varieties command in the market.
Although not intended to resolve the inconsistency, a more appropriate model specification has actually come up before, in Diewert (2005). An equivalent form also appears in Diewert, Heravi and Silver (2009). Its key innovation is to restate The Standard Model in units that do deserve equal emphasis. That is, if one variety has twice the economic importance of others, the model counts it as two identical varieties.
Figure 2 depicts the change informally. It reproduces the scenario in the right panel of Figure 1, now from the viewpoint of the restated model. What before were just estimator clones have become modelled observations in their own right. In other words, some (t, v) pairs are modelled to contain many of what I call units of ‘equal interest’.
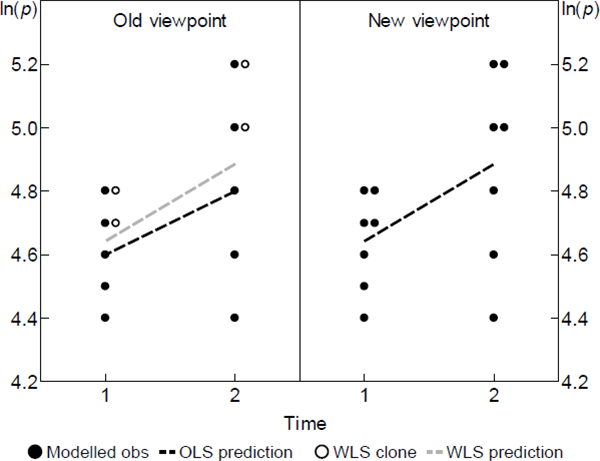
Although I have loosened some assumptions, the formal representation of the model swaps A1 and A3 with A1′ and A3′. Call this The Diewert Model.
A1′
where the new subscript u is for unit of equal interest. The total number of units in each (t, v) pair, Utv, is proportional to the preferred weight (proportionality, rather than equality, is needed to handle the non-integer weights). The other notation is unchanged, although note that αt and β will take on different values than the corresponding case of The Standard Model. I have retained the same notation to avoid a proliferation of terms. Future values of αt and β will be different again.
A3′ The errors are uncorrelated with the implied regressors.
In A1′, the new u subscript is not introducing another dimension of variation (yet), although its ability to introduce another dimension will be an advantage. Its role, for now, is to emphasise that some (t, v) pairs matter more for the identification condition in A3′ than other pairs do. It would be more natural to disaggregate into varieties, or transactions, but respecting the macro viewpoint of Keynes and Fisher calls for a population of interest with a synthetic disaggregation.
In A3′ the switch to uncorrelated errors is for realism. In Diewert's original formulation the errors were assumed to be strictly exogenous and homoskedastic. The choices reflect that the background econometric justification for the model was still an efficiency-based one.
The Standard Model is a special case of The Diewert Model, where all of the Utv are equal. For micro-oriented questions, this setting will still be appropriate. The decision can be a subtle one. For example, questions about the average price of dwellings (separate residences) call for micro models that give varieties equal emphasis, noting that each dwelling is a separate variety. Questions about the average price of housing (the infrastructure providing shelter) call for macro models with an unequal emphasis on varieties.
The Diewert Model, which is still uncommon in the literature, will be the main building block for the key results in this paper.
2.5 The Literature Contains Other Related Contributions
Although for brevity I am naming the model after Diewert (2005), the literature contains several related contributions.
Theil (1967) provides a derivation of the Törnqvist index using an original set-up. Although he does not write down a model, the expenditure weights that end up in the index do seem to come from his notion of the population of interest. The method relies on price ratios, so it does not generalise easily to multilateral comparisons and dynamic populations like The Diewert Model does. A substantial generalisation of Theil's method does appear in Diewert (2004), but the result is more cumbersome, less intuitive, and still less flexible than The Diewert Model described here.
Clements et al (2006) do write down a model, which originally comes from Voltaire and Stack (1980). It is the first to identify the right parameters, but cannot handle dynamic populations. It also lacks intuitive appeal. Appendix C elaborates on these claims.
An important and overlooked contribution has been made in an econometrics-focused paper from Machado and Santos Silva (2006). Except for its emphasis on quantity weighting (rather than expenditure weighting), the paper contains the most complete narrative on the econometric justification for measurement weights. The authors write that if the parameters of interest come from a model for prices of individual transactions, a random sample of varieties is actually endogenous. OLS is inconsistent. They further explain that WLS, with weights for transaction quantities, can unwind the inconsistency. Their insight reveals that we should view the weights in measurement estimators as corrections for endogenous sampling. This is a more conventional econometric justification for weighting, which does appear in the handbook-type article of Solon et al (2015). There should be no perceived tension between econometrics and measurement.
In some other papers the relevance of a contribution is unclear, especially where there is a tendency to blend the concepts of models and estimators.
3. Index Numbers Share Econometric Foundations
3.1 The Diewert Model Generalises Further
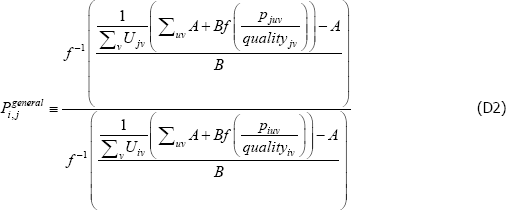
Using The Diewert Model, and equipped with a random sample of units of equal interest (i.e. sampling based on economic importance), the preferred measure of price change between two specific t (i and j) is Pij = exp 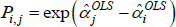 . A more general version of the same approach will turn out to be useful. It starts with a population model defined by the trivially achievable assumptions A1* to A3*.
. A more general version of the same approach will turn out to be useful. It starts with a population model defined by the trivially achievable assumptions A1* to A3*.
A1*
such that: f (·) is a strictly monotonic function; ptuv, αt, εtuv, Utv are understood already; and qualitytv is some strictly positive scalar used to standardise the price of variety v at time or territory t. Remember the αt need not take the same values as in the previous models. Moreover, the αt can change with, say, different choices of f (·) (more on this below).
A2* Across varieties the observations are independently and identically distributed.
A3* The errors are uncorrelated with the implied regressors. Note that the implied regressors are now just dummies for t, which means that strict error exogeneity is also satisfied, for free. Moving quality to the left-hand side also allows it to be defined more loosely than was exp(β′specv).
Interest then lies in the quality-adjusted price index
The corresponding index measure becomes
And since the 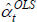 will just be arithmetic sample averages,
will just be arithmetic sample averages,
Equation (11) is a ratio of what in the mathematics literature are called Kolmogorov or quasi-arithmetic means (see Fodor and Roubens (1995)). The role of f (·) is to pin down the specific type of mean, or average. A more intuitive form for the index is thus
The average operator might be, for instance, the arithmetic mean (equivalent to f (x) = x), the geometric mean (f (x) = ln(x)), or the harmonic mean (f (x) = x − 1). Although in a cosmetically different format, the same generalised approach to averaging actually appears in recent measurement work by Brachinger et al (2018).
The specific cases of 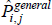 , and the target index
, and the target index 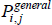 , are differentiated by distinct choices for the type average (f (·)), what merits equal interest ({Utv}), and what defines the quality of varieties ({qualitytv}). Stress is on distinct because some choices are always equivalent:
, are differentiated by distinct choices for the type average (f (·)), what merits equal interest ({Utv}), and what defines the quality of varieties ({qualitytv}). Stress is on distinct because some choices are always equivalent:
- Choosing any function f (·) is equivalent to choosing any of its affine transformations A + B(f (·)).
- Any transformations of {Utv} that preserve the relative emphasis on varieties within t do not matter. So choosing any {Uiv, Ujv} is equivalent to choosing transformations of the type {CUiv, DUjv}, where C and D are strictly positive scalars.
- For f (x) = ln(x) and all f (x) = xθ, where θ is a non-zero real number, choosing any {qualitytv} is equivalent to choosing any of its linear transformations {Hqualitytv}, where H is a strictly positive real number.
Appendix D substantiates the first two claims. The third comes from a linear homogeneity result originally established by Nagumo (1930).
3.2 Three Choices Distinguish Price Index Functions
The literature contains hundreds of different bilateral and multilateral price index functions. Most, if not all, are recorded or referenced across publications by Fisher (1922), Sato (1974), Banerjee (1983), Bryan and Cecchetti (1994), Hill (1997), Balk (2008), von Auer (2014), Rao and Hajargasht (2016), Gábor-Tóth and Vermeulen (2017) and Redding and Weinstein (2018). Some come from intuition and experimentation, and some from derivations using the economic approach. Yet it turns out – and this is the central contribution of the paper – that the simple identity in Equation (12) describes practically all of them.
More precisely, the identity in (12) describes at least all of the recorded price index functions that:
- treat t as discrete. This excludes a continuous time index from Divisia (1926).
- are explicit. This excludes types that are defined uniquely as the residual of a quantity index. The most prominent example is the so-called implicit Törnqvist price index, discussed in Diewert (1992).
- are not the esoteric bilateral types that were proposed in work by Montgomery (1937), Stuvel (1957), and Banerjee (1983), or early multilateral types that were excluded from a taxonomy of multilateral indices in Hill (1997). (Balk (2008, p 35) provides the references for these multilateral exceptions, starting with Theil (1960) and Kloek and de Wit (1961)).
This result is related to the main contribution of a paper by de Haan and Krsinich (forthcoming), which is to show that some seemingly quite different bilateral functions can be understood as averaging quality-adjusted prices. Their finding is nested in the generalisation here. Also note that, with time, the carve outs listed above could still turn out to comply with the paradigm. They are not yet proven exceptions.
Table 1 lists some of the complying bilateral functions and their settings for f (x), {Utv}, and {qualitytv}. Emphasis is on types that are most important to measurement practitioners, based on my judgement and the results of a statistical agency survey in Stoevska (2008). The table also lists some for their unusual forms. It omits types that are averages of others, such as a celebrated ‘ideal’ function from Fisher (1922, p 142 Formula 153).
| Index name (year) | f (x) | qualitytv | Utv | |
|---|---|---|---|---|
| Dutot (1738) | x | zv ∈ℝ++ | qualitytv | |
| Carli (1764) | x | p1v | 1 | |
| ⋮ | ⋮ | x − 1 | p2v | 1 |
| Jevons (1863) | ln(x) | zv ∈ℝ++ | 1 | |
| Coggeshall (1886) | x − 1 | p1v | 1 | |
| ⋮ | ⋮ | x | p2v | 1 |
| Laspeyres (1871) | x | zv ∈ℝ++ | qualitytvq1v | |
| ⋮ | ⋮ | x | p2v | qualitytvqtv |
| ⋮ | ⋮ | x − 1 | p1v | p2vq1v |
| Paasche (1874) | x | zv ∈ℝ++ | qualitytvq2v | |
| ⋮ | ⋮ | x | p1v | qualitytvqtv |
| ⋮ | ⋮ | x − 1 | p2v | p1vq2v |
| Walsh (1901, type a) | x | zv ∈ℝ++ | ||
| Fisher (1922, Formula 33) | x | p1v | ∈(0,1) | |
| ⋮ | ⋮ | x − 1 | p2v | ∈(0,1) |
| Törnqvist (1936) | ln(x) | zv ∈ℝ++ | 0.5(s1v + s2v) | |
| Lloyd (1975)–Moulton (1996) | x1 − σ | p1v | qualitytvq1v | |
| Sato (1976)–Vartia (1976) | ln(x) | zv ∈ℝ++ | ||
| Redding and Weinstein (2018) | ln(x) | 1 | ||
| ⋮ | ⋮ | ln(x) | ψv | |
|
Notes: The Dutot, Carli, Laspeyres, Paasche and Moulton attributions have all been taken on authority of Balk (2008); zv ∈ℝ++ is intended to mean that any strictly positive definitions of quality that are fixed across t, are admissible; is a weighted median of the items in set {xv}, using weights of yv (the notation is non-standard); the notation ∈(0,1) reflects that in median- and mode-based functions, only one observation has a non-zero weight; ; σ is a consumer elasticity of substitution; the index from Redding and Weinstein (2018) is what the authors refer to as the ‘common goods’ index; ψtv is a time-varying preference parameter, explained further in the original paper |
||||
Notice that many types correspond to several distinct combinations of f (x), {Utv}, and {qualitytv}. To exhaustively list the combinations associated with each type is a difficult problem, left for future work. The result of that work might be surprising. To illustrate, Appendix E includes a derivation from Bert Balk (pers comm, 16 March 2018) that generates an unexpected combination for the Dutot function. Knowing all of the combinations would help for comparing the merits of the functions, because it would demonstrate the breadth of relevant measurement preferences for which each function is exact.
Still, it is clear that at least some types cover every possible {qualitytv} that is fixed over t. This quality-robust feature adds to their appeal. Otherwise the functions tend to gauge qualitytv through relative prices. To gauge qualitytv like this is an objective choice.[1]
A notable exception for the way it gauges qualitytv is a static-population function from Redding and Weinstein (2018). It uses expenditure shares and allows qualitytv to vary over t. Derived using the economic approach, the function aims to measure cost of living changes under dynamic preferences. Using expenditure to gauge product quality like this has strong parallels in the international trade literature. (Notable examples are papers by Khandelwal (2010) and Feenstra and Romalis (2014)).
Work by von Auer (2014) outlines a so-called Generalised Unit Value Index Family, which is relevant here as well. Using the framework of this paper, the Family members are functions for which f (x) = x, {qualitytv} is fixed over t within varieties, and Utv = qualitytvqtv for all (t, v) pairs. (von Auer introduced axioms for sensible quality definitions as well.) Examples in the table are the indices of Paasche and Laspeyres. The Family is special because the implied quantity index is always the growth in the number of units of equal interest, which, in turn, are just the amounts of transacted quality. This is an intuitive, appealing feature, and one way to interpret official measures of output growth in, for instance, Australia and the United Kingdom.
The literature on multilateral functions is more niche. Table 2 lists examples of some of the types, from different parts of the taxonomy in Hill (1997). Rao and Hajargasht (2016) summarise how several of them are used to calculate official purchasing power parity statistics from the World Bank. The table does the measures a disservice because there is a lot of ingenuity behind qualitytv definitions that I have had to abbreviate to 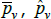 , and
, and 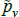 . Actually, while not the intention of the developing authors, those quality definitions all correspond to efficient method of moments estimates. This result is an adaptation of insights from work by Rao and Hajargasht (2016) (adapted because our stochastic approaches are different). Only the
. Actually, while not the intention of the developing authors, those quality definitions all correspond to efficient method of moments estimates. This result is an adaptation of insights from work by Rao and Hajargasht (2016) (adapted because our stochastic approaches are different). Only the 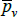 result, relating to the Geary-Khamis index, is new. Details are in Appendix F.
result, relating to the Geary-Khamis index, is new. Details are in Appendix F.
| Index name (year) | f (x) | qualitytv | Utv | |
|---|---|---|---|---|
| Walsh (1901, type b) | ln(x) | zv ∈ℝ++ | ||
| Walsh (1901)–Van Ijzeren (1956) | x | zv ∈ℝ++ | ||
| ⋮ | ⋮ | x − 1 | piv | |
| Geary (1958)–Khamis (1972) | x | qualitytvqtv | ||
| ⋮ | ⋮ | x − 1 | ptvqtv | |
| Rao (1990) | ln(x) | stv | ||
| Hajargasht and Rao (2010, type a) | x | stv | ||
|
Notes: zv ∈ℝ++ is intended to mean that any strictly positive definitions of quality that are fixed across t, are admissible; the Van Ijzeren attribution is taken on authority of Balk (2008); precise definitions of are available in Appendix F; see Hill (1997) for details on |
||||
3.3 This Changes the Stochastic Approach
Throughout this paper, measurement objectives have been defined using parameters from econometric models. Econometric estimators have then justified the corresponding measurement tools. When the population of varieties being transacted is static, the process is synonymous with the stochastic approach to choosing index functions.
To date the stochastic approach has been less influential than the economic and test approaches. It is actually more commonly used as an econometric gateway for generalising Jevons- and Törnqvist-type functions to dynamic populations. Hence the widespread popularity of The Standard Model. The approach has also been used as a means to calculate confidence intervals, to gauge index reliability (see, for instance, Rao and Hajargasht (2016)).
Judging by Clements et al (2006), the lack of influence comes partly from reservations about the stated econometric justifications for weighting. The occasional discomfort over weight endogeneity has also mattered somewhat. Section 2 has shown that both objections are fair, but resolvable. The econometric model just needs to define the parameters of interest carefully.
The new framework presented here has extended the approach in other ways as well:
- The approach now has a wider scope. It covers practically all existing price index functions and infinitely more. So it is a more complete tool for comparing them. A repercussion is that index types formerly considered as stochastic-compatible are no longer special for that reason.
- Albeit not always in a unique way, the approach now distinguishes index types by their conceptual characteristics. Previously the approach distinguished types by somewhat arbitrary modelling assumptions.
- Being specified in terms of prices, rather than price ratios, there is no built-in need for static populations that produce matched price pairs. The approach is hence a means to carry standard index function perspectives over into dynamic populations. (Some compromises are necessary, and will be discussed further in Section 4.2.)
The changes, in turn, provide an alternative means of understanding and communicating measurement challenges to economic researchers that do not have specialist backgrounds in measurement. Consider the phenomenon of chain drift, which occurs in index functions that provide different results under chained comparisons than under direct ones (see Ivancic, Diewert and Fox (2011)). The chained and direct indices imply different populations of interest, because they have different units of equal interest. Using either set-up as the correct benchmark, the gap between them can be viewed as reflecting endogeneity.
In some cases, the changes can also open new avenues for tackling measurement problems. The next section discusses three examples, and some obvious avenues for further progress. As the discussion is targeted at measurement specialists, applied macro researchers can skip comfortably to the conclusion.
4. The New Framework Challenges Some Practices
4.1 The Goldberger (1968) Bias Correction is Unnecessary
For models with a semi-log form, like The Standard Model, the international consumer and producer price index manuals recommend a bias correction for 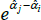 (International Labour Office et al 2004, p 118; International Labour Organization et al 2004, p 184). Following Goldberger (1968), the correction is to account for the fact that
(International Labour Office et al 2004, p 118; International Labour Organization et al 2004, p 184). Following Goldberger (1968), the correction is to account for the fact that
The Diewert Model is also semi-log, so the same applies. The proposed bias-corrected estimator is
where Vâr (·) is estimated variance. The correction matters most when the variance of 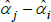 is largest, which, in turn, is more likely for cases with small sample sizes and few controls. An empirical illustration in Kennedy (1981) shows the correction to make a small difference. More measurement-focused illustrations in Syed, Hill and Melser (2008) and de Haan (2017), show it to make a trivial difference. However, these examples use large samples and many controls. As pointed out by Hill (2011), we cannot rule out there being cases for which the correction is material.
is largest, which, in turn, is more likely for cases with small sample sizes and few controls. An empirical illustration in Kennedy (1981) shows the correction to make a small difference. More measurement-focused illustrations in Syed, Hill and Melser (2008) and de Haan (2017), show it to make a trivial difference. However, these examples use large samples and many controls. As pointed out by Hill (2011), we cannot rule out there being cases for which the correction is material.
But even in cases where the bias correction matters, is it sensible? Here I show that it seems to imply incompatible analytical preferences.
With the αt coming from a semi-log model, defining the measurement objective as 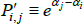 is just articulating that the preferred measure of central tendency is a geometric average. In particular, taking a finite view of the population, which is a common choice in the measurement literature, revealed preference is for a ratio comparison of
is just articulating that the preferred measure of central tendency is a geometric average. In particular, taking a finite view of the population, which is a common choice in the measurement literature, revealed preference is for a ratio comparison of
For a more standard, continuous view of the population, the corresponding geometric-type averages look more complicated. They are
where F(·) is a cumulative density function and the integrals are over u and v.
If interest is in geometric-type averages like these, why then would we subject 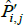 to a standard test of unbiasedness, which is an arithmetic criteria of central tendency? Logical consistency would dictate the use of a compatible, geometric criteria.
to a standard test of unbiasedness, which is an arithmetic criteria of central tendency? Logical consistency would dictate the use of a compatible, geometric criteria.
It turns out that with a geometric criteria a correction is unnecessary. In particular,
where 𝔼geometric [·] is a geometric type of expectation operator and F(·,·) is a cumulative density function.
The natural follow-up question is whether compatible criteria of central tendency always generate such benign results. The answer: not necessarily.
To illustrate, let 𝔼* denote an expectation operator that is logically consistent with the choice of f (·), such that
Now let f (x) = xθ, where θ is a non-zero real number. Along with f (x) = x, this setting for f (x) covers all of those that currently appear in the measurement literature. Denote the corresponding index and target as 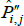 and
and 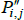 . Generally it will be the case that
. Generally it will be the case that
There are, however, important special cases. In particular, many indices use definitions of quality for which qualitytv = priceiuv for all t, u, and v. In that case it always holds that 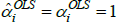 =1. Hence
=1. Hence
This is an unusual result. It means that for indices like Paasche, interpretations that set qualitytv = priceiuv are more achievable in small samples than other interpretations.
4.2 Some Dynamic Population Methods Look Questionable
In durable goods markets especially, the norm is for the population of transacted varieties to be dynamic. Yet index functions, the primary tools of economic measurement, are designed for static populations of varieties.
A crude workaround is to drop orphan varieties. However, the prevailing view in the field of measurement is that orphan status is non-random. Dropping the orphans generates what is akin to another endogenous sampling problem. More sophisticated methods are needed. According to Triplett (2004, p 9), handling quality change that comes from a changing population has ‘long been recognised as perhaps the most serious measurement problem in estimating price indexes’. Moulton (2017) explains how successive investigations have estimated that the problem accounts for the largest source of measurement bias in the US consumer price index.
The updated stochastic approach presented here offers a useful perspective on the problem. As shown below, without any intrinsic dependence on price ratios, it provides avenues through which to extend index function principles to dynamic populations. It is also a means to identify existing dynamic population methods that are incompatible with the (stochastic approach) principles behind index functions.
When extending to dynamic populations, not all of the features of index functions can be preserved, and compromises are necessary:
-
Some choices of {qualitytv} become undefined. In particular, {qualitytv} cannot be benchmarked to prices if some of them are missing from the population. In this case, the missing transaction prices that are needed to fully define {qualitytv} might defensibly be viewed as having synthetic values, each corresponding to what might have been the price had the variety been transacted.
In the estimation phase, coming up with these values is often called ‘patching’ or ‘imputing’. The measurement literature already contains many approaches to patching (see International Labour Office et al (2004), International Labour Organization et al (2004), and Eurostat (2013)).
- Section 3.2 showed that, in static populations, some distinct combinations of f (x), {Utv}, and {qualitytv} coincide with others. The same feature breaks down in dynamic populations. So practitioners looking to generalise an index function to a dynamic population must choose just one combination. Alternatively, they could choose several combinations, calculate a separate index for each, and take an average. The latter approach is similar in spirit to, say, the ideal index from Fisher (1922).
Strategies like these are already being used. For instance, when constructing an index directly from a dynamic population version of The Standard Model, practitioners are implicitly choosing a single definition for {qualitytv}, based on a least squares criteria. Using the method of moments approach outlined in Rao and Hajargasht (2016) (examples are in Appendix F), a least squares criteria for choosing {qualitytv} could be executed under all sorts of other settings for f (x) and {Utv}.
The literature contains criticisms of this direct method, which have stifled take-up by national statistical offices. The key criticism is ultimately about the definition of quality. For instance, in 2002, responding to a request by the US Bureau of Labor Statistics (BLS), a panel of experts wrote:
Recommendation 4-4: BLS should not allocate resources to the direct … method (unless work on other hedonic methods generates empirical evidence that characteristic parameter stability exists for some products). (National Research Council 2002, p 143)
The concern is that restricting the coefficients on variety specifications to be fixed over time is unlikely to reflect the true conditional expectation function for prices. Several papers have rejected parameter stability for the computer market in the United States (Berndt and Rappaport 2001; Pakes 2003), and have echoed the panel's recommendation (see also Diewert et al (2009) and Hill (2011)).
Viewed through the updated stochastic approach, this argument looks problematic for two reasons:
- The objection really is to fixing the quality definition across t, within varieties. Yet the same is true of all common index numbers. If fixing each variety's quality definition is indeed a drawback, index function choices need to be reconsidered too. Functions with quality definitions that change over t, like the common goods index from Redding and Weinstein (2018), would need to become more mainstream.
- To repeat a point made already, there is no need for the model to describe the conditional expectation function exactly (i.e. requiring the errors to be strictly exogenous to the regressors). It is sufficient for the model to identify useful descriptive statistics (i.e. accepting errors that are only uncorrelated with the regressors).
Moreover, the proposed alternatives do not actually address the fixed quality problem. For instance, the most popular alternative is to use synthetic values for all missing transaction prices, not just the missing prices needed to define quality. Standard index functions can then be applied. However, no matter where those synthetic values come from, the index functions that are typically applied to the new population still take constant quality perspectives. Moreover, the interpretation of the final index is no longer an average of quality-adjusted actual prices. Instead it is
where the ¬juv indexes fictitious product observations, from the additional patching. The same issue transfers to the population target. (Conditions under which the additional patching makes no difference are provided in de Haan (2008).)
Diewert et al (2009) examine and propose another alternative, which they show is also equivalent to the so-called characteristics prices method. The method is fully consistent with the new stochastic approach presented in this paper, it being akin to calculating indices for several combinations of f (x), {Utv}, and {qualitytv}, before taking an average. Still, the underlying quality definitions are fixed over time.
Note that Feenstra (1994), Ueda, Watanabe and Watanabe (2016), and Redding and Weinstein (2018) introduce other, deterministic methods to handle dynamic populations. The methods do not seem to have obvious connections to the stochastic approach presented here, but are justified by the economic approach.
Occasionally, the literature also defines dynamic population indices using models that are like The Standard Model, except that the dependent price variable is in levels, rather than logs. Since this set-up is obviously not a special case of Equation (8), it is also in conflict with the principles behind the stochastic approach.
4.3 Unit Values Can Distort Index Number Interpretation
So far we have assumed that each (t, v) pair has a single price. The assumption is unrealistic in the general case, even with fully efficient markets. For instance, each t is an area, not a point, in space or time. A price shock can fall easily within its boundaries. How should measurement methods handle breaches of the single price assumption?
Current practice, stemming from Walsh (1901), Fisher (1922) and Davies (1932), is to specify measurement tools in terms of ‘unit values’ (see International Labour Office et al (2004) and International Labour Organization et al (2004)). Regardless of the situation, the unit values are always equal to the total measured expenditure on each (t, v) pair, divided by the number of units transacted. That is, letting 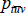 denote the unit value for pair (t, v),
denote the unit value for pair (t, v),
where the subscript n tracks each of the individual transactions. Unit values are hence quantity-weighted, arithmetic averages of prices.
The attraction of the unit values solution is that it can shoehorn reality into the traditional formulation of index functions. Moreover, it has low information requirements, needing only total expenditures (numerator) and numbers of transactions (denominator) for each variety. But the functions – and their population targets – are then comparing averages of quality-adjusted unit values at different points in space or time. Are there sensible ways to preserve a cleaner interpretation, about quality-adjusted raw prices? Would the outcomes even be different?
With its more flexible formulation, the new stochastic approach framework presented in this paper is an avenue through which to tackle these questions. Diewert (2004) and Rao and Hajargasht (2016) also noted the potential of stochastic approaches to handle raw prices if they are available.
Preserving the raw prices interpretation requires only that, for each variety in a given time period, the units of equal interest are allocated to the different transaction prices somehow. Since each of the transactions for a variety are (definitionally) for a homogeneous product, it seems the only sensible solution is to allocate units of equal interest in proportion to the number of transactions executed at each price. Sometimes this will correspond to the unit values solution, but sometimes it will not.
To illustrate, I will focus on index functions, rather than their population targets. The same ideas carry over easily though.
Denote the index that uses raw prices as
and the one that uses unit values as
The indices are equivalent if
Letting f (x) = x, a common choice for many indices, the condition reduces to
Now, use S to denote some strictly positive scalar, and allocate the units of equal interest evenly across each transaction. The raw prices calculation on the left-hand side of Equation (34) becomes
The result does indeed correspond to the unit values solution on the right-hand side of Equation (34). The unit value method looks ideal.
For other choices of f (x) the unit value method looks less benign. For instance, consider the choice of f (x) = ln(x). Equivalence to the raw prices method is guaranteed only when
If units of equal interest are allocated evenly across transactions, the raw prices solution on the left-hand side becomes
Equivalence to the unit values method is unlikely to hold, since
When there is any variation in transaction prices for a given (t, v) pair, the inequality is strict (Balk 2008, p 70).
So for some types of f (x), the unit value method necessarily changes the interpretation of the index, or can be seen as distorting the true index. This should be unsurprising; the unit value method takes a position on the appropriate measure of central tendency without considering the choice of f (x), which is also a position on the appropriate measure of central tendency.
4.4 There Are Obvious Avenues for Further Progress
In establishing the new stochastic framework, and the results that come from it, this paper has left many obvious questions unanswered:
- Can we determine exactly how many distinct combinations of f (x), {Utv}, and {qualitytv} correspond to each price index? And can we be precise about what those are? The answers would be useful for comparing the merits of various functions. They might also yield new options for handling dynamic populations.
- Can we definitively rule out some indices from complying with the stated paradigm? If so, is this a problem with the paradigm or the index?
- What corrections are sensible for the measurement approaches that have undesirable central tendencies in small samples? Would the corrections ever be material enough to promote for use at national statistical offices?
- How material in practice are the unit value distortions that I have identified?
- What does the new framework imply for appropriate confidence intervals? Do the implications align with existing work on index number uncertainty, such as Crompton (2000), Clements et al (2006), and Rao and Hajargasht (2016)?
- Should the same perspectives on the population of interest be incorporated elsewhere in the empirical macro literature?
These are potentially fruitful subjects for future work. The final one is the topic of a forthcoming paper. With time, the deeper connections to the econometric literature might reveal other opportunities.
5. Conclusion
There is a material difference between modelling, say, the price of dwellings (distinct residences), and the price of housing (the infrastructure providing shelter). Modelling the price of housing is a more macro-oriented task and implies a synthetic population of interest. A simple way to implement the macro orientation is to write the model in terms of what I call units of equal interest.
In the field of economic measurement it is common to model prices from macro perspectives, so units of equal interest come up a lot. In fact this paper shows that practically all price index functions are defined by their choice of average, their definition of quality, and their stance on equal interest. For instance, the Törnqvist function, used in the official chained version of the US consumer price index, is defined by the geometric average, any definitions of quality that are constant over adjacent time periods, and units of equal interest that are proportional to expenditure shares. The Laspeyres function, used in the Australian consumer price index, is defined by the arithmetic average, definitions of quality that are proportional to (closing period) prices, and units of equal interest that are proportional to transacted amounts of quality.
This new framework for differentiating between index functions is free of ambitious modelling assumptions. Hence it is more defensible and conceptual than the so-called stochastic approaches that preceeded it. By covering practically all index functions, it is also more comprehensive. And the time investment needed to understand it is small. This hopefully makes it useful for other macro researchers wanting to appreciate the strengths and weaknesses of the tools they are routinely using.
For measurement specialists, the new framework might offer new avenues to understand and tackle measurement problems. To illustrate, I use it to challenge the use of the Goldberger (1968) bias correction, the widespread reliance on unit values, and some common views on quality adjustment with dynamic populations. At a high level, this work is a stochastic complement to recent research on the economic approach to index functions by Redding and Weinstein (2018), because it unifies a wide range of measurement methods.
Appendix A: The Inconsistency Arising from Endogenous Weighting is a Linear Projection
Let δ and xtv be vector shorthand for the full set of coefficients and regressors that are implicit in The Standard Model, for a given (t, v) pair. Then
Applying the Law of Large Numbers and the Continuous Mapping Theorem (see Hansen (2018)),
The right-hand side of Equation (A3) is a weighted linear projection of the errors on the regressors. Since the weights are functions of errors, the second expectation term is not zero.
Appendix B: Loosening Strict Error Exogeneity Introduces Another Avenue for Weights to Generate Inconsistency
Consider weights that are exogenous, being functions only of the regressors. Retain the strict error exogeneity assumption. Using the law of iterated expectations, Equation (A3) becomes
So there is no inconsistency. But without strict error exogeneity, Equation (B3) does not follow from Equation (B2). Consistency is not guaranteed, even with well-behaved weights.
Appendix C: The Model of Voltaire and Stack (1980) Equates to The Diewert Model, under Restrictive Conditions Only
Using my notation and making some trivial generalisations, the model of Voltaire and Stack (1980) swaps A1′ for A1″.
A1″
where V* is the number of varieties in a population viewed to be finite (as opposed to the more common, superpopulation viewpoint).[2]
In the original application the population is static and wjv = wiv for all i and j. If also 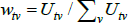 , as looks to be the intention, the model identifies the same αj – αi as the equivalent case of The Diewert Model. Otherwise the relevance of the Voltaire and Stack model is easy to break.
, as looks to be the intention, the model identifies the same αj – αi as the equivalent case of The Diewert Model. Otherwise the relevance of the Voltaire and Stack model is easy to break.
To illustrate, note that under the above conditions, for any i ≠ j, the key assumptions of the Voltaire and Stack model can be rewritten in the form
and
Therefore
Since the Voltaire and Stack model views the population as finite, with V* varieties,
Under the same conditions, The Diewert Model implies
where
Taking the same finite perspective on the population,
which mirrors the result for the Voltaire and Stack model.
However, if the population is, for instance, dynamic, the equivalence does not hold. Actually it is not even clear how to define the parameters, particularly V*. One option might be to take an arithmetic average of the variety counts in each t, but even here the model produces unusual results. To illustrate, let β′specv =0 and consider a finite population described by
The Voltaire and Stack model identifies the parameters to be
and
These are nonsensical results, particularly the second, being outside the range of population prices in t = 2. The equivalent figures for The Standard Model are α1 = 6 and α2 = 7.
The other drawback of the Voltaire and Stack model is its lack of conceptual appeal. The authors do not justify the relevance of the dependant variable, so it is unclear why the coefficients are interesting.
Appendix D: Some Choices of f (x), {Utv}, and {qualitytv} are Always Equivalent
In
let g(·) = A + Bf (·), where A and B are scalars.
Then
So choosing any function f (·) is always equivalent to choosing any of its affine transformations A + B(f (·)).
Now let 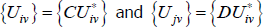 , where C and D are strictly positive scalars.
, where C and D are strictly positive scalars.
The identity in Equation (11) becomes
So for {Utv}, changes to the relativities across t do not matter.
Appendix E: The Dutot Index Has an Unexpected Interpretation
Aside from the combination listed in Table 1, the Dutot price index corresponds to the choices f (x) = ln(x), qualitytv = zv ∈ℝ++, and 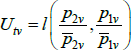 Here l(·,·) is the logarithmic mean, defined as
Here l(·,·) is the logarithmic mean, defined as
The result draws on Balk (2008, p 193), and the proof from personal correspondence with Bert Balk (pers comm 16 March 2018).
Start with the identity
It follows that
Applying linear homogeneity of the logarithmic mean,
From here the rest is clear.
Appendix F: The Method of Moments Makes Sensible Multilateral Index Functions
Consider a model consisting of assumptions A1** to A4**. It is a special case of The Diewert Model.
A1**
where: f (·), ptuv, αt, εtuv and Utv are understood already; and λv is a fixed effect for varieties.
A2** Across varieties the observations are independently and identically distributed.
A3** The errors follow strict exogeneity of the form. So
A4** There is conditional heteroskedasticity of the form
where σ is some strictly positive constant.
Now consider a case that sets f (x) = x, Utv = qtvλv and 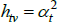 . As the model is in levels, the heteroskedasticity assumption is natural.
. As the model is in levels, the heteroskedasticity assumption is natural.
The model corresponds to the conditional moment restriction
where δ and xtv is vector shorthand for the full set of coefficients and regressors (the time and product dummies) that are implicit in the model, for a given (t, v) pair.
Following Wooldridge (2010, p 542), the efficient method of moments estimators for αt and λv solve
But note that
and
the last of which contains the unknown parameters α and λ. The feasible method of moments estimators use 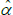 and
and 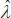 instead.
instead.
The resulting system of equations is
and
This is the same as the system of Geary (1958) and Khamis (1972). The result differs somewhat from the original method of moments derivation of Rao and Hajargasht (2016), who argue that an inefficient weighting system is necessary to generate the index. Although our set-ups are different, ultimately it is the introduction of units of equal interest that resolves the discrepancy.
Table F1 provides the settings needed to generate the other multilateral indices considered in Rao and Hajargasht (2016), using the method of moments. I have not explored whether there are further multilateral indices that fit the method of moments interpretation.
| Index name (year) | 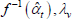 |
f(x) | Utv | htv |
|---|---|---|---|---|
| Dutot-style | 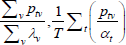 |
x | λv | 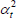 |
| Harmonic | 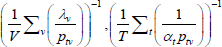 |
x−1 | 1 | 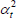 |
| Geometric | 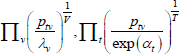 |
ln(x) | 1 | 1 |
| Geary (1958)–Khamis (1972) | 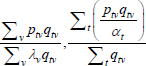 |
x | λvqtv | 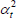 |
| Iklé (1972) | 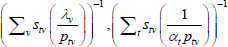 |
x−1 | ptvqtv | 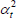 |
| Rao (1990) | 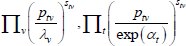 |
ln(x) | ptvqtv | 1 |
| Hajargasht and Rao (2010, type a) | 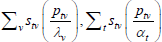 |
x | ptvqtv | 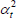 |
| Hajargasht and Rao (2010, type b) | 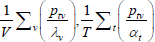 |
x | 1 | 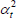 |
References
Australian Bureau of Statistics (2005), ‘The Introduction of Hedonic Price Indexes for Personal Computers’, Information paper, ABS Cat No 6458.0.
Balk BM (2008), Price and Quantity Index Numbers: Models for Measuring Aggregate Change and Difference, Cambridge University Press, Cambridge.
Banerjee KS (1983), ‘On the Existence of Infinitely Many Ideal Log-Change Index Numbers Associated with the CES Preference Ordering’, Statistische Hefte, 24(1), pp 141–148.
Berndt ER (1991), The Practice of Econometrics: Classic and Contemporary, Addison-Wesley, Reading.
Berndt ER and NJ Rappaport (2001), ‘Price and Quality of Desktop and Mobile Personal Computers: A Quarter-Century Historical Overview’, The American Economic Review, 91(2), pp 268–273.
Berry S, J Levinsohn and A Pakes (1995), ‘Automobile Prices in Market Equilibrium’, Econometrica, 63(4), pp 841–890.
Brachinger HW, M Beer and O Schöni (2018), ‘A Formal Framework for Hedonic Elementary Price Indices’, AStA Advances in Statistical Analysis, 102(1), pp 67–93.
Bryan MF and SG Cecchetti (1994), ‘Measuring Core Inflation’, in NG Mankiw (ed), Monetary Policy, NBER Studies in Business Cycles, Vol 29, The University of Chicago Press, Chicago, pp 195–215.
Bureau of Labor Statistics (2017), ‘Quality Adjustment in the CPI’, viewed 11 February 2018. Available at <https://www.bls.gov/cpi/quality-adjustment/home.htm>.
Bureau of Labor Statistics (2018), ‘Chapter 17. The Consumer Price Index’, Handbook of Methods, rev 14 February 2018, Bureau of Labor Statistics, Washington DC, viewed 16 February 2018. Available at <https://www.bls.gov/opub/hom/pdf/homch17.pdf>.
Clements KW and HY Izan (1981), ‘A Note on Estimating Divisia Index Numbers’, International Economic Review, 22(3), pp 745–747.
Clements KW and HY Izan (1987), ‘The Measurement of Inflation: A Stochastic Approach’, Journal of Business & Economic Statistics, 5(3), pp 339–350.
Clements KW, HY Izan and EA Selvanathan (2006), ‘Stochastic Index Numbers: A Review’, International Statistical Review, 74(2), pp 235–270.
Coggeshall F (1886), ‘The Arithmetic, Geometric, and Harmonic Means’, The Quarterly Journal of Economics, 1(1), pp 83–86.
Court AT (1939), ‘Hedonic Price Indexes with Automotive Examples’, The Dynamics of Automobile Demand, General Motors Corporation, New York, pp 98–117.
Crompton P (2000), ‘Extending the Stochastic Approach to Index Numbers’, Applied Economics Letters, 7(6), pp 367–371.
Davies GR (1932), ‘Index Numbers in Mathematical Economics’, Journal of the American Statistical Association, 27(177A), pp 58–64.
de Haan J (2004), ‘Hedonic Regression: The Time Dummy Index as a Special Case of the Imputation Törnqvist Index’, Paper presented at the 8th Ottawa Group Meeting on Price Indices, Helsinki, 23–25 August.
de Haan J (2008), ‘Hedonic Price Indexes: A Comparison of Imputation, Time Dummy and Other Approaches’, University of New South Wales, Centre for Applied Economic Research Working Paper 2008/01.
de Haan J (2017), ‘A Note on Bias Adjustment of the Time Dummy Hedonic Index’, Background paper prepared for the Centre for Applied Economic Research EMG Workshop 2017, Sydney, 1 December.
de Haan J and F Krsinich (forthcoming), ‘Time Dummy Hedonic and Quality-Adjusted Unit Value Indexes: Do They Really Differ?’, The Review of Income and Wealth.
de Haan J and HA van der Grient (2011), ‘Eliminating Chain Drift in Price Indexes Based on Scanner Data’, Journal of Econometrics, 161(1), pp 36–46.
Diewert WE (1976), ‘Exact and Superlative Index Numbers’, Journal of Econometrics, 4(2), pp 115–145.
Diewert WE (1981), ‘The Economic Theory of Index Numbers: A Survey’, in A Deaton (ed), Essays in the Theory of Consumer Behaviour: In Honour of Sir Richard Stone, Cambridge University Press, Cambridge, pp 163–208.
Diewert WE (1992), ‘Fisher Ideal Output, Input, and Productivity Indexes Revisited’, Journal of Productivity Analysis, 3(3), pp 211–248.
Diewert WE (2004), ‘On the Stochastic Approach to Linking the Regions in the ICP’, University of British Columbia, Department of Economics Discussion Paper No 04-16. Available at <https://econ.sites.olt.ubc.ca/files/2013/06/pdf_paper_erwin-diewert-notes-stochastic-approach.pdf>.
Diewert WE (2005), ‘Adjacent Period Dummy Variable Hedonic Regressions and Bilateral Index Number Theory’, Annales d'Économie et de Statistique, 79/80, pp 759–786.
Diewert WE (2010), ‘On the Stochastic Approach to Index Numbers’, in WE Diewert, BM Balk, D Fixler, KJ Fox and AO Nakamura (eds), Price and Productivity Measurement: Volume 6 – Index Number Theory, Trafford Press, Bloomington, pp 235–262.
Diewert WE, S Heravi and M Silver (2009), ‘Hedonic Imputation versus Time Dummy Hedonic Indexes’, in WE Diewert, JS Greenlees and CR Hulten (eds), Price Index Concepts and Measurement, NBER Studies in Income and Wealth, Vol 70, University of Chicago Press, Chicago, pp 161–196.
Divisia F (1926), ‘L’indice Monétaire et la Théorie de la Monnaie (Suite et Fin)’ (The Monetary Index and the Theory of Currency (Conclusion)), Revue d′Economie Politique, 40(1), pp 49–81.
European Commission, International Monetary Fund, Organisation for Economic Co-operation and Development, United Nations and the World Bank (2009), System of National Accounts, 2008, United Nations, New York.
Eurostat (2013), Handbook on Residential Property Price Indices (RPPIs), Methodologies and Working Papers, Under the joint responsibility of the International Labour Organization, International Monetary Fund, Organisation for Economic Co-operation and Development, Statistical Office of the European Union, United Nations Economic Commission for Europe and the World Bank, European Union, Luxembourg.
Feenstra RC (1994), ‘New Product Varieties and the Measurement of International Prices’, The American Economic Review, 84(1), pp 157–177.
Feenstra RC (1995), ‘Exact Hedonic Price Indexes’, The Review of Economics and Statistics, 77(4), pp 634–653.
Feenstra RC and J Romalis (2014), ‘International Prices and Endogenous Quality’, The Quarterly Journal of Economics, 129(2), pp 477–527.
Feenstra RC and MD Shapiro (2003), ‘High-Frequency Substitution and the Measurement of Price Indexes’, in RC Feenstra and MD Shapiro (eds), Scanner Data and Price Indexes, NBER Studies in Income and Wealth, Vol 64, University of Chicago Press, Chicago, pp 123–146.
Fisher I (1922), The Making of Index Numbers: A Study of Their Varieties, Tests, and Reliability, Publications of the Pollak Foundation for Economic Research, No 1, Houghton Mifflin Company, Boston.
Fodor J and M Roubens (1995), ‘On Meaningfulness of Means’, Journal of Computational and Applied Mathematics, 64(1–2), pp 103–115.
Fox KJ and IA Syed (2016), ‘Price Discounts and the Measurement of Inflation’, Journal of Econometrics, 191(2), pp 398–406.
Gábor-Tóth E and P Vermeulen (2017), ‘The Relative Importance of Taste Shocks and Price Movements in the Variation of Cost-of-Living: Evidence from Scanner Data’, Paper presented at the 15th Ottawa Group Meeting on Price Indices, Eltville am Rhein, 10–12 May.
Geary RC (1958), ‘A Note on the Comparison of Exchange Rates and Purchasing Power between Countries’, Journal of the Royal Statistical Society: Series A (General), 121(1), pp 97–99.
German Federal Statistical Office (Statistisches Bundesamt) (2003), ‘Hedonic Methods of Price Measurement for Used Cars’, Information paper, 20 October. Available at <https://www.destatis.de/EN/FactsFigures/NationalEconomyEnvironment/Prices/HedonicUsedCars.pdf%3F__blob%3DpublicationFile>.
Goldberger AS (1968), ‘The Interpretation and Estimation of Cobb-Douglas Functions’, Econometrica, 36(3/4), pp 464–472.
Griliches Z (1971), ‘Introduction: Hedonic Price Indexes Revisited’, in Z Griliches (ed), Price Indexes and Quality Change: Studies in New Methods of Measurement, Harvard University Press, Cambridge, pp 3–15.
Hajargasht G and DSP Rao (2010), ‘Stochastic Approach to Index Numbers for Multilateral Price Comparisons and Their Standard Errors’, The Review of Income and Wealth, 56(S1), pp S32–S58.
Hansen BE (2018), ‘Econometrics’, Unpublished manuscript, University of Wisconsin, rev January. Available at <https://www.ssc.wisc.edu/~bhansen/econometrics/Econometrics.pdf>.
Heravi S and M Silver (2007), ‘Different Approaches to Estimating Hedonic Indexes’, in ER Berndt and CR Hulten (eds), Hard-to-Measure Goods and Services: Essays in Honor of Zvi Griliches, NBER Studies in Income and Wealth, Vol 67, University of Chicago Press, Chicago, pp 235–268.
Hill RJ (1997), ‘A Taxonomy of Multilateral Methods for Making International Comparisons of Prices and Quantities’, The Review of Income and Wealth, 43(1), pp 49–69.
Hill RJ (2011), ‘Hedonic Price Indexes for Housing’, OECD Statistics Working Paper No 2011/01.
Iklé DM (1972), ‘A New Approach to the Index Number Problem’, The Quarterly Journal of Economics, 86(2), pp 188–211.
International Labour Office, International Monetary Fund, Organisation for Economic Co-operation and Development, Statistical Office of the European Communities, United Nations Economic Commission for Europe and the World Bank (2004), Consumer Price Index Manual: Theory and Practice, International Labour Office, Geneva.
International Labour Organization, International Monetary Fund, Organisation for Economic Co-operation and Development, United Nations Economic Commission for Europe and the World Bank (2004), Producer Price Index Manual: Theory and Practice, International Monetary Fund, Washington DC.
Ivancic L, WE Diewert and KJ Fox (2011), ‘Scanner Data, Time Aggregation and the Construction of Price Indexes’, Journal of Econometrics, 161(1), pp 24–35.
Jaimovich N, S Rebelo and A Wong (2015), ‘Trading Down and the Business Cycle’, NBER Working Paper No 21539, rev October 2017.
Jevons WS (1863), A Serious Fall in the Value of Gold Ascertained, and Its Social Effects Set Forth, Edward Stanford, London.
Jevons WS (1869), ‘Miscellanea: The Depreciation of Gold, 1847–69’, Journal of the Statistical Society of London, 32(4), pp 445–449.
Kennedy PE (1981), ‘Estimation with Correctly Interpreted Dummy Variables in Semilogarithmic Equations’, The American Economic Review, 71(4), p 801.
Keynes JM (1930), A Treatise on Money: Volume 1 The Pure Theory of Money, Macmillan and Co. Limited, London.
Khamis SH (1972), ‘A New System of Index Numbers for National and International Purposes’, Journal of the Royal Statistical Society: Series A (General), 135(1), pp 96–121.
Khandelwal A (2010), ‘The Long and Short (of) Quality Ladders’, The Review of Economic Studies, 77(4), pp 1450–1476.
Kloek T and GM de Wit (1961), ‘Best Linear and Best Linear Unbiased Index Numbers’, Econometrica, 29(4), pp 602–616.
Lloyd PJ (1975), ‘Substitution Effects and Biases in Nontrue Price Indices’, The American Economic Review, 65(3), pp 301–313.
Machado JA and JMC Santos Silva (2006), ‘A Note on Identification with Averaged Data’, Econometric Theory, 22(3), pp 537–541.
Montgomery JK (1937), The Mathematical Problem of the Price Index, P.S. King & Son, London.
Moulton B (2017), ‘The Measurement of Output, Prices, and Productivity: What's Changed since the Boskin Commission?’, Unpublished manuscript, November.
Nagumo M (1930), ‘Über eine Klasse der Mittelwerte’ (Over a Class of Means), Japanese Journal of Mathematics: Transactions and Abstracts, 7, pp 71–79.
National Research Council (2002), At What Price?: Conceptualizing and Measuring Cost-of-Living and Price Indexes, National Academy Press, Washington DC.
Office for National Statistics (2014), Consumer Price Indices Technical Manual: 2014 Edition, Office for National Statistics, Newport.
Pakes A (2003), ‘A Reconsideration of Hedonic Price Indexes with an Application to PC's’, The American Economic Review, 93(5), pp 1578–1596.
Persons WM (1928), ‘The Effect of Correlation between Weights and Relatives in the Construction of Index Numbers’, The Review of Economics and Statistics, 10(2), pp 80–107.
Rao DSP (1990), ‘A System of Log-Change Index Numbers for Multilateral Comparisons’, in J Salazar-Carrillo and DSP Rao (eds), Comparisons of Prices and Real Products in Latin America, Contributions to Economic Analysis, Vol 194, Elsevier Science Publishers B.V., Amsterdam, pp 127–139.
Rao DSP and G Hajargasht (2016), ‘Stochastic Approach to Computation of Purchasing Power Parities in the International Comparison Program (ICP)’, Journal of Econometrics, 191(2), pp 414–425.
Redding SJ and DE Weinstein (2018), ‘Measuring Aggregate Price Indexes with Demand Shocks: Theory and Evidence for CES Preferences’, NBER Working Paper No 22479, rev May.
Rosen S (1974), ‘Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition’, Journal of Political Economy, 82(1), pp 34–55.
Sato K (1974), ‘Ideal Index Numbers that Almost Satisfy the Factor Reversal Test’, The Review of Economics and Statistics, 56(4), pp 549–552.
Sato K (1976), ‘The Ideal Log-Change Index Number’, The Review of Economics and Statistics, 58(2), pp 223–228.
Selvanathan E and DSP Rao (1994), Index Numbers: A Stochastic Approach, The Macmillan Press Ltd, London.
Solon G, SJ Haider and JM Wooldridge (2015), ‘What Are We Weighting For?’, The Journal of Human Resources, 50(2), pp 301–316.
Stoevska V (2008), ‘Consumer Price Index Manual: Theory and Practice – Report on the 2007 Worldwide Survey on the Usefulness of the CPI Manual’, Report, International Labour Organization. Available at <http://www.ilo.org/public/english/bureau/stat/download/cpi/survey.pdf>.
Stuvel G (1957), ‘A New Index Number Formula’, Econometrica, 25(1), pp 123–131.
Syed I, RJ Hill and D Melser (2008), ‘Flexible Spatial and Temporal Hedonic Price Indexes for Housing in the Presence of Missing Data’, University of New South Wales, School of Economics Discussion Paper 08–14. Available at <https://ideas.repec.org/p/swe/wpaper/2008–14.html>.
Theil H (1960), ‘Best Linear Index Numbers of Prices and Quantities’, Econometrica, 28(2), pp 464–480.
Theil H (1967), Economics and Information Theory, Studies in Mathematical and Managerial Economics, Vol 7, North Holland Publishing Company, Amsterdam.
Törnqvist L (1936), ‘The Bank of Finland's Consumption Price Index’, Bank of Finland Monthly Bulletin, 16(10), pp 27–34.
Triplett J (2004), Handbook on Hedonic Indexes and Quality Adjustments in Price Indexes: Special Application to Information Technology Products, OECD Publishing, Paris.
Ueda K, K Watanabe and T Watanabe (2016), ‘Product Turnover and Deflation: Evidence from Japan’, Australian National University, Crawford School of Public Policy, Centre for Applied Macroeconomics Analysis, CAMA Working Paper 71/2016.
Vartia YO (1976), ‘Ideal Log-Change Index Numbers’, Scandinavian Journal of Statistics, 3(3), pp 121–126.
Voltaire K and EJ Stack (1980), ‘A Divisia Version of the Country-Product-Dummy Method’, Economics Letters, 5(1), pp 97–99.
von Auer L (2014), ‘The Generalized Unit Value Index Family’, The Review of Income and Wealth, 60(4), pp 843–861.
Walsh CM (1901), The Measurement of General Exchange-Value, The Macmillan Company, New York.
Wooldridge JM (2010), Econometric Analysis of Cross Section and Panel Data, 2nd edn, MIT Press, Cambridge.
World Bank (2013), Measuring the Real Size of the World Economy: The Framework, Methodology, and Results of the International Comparison Program—ICP, World Bank, Washington DC.
Acknowledgements
For their input I thank Bert Balk, Anthony Brassil, Jan de Haan, Michele De Nadai, Denzil Fiebig, Kevin Fox, SeoJeong (Jay) Lee, Alicia Rambaldi, John Simon, Franklin Soriano, and participants at several seminars and conferences. Rosie Wisbey sourced some elusive materials. This work forms part of my PhD at the University of New South Wales and was supported by an Australian Government Research Training Scholarship. The views expressed in this paper are those of the author and do not reflect those of the Reserve Bank of Australia. Any errors are my own.
Footnotes
For another application the 2008 System of National Accounts does list some relevant cases in which gauging quality like this is not ideal (European Commission et al 2009, p 303). [1]
The superpopulation viewpoint can encompass the finite population one, by conceptualising the population outcomes as having discrete possibilities, with densities proportional to realised incidence. [2]