RDP 2017-02: Anticipatory Monetary Policy and the ‘Price Puzzle’ 5. Large-scale Structural Econometric Models
May 2017
The price puzzle found in VARs contrasts with the results from large-scale structural econometric models, the approach that VARs were designed to replace. In Figure 10 we show estimates from two large-scale models of the Australian economy: the AUS-M model of Outlook Economics and the Global Economic Model of Oxford Economics. The orange lines trace out the effect on the quarterly inflation rate of a 1 percentage point increase in the cash rate, for one quarter, after which interest rates are endogenous (an experiment that facilitates comparisons with VARs). The blue lines show the effect of a 1 percentage point increase in the cash rate for four quarters, after which it responds endogenously (a more common experiment with these kinds of models).
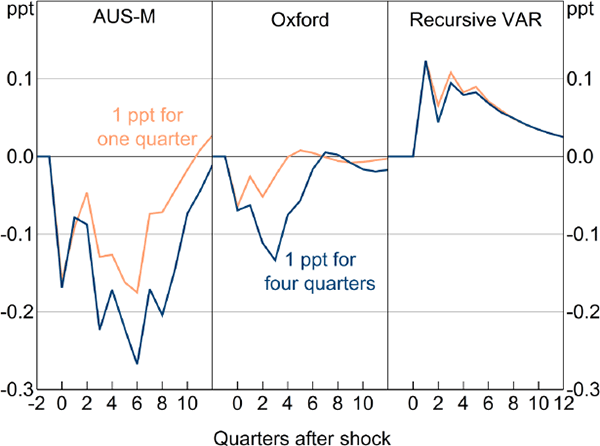
Notes: Inflation is based on the headline consumer price index in the AUS-M and Oxford Economics' Global Economic Model, and the trimmed mean measure for the recursive VAR
Sources: ABS; Authors' calculations; Outlook Economics; Oxford Economics
In contrast to the results presented earlier, the large-scale models estimate that inflation and the price level will fall in response to an interest rate increase (Figure 10). This result is in line with that of large-scale models of the US economy, such as the FRB/US model (Reifschneider, Tetlow and Williams 1999, p 8) and the Fairmodel (Fair 2013, p 180).
A precise decomposition of why the large-scale models give the opposite result to VARs would be complicated. But at the risk of over-generalising, the large-scale models appear to have larger Phillips curve and exchange rate effects than shown in Figure 2. That may reflect the exclusion of wages and the unemployment rate from VARs. It may also reflect the shorter sample period of the VAR. However, a large part of the difference seems to be that interest rates are excluded by assumption from the inflation equation in the large-scale models, but not in VARs. This reflects methodological differences discussed below.
Estrella (2015) highlights the importance of the restrictions on lagged effects of interest rates in reduced-form equations for inflation. Using US data and an otherwise standard structural VAR, Estrella finds that excluding the first lag of the federal funds rate eliminates the price puzzle. He argues this restriction can be motivated by the ‘well-established stylized fact’ that monetary policy operates with long lags. He also presents a simple theoretical model – one without any direct channel from the lagged interest rate to inflation – consistent with this restriction.
The structural VAR developed for Australia by Dungey and Pagan (2000, 2009) also omits interest rates from the inflation equation. It is noteworthy therefore that this model does not exhibit a price puzzle. However, Dungey and Pagan's specification differs from a ‘standard’ structural VAR for reasons other than this restriction; for example, it is a large (11-variable) model that imposes a range of theoretically-motivated restrictions on contemporaneous and lagged effects.
In a more parsimonious VAR such as the one used in Section 1.1, excluding lags of interest rates from the inflation equation is not sufficient to eliminate the price puzzle; although the price puzzle is smaller than the model that does not impose this constraint and is no longer statistically significant. This is true whether we omit the first lag of the cash rate or all three lags from the reduced-form inflation equation.[15] Thus, although the presence of lagged interest rates in the inflation equation is likely to exacerbate the price puzzle, excluding this variable from the model is unlikely to be a panacea.
The above discussion raises important methodological issues. Plausible estimates of the effect of interest rates on inflation seem to come from modelling approaches that involve detailed inspection and respecification of individual equations. This often involves imposition of zero restrictions when estimated coefficients are insignificant or inconsistent with theory or other information. This is standard practice in large-scale models, but can also be done in a VAR (e.g. Dungey and Pagan 2000, 2009). However, these issues are controversial. Equation-by-equation respecification seems to be inconsistent with the rationale for VARs originally proposed by Sims (1980), who argued for common specification across equations.
Footnotes
At first glance, the results in Figure 2 seem to imply that if we omit lagged interest rates from the inflation equation that the price puzzle will completely disappear. However, in Figure 2 this restriction was imposed after estimation, holding other coefficients constant. The other coefficients in the inflation equation will change if interest rates are excluded, picking up some of their correlation. [15]