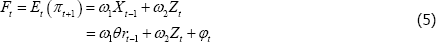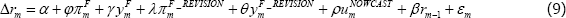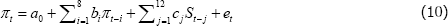Research Discussion Paper – RDP 2017-02 Anticipatory Monetary Policy and the ‘Price Puzzle’
Introduction
Vector autoregressions (VARs) often find that inflation increases in response to a tightening in monetary policy, although mainstream macroeconomics predicts the opposite. This ‘price puzzle’ is commonly thought to reflect interest rates being tightened in anticipation of future inflation, reflecting information possessed by policymakers beyond that contained in the model. An influential paper by Romer and Romer (2004) successfully removes the price puzzle from US data by purging the policy interest rate of any systematic responses to central bank forecasts. Cloyne and Hürtgen (2016) also use this approach to eliminate the price puzzle for the United Kingdom. We apply the same approach to Australian data and find that our estimation fails to remove the price puzzle. Under a wide range of specifications, higher interest rates are estimated to lead to higher inflation. These results are difficult to explain. We think this raises important questions about the reliability of VARs for the analysis of monetary policy.
1.1 Documenting the Price Puzzle
We begin with an Australian illustration of the price puzzle. We estimate a recursive VAR that is similar, in terms of variables and lag structure, to models used in previous Reserve Bank research (Brischetto and Voss 1999; Berkelmans 2005; Lawson and Rees 2008; Jääskelä and Jennings 2010; Jacobs and Rayner 2012). Variables include: US real GDP, commodity prices, real GDP, underlying inflation, the cash rate, and the real exchange rate (real TWI), in that order. Appendix A provides further details about the variables and model specification.
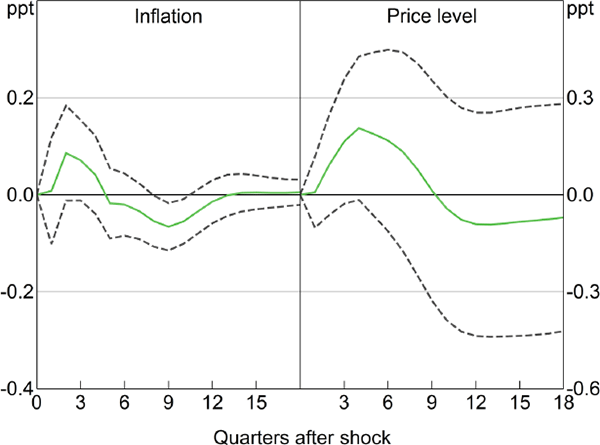
Figure 1 shows the responses of real GDP, underlying inflation and the price level (i.e. the cumulated response of inflation) to a 1 percentage point shock to the cash rate. Output declines, as would be expected. However, inflation responds perversely, rising by 0.1 percentage point (at a quarterly rate) one quarter after the shock and remaining there for the next year or so. The price level is permanently higher. This is known as the price puzzle. All responses are statistically significant at a 10 per cent level, with the 90 per cent confidence intervals calculated by repeated resampling from the asymptotic distribution of the parameters (1,000 times).
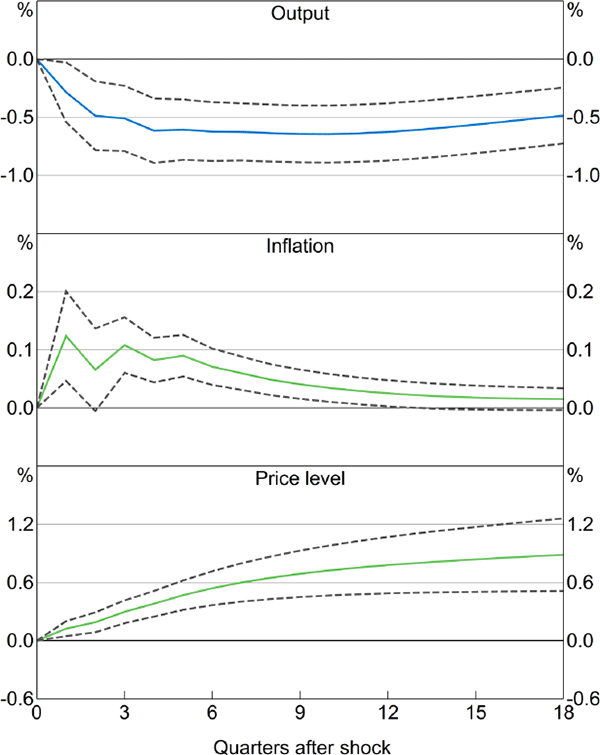
Notes: Price level is the cumulated response of underlying inflation to the monetary policy shock; confidence bands indicate 90 per cent intervals; sample period is 1990:Q2–2015:Q4
Sources: ABS; Authors' calculations
Results like these are common in the international literature. In a survey of 70 studies using VARs spanning 31 countries, Rusnak, Havranek and Horvath (2013) found that half showed a price puzzle. They note that this likely understates the pervasiveness of the result, since studies finding a price puzzle are less likely to get published in academic journals. Examples of price puzzles in Australian VARs include Phan (2014, p 387), Beechey and Österholm (2008, p 455) and, arguably, Suzuki (2004, p 150). Several of the RBA papers cited above also show price puzzles, which is unsurprising, given that the specifications are often similar to the one used in Figure 1.
The price puzzle is generally thought to reflect central banks setting monetary policy in a forward-looking way, using information beyond that contained in the VAR. For example, if the central bank correctly anticipates an imminent increase in inflation, following a pick-up in leading indicators, its pre-emptive rate rise will be followed by a period of higher inflation, leading the VAR to attribute that inflation to the rate rise. Similar logic also implies that the estimated response of output will be biased towards zero due to anticipatory policy.
Support for this interpretation comes from a decomposition of the price puzzle. Figure 2 decomposes the inflation response from Figure 1 into the direct effects of interest rates on inflation (blue bars), along with the indirect effects operating through the Phillips curve (maroon bars) and exchange rate (pink bars).[1] These contributions are calculated by setting relevant coefficients in the inflation equation equal to zero, after estimation. For example, the ‘direct effect’ of interest rates is the difference between the overall inflation response and the response when the coefficients on the cash rate in the inflation equation are set to zero. Similarly, the ‘Phillips curve’ and ‘exchange rate’ contributions are the difference between the overall response and the response once we set to zero the coefficients on real GDP and the real TWI, respectively. The components do not sum to the total because of interaction effects (grey bars). Figure 2 shows that the price puzzle in a recursive VAR does not arise because of problems estimating the Phillips curve or exchange rate channels of monetary policy, since these channels exert a deflationary influence. Rather, the price puzzle stems from the coefficients on the policy interest rate in the inflation equation. These coefficients are large, statistically significant and ‘incorrectly’ signed. The effect essentially occurs with a one-quarter lag, which rules out interpretations implying delayed or gradual responses.
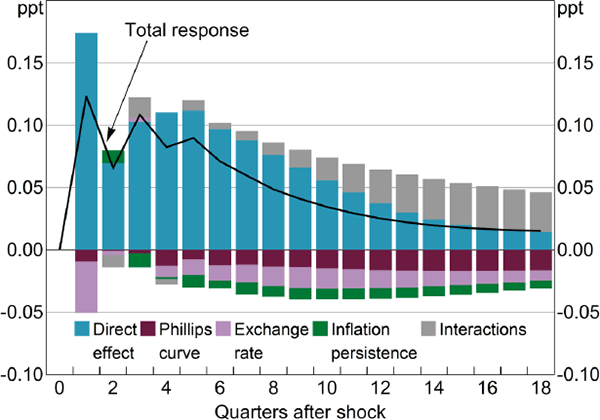
Notes: Total response of underlying inflation to a 1 percentage point contractionary monetary policy shock, as in middle panel of Figure 1; sample period is 1990:Q2–2015:Q4
Sources: ABS; Authors' calculations
An implication of Figure 2 is that it is not necessary to estimate a VAR or other system to generate a price puzzle. It arises from estimating a single equation. The recursive inflation equation, by itself, implies that an increase in the cash rate of 1 percentage point increases inflation by 0.18 percentage points in the following quarter (with a standard error of 0.064), holding other variables constant.[2] The other variables and equations in the VAR add some momentum, but do not change the character of the response.
To see more clearly how anticipatory monetary policy can generate a price puzzle, assume that the ‘true model’ of inflation takes the following form,
where πt is the inflation rate in period t, rt is the cash rate announced in period t, Xt − 1 is a determinant of inflation observed by the econometrician (e.g. the exchange rate or the unemployment rate), Zt − 1 is another variable that helps the central bank predict inflation (e.g. oil prices or wages), and εt and et are error terms. For simplicity, assume that the transmission from the cash rate to inflation occurs through X but not Z.
The key parameter of interest is βθ, which measures the effect on inflation next period due to a unit change in the cash rate this period. However, rather than estimating Equations (1) and (2), the econometrician estimates a reduced-form equation that incorrectly omits the Zt − 1 variable,
where νt ≡ γZt−1 +
(εt+βet−1) is a composite
error term. The least squares estimator 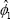 will be
will be
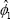 will be a
biased estimator of the true effect of policy on inflation, βθ, if both of
the following hold:
will be a
biased estimator of the true effect of policy on inflation, βθ, if both of
the following hold:
- cov(rt−1,Zt−1) ≠ 0. Policy responds to a wider range of inflation indicators than those included in the VAR.
- γ ≠ 0. These variables have additional predictive power for future inflation.
As can be seen from the discussion of the outlook presented in the Statement on Monetary Policy, the RBA's inflation forecasts are informed by a wider range of indicators than appear in VARs. For example, liaison with resource firms provided the Bank with ‘quite accurate information about the timing and magnitude of the downturn in mining investment that significantly improved our forecasts’ (Heath 2015). A priori, it is unclear whether the forecasts have explanatory power for future inflation above and beyond that contained in a VAR, although the finding that RBA forecasts of inflation have been more accurate than alternative forecasts suggests that this is likely (Tulip and Wallace 2012, Section 4.3).
The sign of the bias is likely to be positive if the above conditions hold and if interest rates respond positively to the inflation outlook, which is the typical response for an inflation-targeting central bank such as the RBA. In Section 2.1, we provide empirical evidence that the RBA responds in this way to the inflation forecast. This bias is the most common explanation put forward for the existence of the price puzzle.
A positive effect of interest rates on inflation is generally regarded as implausible, although there are some exceptions to the consensus, which we discuss in Section 4. In particular, this result appears to be inconsistent with the largest (and hence the easiest to interpret) movements in the data. Periods of unusually tight monetary policy, such as in Australia in 1989–90, the United States in 1979–82 or the United Kingdom in 1979–82, were followed by declining output, then large falls in inflation. These episodes convinced many observers that monetary policy has a strong effect on inflation. A second reason is that the price puzzle seems to be inconsistent with the stationarity of interest rates and inflation. Central banks say they respond to accelerating inflation by raising nominal interest rates. But if inflation responded positively to changes in interest rates, tighter policy would amplify the inflation, resulting in instability of nominal interest rates and inflation. However, interest rates and inflation have been stable, especially under the current policy of inflation targeting. Finally, mainstream macroeconomic theories and textbooks (e.g. Woodford 2003; Galí 2008; Mankiw 2015) imply higher interest rates would lower inflation.
Following Sims (1992), it has been common to control for commodity prices in VARs. An increase in commodity prices often leads to increases in both inflation and interest rates and hence gives rise to a positive correlation between these variables. That is, commodity prices are an important element of Z in Equation (1). However, the responses shown in Figure 1 come from a VAR that already includes commodity prices, and we measure inflation with the trimmed mean, on which commodity prices have little direct effect. Approximately half the estimates in the survey by Rusnak et al (2013) allow for commodity prices, and of these, half still report a price puzzle. This may reflect sensitivity of the results to the precise measure of commodity prices, and in particular, whether they include oil prices. Or, more likely, it may be that commodity prices are just one component of the inflation forecast and hence do not fully control for forward-looking policy.
Another approach to the price puzzle has been to estimate a factor-augmented VAR (FAVAR), where a large number of possibly relevant macroeconomic and financial series are summarised by principle components. Bernanke, Boivin and Eliasz (2005) show that a FAVAR removes the price puzzle from US data. On a conceptual level, FAVARs are similar to controlling for central bank forecasts, in that they summarise and apply a wide range of data. However, FAVARs have greater data requirements and are harder to interpret. On a practical level, including the first and second principal components from Gerard and Nimark (2008) in the VAR in Section 1 fails to remove the price puzzle (for results, see Appendix B).
The remainder of the paper proceeds as follows. In Section 2, we discuss Romer and Romer's (2004) approach to addressing the price puzzle along with the methodology used in our paper and our baseline estimates. Section 3 examines the robustness of our baseline estimates to using alternative specifications and data. Section 4 provides some interpretations of our results. Section 5 contrasts our findings with those from large-scale structural econometric models. Section 6 offers some concluding remarks.
2. Romer and Romer's Approach
Romer and Romer (2004) argue that central bank forecasts should reflect all relevant information about the outlook.[3] To remove the anticipatory component of policy, Romer and Romer use the Federal Reserve's internal forecasts for output and inflation. This approach involves two steps:
- First, purge the cash rate series of anticipatory policy changes. This involves regressing changes in the cash rate on the forecasts for inflation and output growth. The estimated residuals from this regression become the measure of ‘monetary policy shocks’.
- Use the measure of monetary policy shocks derived in Step 1 to estimate the effect of a change in policy on output and inflation. We can do this in a single-equation framework or in a VAR.
To see how this approach can remove the effect of anticipatory policy, assume that the central bank's inflation forecasts, Ft, place weight on both X and Z variables. Assume for now that the forecasts are compiled under the assumption of no change in the policy interest rate. This assumption, which we discuss further below, means there is no feedback from policy to the forecast. One way to incorporate this assumption into our analytical framework is to assume that X enters the forecast with a lag,
where φt = ω1et−1. Thus, dEt (πt+1)/drt = 0.
The first stage of the Romer and Romer procedure is to estimate the central bank's reaction to the forecasts, which in simplified form can be written as
where the least squares residuals, 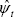 , represent a ‘shock’
to the policy interest rate.[4]
This shock is any deviation from the usual relationship between interest rates and the forecast
for inflation. The second stage of Romer and Romer involves estimating
, represent a ‘shock’
to the policy interest rate.[4]
This shock is any deviation from the usual relationship between interest rates and the forecast
for inflation. The second stage of Romer and Romer involves estimating
The estimator of κ1 in the second-stage regression is
The Romer and Romer two-step estimator is unbiased 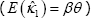 , even though the
econometrician does not directly observe Z, because the interest rate shocks are
constructed so as to be orthogonal to the central bank's information set
, even though the
econometrician does not directly observe Z, because the interest rate shocks are
constructed so as to be orthogonal to the central bank's information set 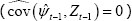 .[5]
.[5]
The following two sections discuss how we apply the Romers' two steps to Australian data.[6]
2.1 Step #1: Construct the Measure of Monetary Shocks
The Board of the RBA meet to decide on the target cash rate 11 times per year, on the first Tuesday of every month except January. At four of these meetings – February, May, August and November – economic forecasts are considered and then published a few days later in the Statement of Monetary Policy (SMP). Before the publication of inflation forecasts began in 2000, forecasts were prepared for the Joint Economic Forecasting Group (JEFG), held in March, June, September and December. For our baseline results, we restrict attention to interest rate decisions when an inflation forecast was first available, which we refer to as ‘forecast months’. These are end-quarter months prior to 2000 and mid-quarter months after 2000. Forecasts are taken from Tulip and Wallace (2012), which we have updated.
Using data for forecast months, we estimate the following first-stage regression, in a specification that follows Romer and Romer (2004) with a few small modifications:
That is, we regress the change in the target cash rate announced at Board meeting m on
the two-quarter-ahead forecasts of year-ended underlying inflation 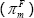 and real GDP growth
and real GDP growth 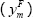 , along with the revisions to the forecasts
since the previous forecast round three months ago
, along with the revisions to the forecasts
since the previous forecast round three months ago 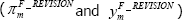 .[7] We also include
the Bank's nowcast of the unemployment rate
.[7] We also include
the Bank's nowcast of the unemployment rate 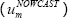 for the current
quarter (which incorporates some real-time data) and the cash rate announced at the previous
month's Board meeting (rm − 1).
for the current
quarter (which incorporates some real-time data) and the cash rate announced at the previous
month's Board meeting (rm − 1).
This specification deviates slightly from the first-stage expression described in Section 2 in that it controls for more than just the forecast for inflation; it also includes output forecasts, the unemployment rate and a lag of the cash rate. We discuss this issue and other possible variations in Section 3.
Our main departure from Romer and Romer (2004) is that we specify the forecasts in terms of year-ended percentage changes, rather than including the separate one- and two-quarter-ahead forecasts of quarterly inflation (and GDP growth), real-time data for the previous quarter and nowcasts for the current quarter. We do this partly to preserve degrees of freedom given our smaller sample size of interest rate decisions relative to Romer and Romer. (In the United States, forecasts and data are more frequent and are available for a much longer period of history). It does not seem plausible that policy would react very differently to forecasts in adjacent quarters and using year-ended forecasts is equivalent to constraining coefficients at different horizons to be equal. Estimating from 2001, this restriction is not strongly rejected (p = 0.09).[8]
Our sample covers 100 Board meetings since 1991 (when the Tulip and Wallace (2012) dataset begins). Cash rate changes at these meetings account for 37 per cent of all announced changes, in absolute terms, in the cash rate. Our sample primarily spans the inflation-targeting period but also captures the early 1990s recession and disinflation. Our sample period also happens to roughly coincide with the period during which the RBA has announced targets for the cash rate, which commenced in 1990.
One potential issue with our baseline specification is that SMP forecasts are finalised after Board decisions are announced and thus incorporate financial market and other reactions to the announcement. This differs from the assumption made in Section 2 that the forecasts do not embody the current month's policy decision. This feedback makes analytical properties (such as our discussion of unbiasedness) complicated. However, Board decisions and market reactions to them usually have little effect on forecasts at the short forecast horizons we consider. This can be seen in Figure 3, which plots the Bank's official two-quarter-ahead inflation forecasts published several days after the Board meeting (y-axis) against the forecasts that were presented to the Board (x-axis).[9] The latter are taken from the Bank's unpublished forecast archives and are only available from May 2001 onwards. The figure distinguishes between meetings where the cash rate was decreased (blue dots), increased (red dots) or left unchanged (orange dots). There is little evidence of feedback from the policy decision to the forecast. Although a handful of blue dots lie above the 45 degree line and a single red dot lies below the 45 degree line – suggesting a feedback effect – the magnitudes are trivial.[10] The size of these feedback effects is likely to be much larger if we consider longer-run forecasts.
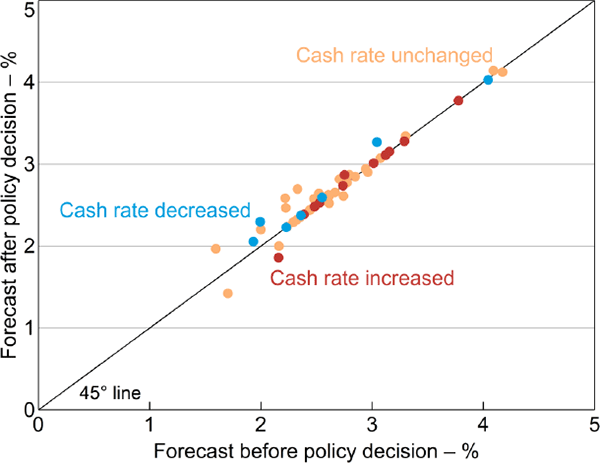
Notes: Forecasts before the policy decision are those presented to the Board or to the internal Policy Discussion Group; forecasts after the policy decision are those published in the SMP following the Board meeting; sample is forecast-meeting months from May 2001 to February 2015
Source: RBA
In Section 3 we consider some alternative specifications that make different timing assumptions about the forecasts. Robustness of our results to these variations supports our assessment that precise timing of the forecast does not matter much.
Concerns about potential feedback effects from the current month's policy decision – and the future path of policy rates – motivate us to use forecasts at fairly short horizons. Moreover, as Romer and Romer (2004) point out, both inflation and output growth are serially correlated enough that forecasts one and two quarters ahead provide a good indication of the likely forecasted path of the economy over longer horizons. Our decision to focus on short-horizon forecasts is also pragmatic, in that data on forecasts at longer horizons are often unavailable, particularly in the early part of our sample.
The results from estimating Equation (9) are presented in Table B1. The coefficients summarising the outlook for inflation (both the level of the forecast and the revision relative to the previous forecasting round) are jointly significant, with a p-value below 1 per cent. The Board reacts mainly to revisions to the inflation outlook. The sum of the two inflation terms is 0.19, such that a 1 percentage point increase in the two-quarter-ahead forecast for year-ended inflation leads to a 19 basis point increase in the cash rate. The small size of this response – which appears to imply that real interest rates decline in response to positive inflation surprises – is qualitatively similar (and in between) the estimates of Romer and Romer (2004) for the United States and Cloyne and Hürtgen (2016) for the United Kingdom. The coefficients on the output forecasts are positive but not statistically significant. Summing the two coefficients suggests that a 1 percentage point upgrade to the GDP growth forecast is associated with an increase in the cash rate of 6 basis points. The insignificance of the output forecasts may reflect that there is not enough independent variation in the output and inflation forecasts to disentangle their separate contributions.[11]
The estimates suggest that the RBA clearly reacts to forecasts of inflation. As noted earlier, coupled with the substantial correlation between forecasts and future developments, this forward-looking behaviour implies a bias in estimates of the effects of policy on inflation in standard VAR models.
The top panel of Figure 4 shows the actual changes in the cash rate announced immediately after forecast-month Board meetings, along with the fitted values from Equation (9). The bottom panel of Figure 4 plots the residuals – our measure of monetary shocks. Some of the largest policy shocks occurred during the 2008–09 downturn, when the RBA cut the cash rate by more than historical relationships would suggest, given the forecasts for output and inflation generated at the time. In contrast, there were large contractionary shocks between August and December 1994, with the size of the monetary policy tightening appearing unusually large. As emphasised by Stevens (1999), this tightening cycle occurred at a time when the RBA had recently adopted inflation targeting and inflation expectations remained weakly anchored. In such an environment, a more aggressive response to anticipated inflation may be required to prevent the pick-up in inflation from occurring, as well as to reinforce credibility of the central bank's policy regime.
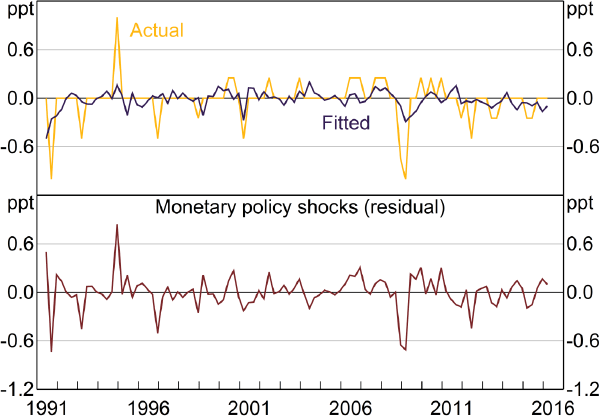
Sources: ABS; Authors' calculations
To be clear, Equation (9) is not intended as a full description of the Board's behaviour and we do not attempt to maximise its R2. In particular, we intentionally do not control for other variables that the Board may consider when setting policy, such as the exchange rate and housing prices. It is possible that the Board responds to these variables above and beyond their direct impact on the forecasts for inflation and output. From the perspective of estimation, this would be desirable, since changes in the cash rate in response to variables such as housing prices provide us with the variation we require to estimate the effects of monetary policy on inflation and output.
2.2 Step #2: Effect of a Monetary Shock on Inflation and Output
2.2.1 Single-equation estimation
The simplest way to estimate the effect of a monetary policy shock on inflation is to regress the quarterly inflation rate on a constant, its own lagged values, and lagged values of our series of monetary policy shocks (an autoregressive distributed lag (ADL) model).
where πt is trimmed mean inflation (measured in quarterly log differences, multiplied by 100) and St is our new measure of monetary shocks. We have assigned each policy shock to the quarter in which it occurs; for example, the estimated shock at the November 2008 Board meeting is the policy shock for 2008:Q4.
We can validly estimate using a single bivariate equation because we have already removed the effect of other influences on inflation through the forecast. This is in contrast to VAR identification strategies, in which the monetary shock is identified within the VAR itself. Following the literature, we assume that monetary policy does not affect inflation contemporaneously. This assumption does not affect our results. We include 8 lags of inflation and 12 lags of the monetary shock measure.[12]
2.2.2 The inflation response
We first show a simple version of the price puzzle using an ADL model as a basis for comparison. The left panel of Figure 5 shows the dynamic response of the price level – that is, the cumulated response of quarterly inflation – to a 1 percentage point increase in interest rates. This is based on a version of Equation (9), in which we use changes in the cash rate announced at forecast-month Board meetings instead of our shock series. We find a price puzzle similar to those shown in Section 1.
The right panel of Figure 5 repeats this exercise using Equation (9). This differs from the left panel in that interest rate changes are purged of forward-looking behaviour using RBA forecasts. A contractionary shock to monetary policy is still estimated to have a positive and statistically significant effect on inflation and the price level. Purging the cash rate series of responses to the forecasts does not reduce the size of the price puzzle. This is the central result of our paper.
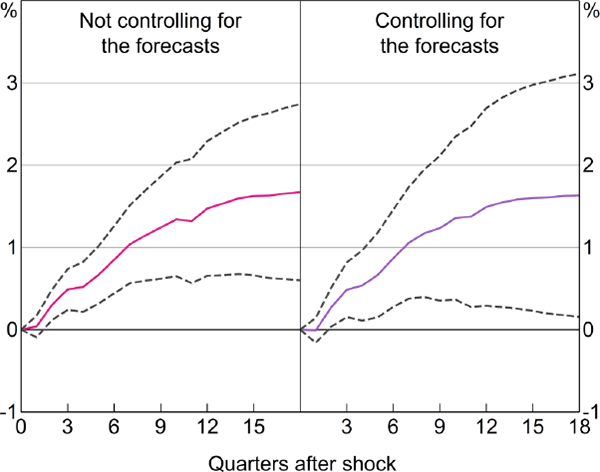
Notes: ADL model; shows the cumulated response of the price level to a permanent 1 percentage point shock to the cash rate; confidence bands indicate 90 per cent intervals; sample period is 1994:Q2–2015:Q4
Sources: ABS; Authors' calculations
These results are surprising in several respects. The approach used to estimate Figure 5 is essentially the same as that of Romer and Romer (2004) and Cloyne and Hürtgen (2016). They find that purging policy of systematic responses to the forecast eliminates the price puzzle in the United States and United Kingdom, respectively. We do not see any obvious reason why results for Australia should be different. There are some differences in the nature of our data relative to that in the United States and United Kingdom, but sensitivity analysis in Section 3 does not indicate these differences are important. Conceptually, anticipatory policy is the obvious and standard explanation for the price puzzle and it is difficult to see how controlling for central bank forecasts would not remove this. We discuss these puzzles and some suggested solutions in Section 4.
The statistical significance of the price puzzle is also noteworthy, and has implications for the specification of our baseline. It implies that there is enough variation in our measure of policy shocks to permit confident inference. Were this not the case, there would be an argument for broadening our baseline measure of policy shocks to include other changes in interest rates, such as from months without recently updated forecasts or before the 1990s. We exclude these cash rate changes from our baseline – paying a cost in efficiency – because it is harder to confidently purge them of forward-looking behaviour. Nevertheless, as we show in Section 3, including these cash rate variations does not change our central results.
2.2.3 The output response
Given the implausible nature of our estimates for inflation, it is not clear what weight should be placed on our results for the effect of monetary policy on output. If we have failed to plausibly estimate the effect of monetary policy on inflation, it is hard to see how we can assume that the same approach and shock series will yield reliable estimates for the response of output. Nevertheless, policy multipliers for output are the focus of much of the literature. To estimate the impact of monetary shocks on output we simply replace the inflation terms in Equation (9) with quarterly real GDP growth. The left panel of Figure 6 shows the effect of a change in interest rates on real GDP. The right panel shows the effect of our shock series. Purging the interest rate series of anticipatory policy makes little difference to the results, again in contrast to the results of Romer and Romer (2004) and Cloyne and Hürtgen (2016) who find a larger effect on output when adjusting for anticipatory policy.
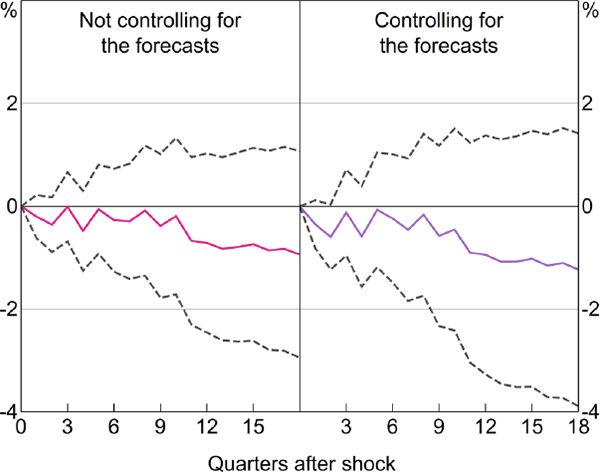
Notes: ADL model; confidence bands indicate 90 per cent intervals; sample period is 1994:Q2–2015:Q4
Sources: ABS; Authors' calculations
3. Robustness to Alternative Specifications
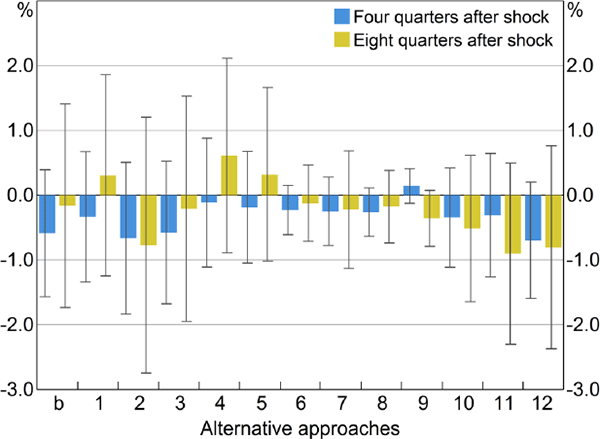
Because our baseline results for inflation were so surprising, we experimented with alternative specifications of the first-stage regression. We present 12 of these alternatives, together with our baseline labelled ‘b’, in Figure 7. These alternatives are briefly described below with further details where necessary in Appendix C. For the baseline and each of the 12 different specifications, the blue columns show estimated responses of the price level after four quarters to a 1 percentage point contractionary shock to monetary policy. Olive columns show responses after eight quarters and black lines show 90 per cent confidence intervals.
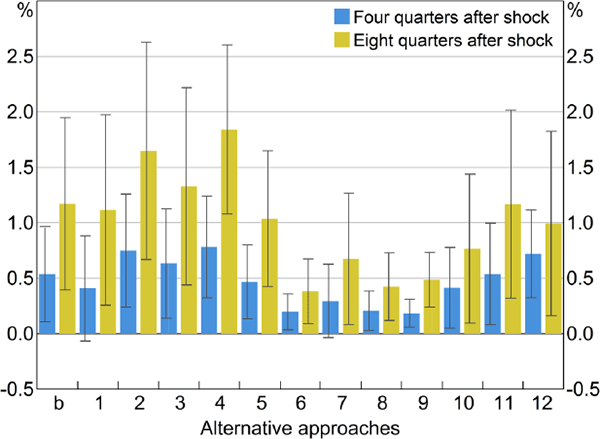
Notes: ADL model; blue bars show the cumulated response of inflation four quarters after a permanent 1 percentage point shock to the cash rate, using the 12 alternative approaches for constructing the cash rate shock; olive bars show the response after eight quarters, and black lines are 90 per cent confidence intervals; sample period for most estimates is 1994:Q2–2015:Q4, exceptions are: Approach 4, which begins in 1996; Approach 7, which begins in 2001; Approach 8, which begins in 1990; and Approach 9 which begins in 1988:Q3
Sources: ABS; Authors' calculations; Business Review Weekly; Consensus Economics; RBA
As explained earlier, our baseline only includes forecasts with a horizon out to two quarters ahead. Forecasts at longer horizons are more likely to be contaminated by the current month's policy decision and the assumed path of the cash rate going forward. However, policymakers often explain their decisions with reference to a longer-term outlook. Accordingly, our first alternative specification replaces the two-quarter-ahead forecasts for year-ended GDP growth and inflation in Equation (9) with four-quarter-ahead forecasts. Estimates are shown as Approach 1 in Figure 7.
In Approach 2 we replace the GDP forecasts with forecasts for the unemployment rate, which some argue are more relevant to the inflation outlook than the GDP growth forecasts. Extending the unemployment rate and inflation forecasts out to four quarters ahead (as in Approach 1) also gave similar results (not shown).
In Approach 3 we include the change in the cash rate announced at the previous month's Board meeting in the first-stage regression in order to allay concerns about serial correlation, interest rate smoothing or the omission of a persistent variable. In some estimated Taylor rules, this variable is highly significant.
As noted earlier, in the early and mid 1990s the Bank responded more aggressively than usual to the inflation outlook in order to reinforce credibility in the inflation target. Barakchian and Crowe (2013) argue that such changes in the weight on the forecasts in the central bank's reaction function could lead to misleading results. In Approach 4, we restrict our sample to begin in 1996:Q1, a period for which the coefficients on the policy rule were arguably more stable. The resulting series should identify a narrower set of monetary shocks, namely innovations to the policy rule rather than changes in the coefficients of the rule.
In Section 2 we showed that an unbiased estimate of the effect of the cash rate on inflation can be obtained by controlling for central bank inflation forecasts, and nothing else. Cochrane (2004) argues that this is more efficient than Romer and Romer's (2004) approach, since it purges policy of systematic anticipatory changes while retaining all other variations in the cash rate – including any responses to activity above and beyond its effect on the inflation outlook – to estimate the effect on inflation more precisely. Consistent with this argument, we control only for the inflation forecasts out to four quarters ahead in Approach 5.[13] Cochrane argues this ‘stripped down’ model is asymptotically equivalent to Romer and Romer's estimator (i.e. our baseline model). However, in small samples the approaches can and do yield different results.
We do not adopt Approach 5 as our baseline, preferring the approach of Romer and Romer (2004) and Cloyne and Hürtgen (2016), who also control for estimates of output growth and the unemployment rate. A rationale is that policymakers may react to inflation at longer horizons than included in our regression, or focus on alternative measures of inflation. If so, key determinants of inflation, such as the extra controls, may capture some anticipatory behaviour. This arguably reduces misspecification bias at a cost of some efficiency.
Approaches 1–5 follow the baseline in constructing shocks by using cash rate changes from forecast-month meetings. This omits 7 out of every 11 Board meetings each year, which reduces the variation in the cash rate and hence impairs the efficiency of our estimator. The rationale is that the economic outlook is not well described by official forecasts at other meetings, so a shock series that uses cash rate changes announced at those meetings may not adequately account for anticipatory policy. Furthermore, as noted above, the extra power is not necessary.
Approaches 6–9 relax these assumptions by using cash rate changes from all meetings. Whereas our baseline first-stage specification was estimated using only one observation per quarter, these four approaches use monthly data. Approach 6 explains monthly changes in interest rates since 1991 with the most recent official forecast. For example, the August SMP forecasts are used to explain decisions in August, September and October (rather than just the August decision, as in our baseline). The first-stage regression uses data from all Board meetings; we then sum the residuals that fall within a given quarter to derive a quarterly series of policy shocks. This is similar to the baseline approach of Cloyne and Hürtgen (2016).
As discussed in Section 2.1, SMP forecasts are finalised after Board decisions are announced and thus incorporate financial market and other reactions to the announcement. The next few alternatives use forecasts that are finalised before policy decisions are announced, in order to address this concern more explicitly.
Rather than using the Tulip and Wallace (2012) data for official forecasts, for Approach 7 we collect internal staff forecasts from the Bank's unpublished archives. In forecast months, these forecasts, shown in Figure 3, are those tabulated in the Board paper or presented to the Bank's internal Policy Discussion Group in the lead-up to the Board meeting. In other months, they are an archive of the forecasts made prior to the Board meeting. These forecasts are not official and often seem to reflect an incomplete incorporation of new data. They are not usually tabulated in the official Board papers and it is unclear the extent to which the information these forecasts contain is conveyed to the Board (in non-forecast-month meetings). Moreover, the archives are only available from 2001 onwards and have not been consistently maintained. Like Approach 6, we estimate the first-stage regression using interest rate changes from every Board meeting, rather than just the forecast-month meetings.
Rather than using the RBA's forecasts for quarterly underlying inflation and GDP growth, for Approach 8 we use Consensus Economics forecasts for year-ended growth in the headline CPI for the coming and following December quarter along with Consensus forecasts for year-average growth in GDP for the current and following calendar year (see Appendix C). Because Consensus forecasts are compiled around the middle of the month, we assign each set of forecasts to the following month's Board meeting. For example, we assign the survey conducted on 13 April 2015 to the Board meeting on 5 May 2015.[14] The Consensus data allow us to estimate the first-stage regression using data at a monthly frequency. This has similar advantages as Approach 7. One disadvantage is that Consensus forecasts imperfectly capture the central bank's forward-looking behaviour. In practice, however, Tulip and Wallace (2012) showed that Consensus forecasts have very similar properties to RBA forecasts. Cloyne and Hürtgen (2016, Section IV.C) find that their estimates for the United Kingdom using private sector forecasts are almost identical to estimates using Bank of England forecasts.
The specification we use in Approach 9 is the same as Approach 8, but extends the estimation sample for both the first- and second-stage regressions back to 1985:Q3 by incorporating data from the Business Review Weekly's quarterly survey of market economist forecasts. Using earlier data allows us to estimate policy effects with more precision, since policy shocks were much larger prior to the inflation-targeting era. In particular, it captures the high interest rates of the late 1980s, which were followed by a large reduction in inflation.
A third set of alternative specifications depart more fundamentally from the approach of Romer and Romer (2004) in that they do not use economic forecasts. In these specifications, we calculate policy ‘surprises’ using the daily changes in the bank bill interest rate around the policy announcements. Previous studies that have estimated macroeconomic effects of monetary shocks extracted from financial market data include Faust, Swanson and Wright (2004) and Barakchian and Crowe (2013). We consider measures based on both the 1-month (Approach 10) and 3-month (Approach 11) bank bill rates (see Appendix C). Lastly, Approach 12 considers the results if we use a shock series obtained from the recursive VAR in Figure 1.
As can be seen in Figure 7, every shock measure we consider generates a price puzzle. At a horizon of eight quarters, every response is significantly different from zero at the 10 per cent level. This highlights that the price puzzle in Australia is robust to a wide range of specifications designed to control for anticipatory policy.
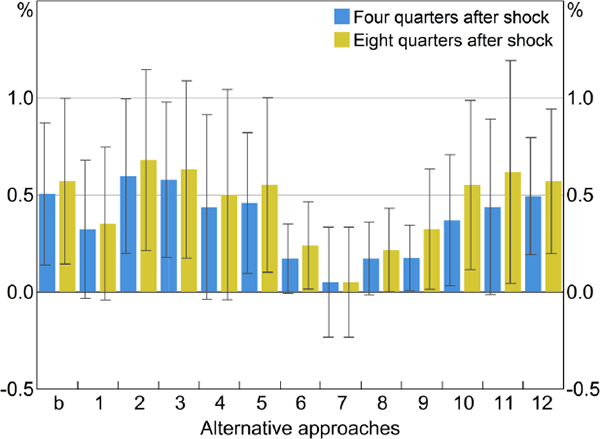
We show the sensitivity analysis for the effect of monetary policy on output in Figure 8. Our baseline estimates (i.e. those shown in Figure 6) are near the middle of the estimates from our 12 alternative specifications, most of which point to an effect that is ‘correctly’ signed but statistically indistinguishable from zero.
Notes: ADL model; blue bars show the cumulated response of real GDP four quarters after a permanent 1 percentage point shock to the cash rate, using the 12 alternative approaches for constructing the cash rate shock; olive bars show the response after eight quarters, and black lines are 90 per cent confidence intervals; sample period for most estimates is 1994:Q2–2015:Q4, exceptions are: Approach 4, which begins in 1996; Approach 7, which begins in 2001; Approach 8, which begins in 1990; and Approach 9, which begins in 1988:Q3
Sources: ABS; Authors' calculations; Business Review Weekly; Consensus Economics; RBA
3.1 VAR Model
Including our new measure of monetary shocks into a VAR permits an easier comparison with other studies. Unlike the six-variable VAR in Figure 1, we use a more parsimonious model that contains only real GDP (in levels), underlying inflation and our measure of monetary policy shocks (in that order). We do not include other variables because we have already isolated a policy shock in the first stage, so including variables such as the exchange rate will unnecessarily strip out useful variation from our measure of policy shocks. This is also closer to the specification used in Romer and Romer (2004). Because VARs are typically based on the cash rate in levels, we cumulate our measure of shocks over time.
Figure 9 presents the impulse response functions (IRFs) of the price level to a temporary 1 percentage point shock to the cash rate. We present IRFs for both our ‘baseline’ shock series and our 12 alternative approaches. The policy experiment considered here involves a less persistent shock to policy than the permanent shock we simulated in the ADL model. Accordingly, while the responses of output and prices are qualitatively similar to the ADL models, they tend to be smaller and more transitory. Across most specifications we consider, a price puzzle is evident.
Notes: VAR model; Cholesky decomposition, with ordering: GDP, underlying inflation, cash rate shocks; blue bars show the cumulated response of inflation four quarters after a temporary 1 percentage point shock to the cash rate, using the 12 alternative approaches for constructing the cash rate shock; olive bars show the response after eight quarters, and black lines are 90 per cent confidence intervals; sample period for most estimates is 1991:Q2–2015:Q4, exceptions are: Approach 4, which begins in 1996; Approach 7, which begins in 2001; Approach 8, which begins in 1990; and Approach 9, which begins in 1988:Q3
Sources: ABS; Authors' calculations; Business Review Weekly; Consensus Economics; RBA
4. What's Going on?
As noted above, we are surprised at the robustness of the price puzzle in Australian data. We are not able to explain this, though several possible arguments are worth noting.
First, one may be tempted to argue that the RBA's forecasts of inflation are uninformative or that the Bank does not respond to these forecasts, and that this explains our findings. However, neither of these claims seems consistent with the evidence. More importantly, they fail to explain the existence of a price puzzle in the first place.
The Romer and Romer (2004) approach would potentially fail if Board members ignore the Bank's official forecasts and instead rely on their own forecasts when setting monetary policy. If the Board's own forecasts were accurate, then policy would be correlated with future inflation in a way we do not control for. However, this possibility seems less likely in Australia than it does in other countries. In other central banks, forecasts and policy are decided by disjoint groups who have separate responsibility for them. In Australia, both forecasts and policy are led by the Governor and Deputy Governor and both are officially the responsibility of the Bank. Moreover, evidence for the United States suggests that FOMC members are unable to improve on staff forecasts (Romer and Romer 2008), which suggests that private information sets of Board members are unlikely to be driving our results.
Another reason why our findings may differ from those of Romer and Romer (2004) is that the latter are sensitive to plausible variations in specification or sample period (Coibion 2012; Barakchian and Crowe 2013). However, this then creates the bigger puzzle of why controlling for anticipatory policy using official forecasts does not reliably work using US data either. If one dismisses the role of anticipatory policy, it is not clear what the alternative explanation for the price puzzle is.
Castelnuovo and Surico (2010) argue that the price puzzle reflects passive monetary policy. They note that increases in inflation in the 1970s were followed by weak monetary policy responses that were insufficient to reverse the inflationary pressure. Hence interest rate increases preceded increases in inflation. This argument may explain why increasing inflation followed interest rate increases. It does not explain why inflation should follow a monetary policy shock, the way it is defined using the Romer and Romer (2004) approach. Persistent or rising inflation, if it is systematic, should be reflected in the central bank forecasts and hence purged from the shock series. It does not seem likely that RBA forecasts systematically failed to detect inflationary pressures on average over the inflation-targeting period. Tulip and Wallace (2012, Section 4.3) report that RBA forecasts of inflation have been more accurate than those of the private sector.
One possibility raised in the literature is the ‘supply’ (or ‘cost’) channel of monetary policy (for an overview, see Castelnuovo (2012)). The idea is that increases in interest rates raise firms' costs (either fixed or marginal, the issues are somewhat different) and hence are passed on in higher prices. We are not aware of evidence that the cost channel is important in Australia, which may reflect that it has not been thoroughly investigated. However, to the extent that it exists, the cost channel might be expected to take longer than the one-quarter lag we estimate in Figures 1 and 2, given that other cost shocks (such as changes in exchange rates or wages) are estimated to flow through to prices with much longer lags.
A more fundamental challenge to the conventional view of monetary policy is the ‘neo-Fisher’ hypothesis of Schmitt-Grohé and Uribe (2014) or Cochrane (2016). They argue that real interest rates are insensitive to monetary policy and hence that an increase in nominal rates will be reflected in a one-for-one increase in inflation. There are several empirical and theoretical objections to the neo-Fisher hypothesis, some of which we note in the introduction. An additional objection is that the neo-Fisher hypothesis would imply a substantial lag from the increase in interest rates to any change in inflation. However, as shown in Figures 1 and 2, the price puzzle emerges the quarter following a change in monetary policy.
5. Large-scale Structural Econometric Models
The price puzzle found in VARs contrasts with the results from large-scale structural econometric models, the approach that VARs were designed to replace. In Figure 10 we show estimates from two large-scale models of the Australian economy: the AUS-M model of Outlook Economics and the Global Economic Model of Oxford Economics. The orange lines trace out the effect on the quarterly inflation rate of a 1 percentage point increase in the cash rate, for one quarter, after which interest rates are endogenous (an experiment that facilitates comparisons with VARs). The blue lines show the effect of a 1 percentage point increase in the cash rate for four quarters, after which it responds endogenously (a more common experiment with these kinds of models).
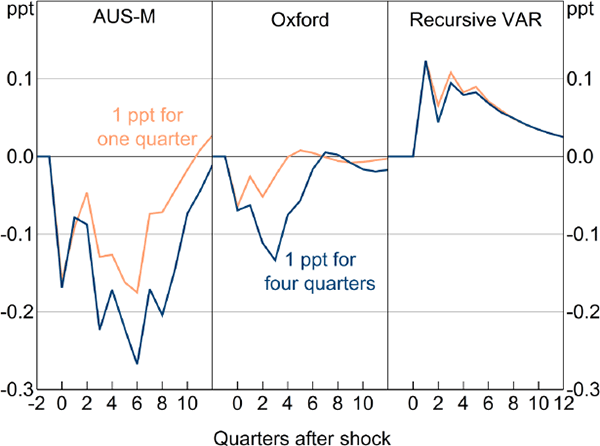
Notes: Inflation is based on the headline consumer price index in the AUS-M and Oxford Economics' Global Economic Model, and the trimmed mean measure for the recursive VAR
Sources: ABS; Authors' calculations; Outlook Economics; Oxford Economics
In contrast to the results presented earlier, the large-scale models estimate that inflation and the price level will fall in response to an interest rate increase (Figure 10). This result is in line with that of large-scale models of the US economy, such as the FRB/US model (Reifschneider, Tetlow and Williams 1999, p 8) and the Fairmodel (Fair 2013, p 180).
A precise decomposition of why the large-scale models give the opposite result to VARs would be complicated. But at the risk of over-generalising, the large-scale models appear to have larger Phillips curve and exchange rate effects than shown in Figure 2. That may reflect the exclusion of wages and the unemployment rate from VARs. It may also reflect the shorter sample period of the VAR. However, a large part of the difference seems to be that interest rates are excluded by assumption from the inflation equation in the large-scale models, but not in VARs. This reflects methodological differences discussed below.
Estrella (2015) highlights the importance of the restrictions on lagged effects of interest rates in reduced-form equations for inflation. Using US data and an otherwise standard structural VAR, Estrella finds that excluding the first lag of the federal funds rate eliminates the price puzzle. He argues this restriction can be motivated by the ‘well-established stylized fact’ that monetary policy operates with long lags. He also presents a simple theoretical model – one without any direct channel from the lagged interest rate to inflation – consistent with this restriction.
The structural VAR developed for Australia by Dungey and Pagan (2000, 2009) also omits interest rates from the inflation equation. It is noteworthy therefore that this model does not exhibit a price puzzle. However, Dungey and Pagan's specification differs from a ‘standard’ structural VAR for reasons other than this restriction; for example, it is a large (11-variable) model that imposes a range of theoretically-motivated restrictions on contemporaneous and lagged effects.
In a more parsimonious VAR such as the one used in Section 1.1, excluding lags of interest rates from the inflation equation is not sufficient to eliminate the price puzzle; although the price puzzle is smaller than the model that does not impose this constraint and is no longer statistically significant. This is true whether we omit the first lag of the cash rate or all three lags from the reduced-form inflation equation.[15] Thus, although the presence of lagged interest rates in the inflation equation is likely to exacerbate the price puzzle, excluding this variable from the model is unlikely to be a panacea.
The above discussion raises important methodological issues. Plausible estimates of the effect of interest rates on inflation seem to come from modelling approaches that involve detailed inspection and respecification of individual equations. This often involves imposition of zero restrictions when estimated coefficients are insignificant or inconsistent with theory or other information. This is standard practice in large-scale models, but can also be done in a VAR (e.g. Dungey and Pagan 2000, 2009). However, these issues are controversial. Equation-by-equation respecification seems to be inconsistent with the rationale for VARs originally proposed by Sims (1980), who argued for common specification across equations.
6. Implications of Our Results
We experimented with three different approaches – a typical VAR with a recursive identification strategy, the Romer and Romer (2004) approach using RBA forecasts, and a measure of monetary ‘surprises’ – all of which generated a perverse response of inflation to monetary policy. This is surprising. The Romer and Romer approach, in particular, seems at least conceptually to be an obvious strategy for removing the price puzzle, if the cause of the price puzzle is anticipatory monetary policy.
Until we can resolve the price puzzle in a robust way, VAR models will not give us credible estimates of the effect of the Bank's policy instrument – the cash rate – on its key policy objective – the rate of inflation. This is a serious problem, given that VARs have been a leading tool for estimating policy and forecast multipliers.
The existence of a price puzzle also casts serious doubts on the response of output to monetary policy in VAR models. We are concerned that the existence of a price puzzle may be symptomatic of fundamental misspecification. If we have failed to identify the effect of a monetary policy shock on inflation, it is hard to see how we can assume that the same monetary policy shock will yield a reliable estimate for output. This concern is rarely discussed in studies that focus on estimating output responses.
Appendix A: Details of the VAR
Data and estimation code for our main results are available at https://www.rba.gov.au/publications/rdp/2017/2017-02-data.html.
The VAR used to create Figures 1 and 2 contains six variables, in order:
US real gross domestic product: The natural logarithm of seasonally adjusted quarterly real US GDP (Datastream code: USGDP…D).
Commodity prices: Index of commodity prices in US dollars (RBA statistical table I2 Commodity Prices).
Real gross domestic product: Seasonally adjusted chain volume GDP (ABS Cat No 5206.0).
Underlying inflation: Quarterly inflation of the trimmed mean consumer price index excluding interest and tax changes (RBA statistical table G1 Consumer Price Inflation).
Overnight cash rate: Overnight cash rate, averaged over the quarter. Nominal official cash rate until June 1998, and then the interbank overnight rate (RBA statistical table F1.1 Interest Rates and Yields – Money Market).
Real trade-weighted index: The real trade-weighted exchange rate index (RBA statistical table F15 Real Exchange Rate Measures).
The VAR is estimated using quarterly data from 1990:Q2 to 2015:Q4, with a lag length of three. It uses a recursive identification scheme: monetary policy is assumed to respond to, but not to affect, other variables contemporaneously, with the exception of the real exchange rate. We follow previous studies by constraining Australian variables from affecting the two foreign variables, either contemporaneously or with a lag. Our estimates are not sensitive to whether we order the cash rate or the real exchange rate last.
Appendix B: Additional Results
Notes: Price level is the cumulated response of underlying inflation; the IRFs are identified using a Cholesky decomposition with ordering: US GDP, commodity prices, GDP, underlying inflation, factor variable 1, factor variable 2, the cash rate, and the real TWI; confidence bands indicate 90 per cent intervals; sample period is 1990:Q2–2015:Q4
Sources: ABS; Authors' calculations
| Coefficient | Standard error | |
|---|---|---|
| Forecasts | ||
Underlying inflation 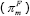 |
−0.05 | 0.05 |
Real GDP growth 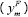 |
0.05 | 0.03 |
| Change in forecasts relative to previous forecast round | ||
Underlying inflation 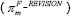 |
0.24*** | 0.08 |
Real GDP growth 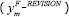 |
0.01 | 0.05 |
Unemployment rate nowcast  |
0.00 | 0.01 |
| Cash rate prior to meeting (rm − 1) | 0.01 | 0.02 |
| Constant (α) | −0.10 | 0.19 |
|
Notes: Adjusted R2 = 0.20, Durbin-Watson = 1.90, No = 100; *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; Newey-West HAC standard errors Sources: ABS; Authors' calculations; RBA |
||
Appendix C: Forecast Data and Alternative Specifications
This appendix provides further details of the forecast data used for our baseline specification and the 12 alternative specifications discussed in Sections 3 and 5.
Baseline specification
Our baseline specification uses RBA forecasts, as documented by Tulip and Wallace (2012). The status, nature and timing of these have changed over time. Since 2007, inflation and output forecasts have been prepared for the SMP, published a few days after the February, May, August and November Board meetings. Between mid 1998 and late 2007, GDP forecasts were those prepared for the Joint Economic Forecasting Group (JEFG) meetings, held in March, June, September and December. Over the same period, inflation forecasts are those for SMP.
We allocate both the inflation and GDP forecasts to the mid-quarter (i.e. forecast-month) meetings, rather than the end-quarter (i.e. JEFG-month) meetings during 1998–2007. We do this because the cash rate was more likely to be adjusted during forecast-month meetings and because our interest is primarily in estimating the effects of monetary policy on inflation, rather than GDP. However, this decision does create a problem in that the GDP forecasts in particular may embody the effects of the policy decision taken in the mid-quarter meeting and any new data. However, our baseline results are not qualitatively affected if we re-estimate our models using cash rate changes in end-quarter Board meetings over this period.
Prior to 1998, both the inflation forecasts and GDP forecasts in the Tulip and Wallace dataset were those prepared for the JEFG meetings, and thus our measure of interest rates changes refers to the end-quarter Board meetings for this period.
Approach 8
Consensus Economics has conducted a monthly survey of two dozen private sector forecasters since 1990. The survey provides calendar-year average forecasts for real GDP growth and year-ended forecasts (to December quarter) for CPI inflation. The advantage of Consensus forecasts relative to official RBA forecasts is that the former are actively updated every month, while the RBA only undertakes a formal forecasting round once per quarter.
For this approach, the first-stage regression includes the current and following years' Consensus forecasts for GDP growth and headline inflation, and the revisions to these forecasts relative to the previous month's survey. We also include dummies for the calendar month of the Board meeting, to control for the fact that the horizon of the forecasts will depend on the calendar month. For example, the forecast for the current calendar year made in January will relate to the next 12 months, while the forecast made in December will largely incorporate data already received. For Board meetings held in February, it is not possible to define a revision to the following year's forecast; for these observations, we set the missing forecast data to zero. The dummy for the calendar month of February will absorb the fact that we set the revisions to zero. We omit the unemployment rate.
Approach 9
Since Consensus and official RBA forecasts are not available prior to 1990, we use Business Review Weekly's (BRW) survey of market economist forecasts to include the period from 1985 to 1990. BRW's survey was conducted once per quarter, typically during the final month of the quarter, and provided financial-year average forecasts for GDP growth and year-ended forecasts for headline CPI (to June quarter).
While BRW provided forecasts for both the current year and following years, the time-series data is only complete for the current-year forecasts. In cases where forecasts for the following year are missing, we set these observations equal to zero and include a dummy that equals one if the data are missing, and zero otherwise. From 1991 onwards, we use the Consensus survey of market economist forecasts.
We assign each forecast, whether Consensus or BRW, to the closest Board meeting, ensuring that the forecasts were always generated prior to the meeting. To do this, we use the precise date on which the survey was administered and the date of the Board meeting in question. After 1990, which is the period in which we have monthly forecasts from Consensus, the forecasts were generated on average 23 days prior to each meeting. The time lag between the publication of the forecasts and the relevant Board meeting was longer prior to 1990 – averaging 53 days – and more variable, due to the quarterly frequency of the BRW survey. This long time lag means that we cannot control for anticipatory policy as effectively prior to 1990. We include a control for this time lag (in days) in the first-stage regression. As with Approach 8, we also include a full set of month dummies in the first stage.
The first-stage regression uses data on every Board meeting since October 1985, giving 330 observations. Since the Bank only began announcing cash rate outcomes from 1990 onwards, for the period before January 1990 we approximate the change in the target cash rate using the change in the actual cash rate. Specifically, we use the change in the interbank rate that prevailed immediately before the current meeting to the interbank rate that prevailed immediately prior to the subsequent meeting, using three-day averages to smooth out volatility in the data. We extract the residuals from this regression as our measure of policy shocks and aggregate the shocks to quarterly frequency by summing across all meetings in the quarter.
Approaches 10 and 11
In addition to the forecast-based procedure in Romer and Romer (2004), we can also identify policy shocks using measures of the surprise component of monetary policy decisions.
We follow Kearns and Manners (2005) in using daily changes in yields on 1- or 3-month bank bills to measure the policy surprise. Since our data on output and inflation are at quarterly frequency, we construct a quarterly measure of policy surprises summing across all surprises in the quarter. We do not use futures contracts over the cash rate to estimate policy surprises because intraday data on ASX 30-day interbank cash rate futures are only available from 2003 onwards.
References
Barakchian SM and C Crowe (2013), ‘Monetary Policy Matters: Evidence from New Shocks Data’, Journal of Monetary Economics, 60(8), pp 950–966.
Beechey M and P Österholm (2008), ‘A Bayesian Vector Autoregressive Model with Informative Steady-State Priors for the Australian Economy’, Economic Record, 84(267), pp 449–465.
Berkelmans L (2005), ‘Credit and Monetary Policy: An Australian SVAR’, RBA Research Discussion Paper No 2005-06.
Bernanke BS, J Boivin and P Eliasz (2005), ‘Measuring the Effects of Monetary Policy: A Factor-Augmented Vector Autoregressive (FAVAR) Approach’, The Quarterly Journal of Economics, 120(1), pp 387–422.
Brischetto A and G Voss (1999), ‘A Structural Vector Autoregression Model of Monetary Policy in Australia’, RBA Research Discussion Paper No 1999-11.
Castelnuovo E (2012), ‘Testing the Structural Interpretation of the Price Puzzle with a Cost-Channel Model’, Oxford Bulletin Of Economics And Statistics, 74(3), pp 425–452.
Castelnuovo E and P Surico (2010), ‘Monetary Policy, Inflation Expectations and the Price Puzzle’, The Economic Journal, 120(549), pp 1262–1283.
Cloyne J and P Hürtgen (2016), ‘The Macroeconomic Effects of Monetary Policy: A New Measure for the United Kingdom’, American Economic Journal: Macroeconomics, 8(4), pp 75–102.
Cochrane JH (2004), ‘Comments on “A New Measure of Monetary Shocks: Derivation and Implications”’, Presentation to the Economic Fluctuations and Growth Research Meeting, National Bureau of Economic Research Summer Institute, Cambridge, 17 July. Available at <http://faculty.chicagobooth.edu/john.cochrane/research/papers/talk_notes_new_measure_2.pdf>
Cochrane JH (2016), ‘Do Higher Interest Rates Raise or Lower Inflation?’, Unpublished manuscript, The University of Chicago Booth School of Business, February. Available at <http://faculty.chicagobooth.edu/john.cochrane/research/papers/fisher.pdf>.
Coibion O (2012), ‘Are the Effects of Monetary Policy Shocks Big or Small?’, American Economic Journal: Macroeconomics, 4(2), pp 1–32.
Dungey M and A Pagan (2000), ‘A Structural VAR Model of the Australian Economy’, Economic Record, 76(235), pp 321–342.
Dungey M and A Pagan (2009), ‘Extending a SVAR Model of the Australian Economy’, Economic Record, 85(268), pp 1–20.
Estrella A (2015), ‘The Price Puzzle and VAR Identification’, Macroeconomic Dynamics, 19(8), pp 1880–1887.
Fair RC (2013), Macroeconometric Modeling, Economics 116a class reference material, Yale University, Department of Economics, November. Available at <https://fairmodel.econ.yale.edu/mmm2/mm.pdf>.
Faust J, ET Swanson and JH Wright (2004), ‘Identifying VARS Based on High Frequency Futures Data’, Journal of Monetary Economics, 51(6), pp 1107–1131.
Galí J (2008), Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework, Princeton University Press, Princeton.
Gerard H and K Nimark (2008), ‘Combining Multivariate Density Forecasts Using Predictive Criteria’, RBA Research Discussion Paper No 2008-02.
Heath A (2015), ‘The Role of the RBA's Business Liaison Program’, Address to the Urban Development Institute of Australia (Western Australia Division Incorporated) Luncheon, Perth, 24 September.
Jääskelä J and D Jennings (2010), ‘Monetary Policy and the Exchange Rate: Evaluation of VAR Models’, RBA Research Discussion Paper No 2010-07.
Jacobs D and V Rayner (2012), ‘The Role of Credit Supply in the Australian Economy’, RBA Research Discussion Paper No 2012-02.
Kearns J and P Manners (2005), ‘The Impact of Monetary Policy on the Exchange Rate: A Study Using Intraday Data’, International Journal of Central Banking, 2(4), pp 157–183.
Lawson J and D Rees (2008), ‘A Sectoral Model of the Australian Economy’, RBA Research Discussion Paper No 2008-01.
Mankiw NG (2015), Macroeconomics, 9th edn, Worth Publishers, New York.
Phan T (2014), ‘Output Composition of the Monetary Policy Transmission Mechanism: Is Australia Different?’, Economic Record, 90(290), pp 382–399.
RBA (Reserve Bank of Australia) (2015), ‘Domestic Market Operations’, viewed December 2016.
Reifschneider D, R Tetlow and J Williams (1999), ‘Aggregate Disturbances, Monetary Policy, and the Macroeconomy: The FRB/US Perspective’, Federal Reserve Bulletin, 85(1), pp 1–19.
Romer CD and DH Romer (2000), ‘Federal Reserve Information and the Behavior of Interest Rates’, The American Economic Review, 90(3), pp 429–457.
Romer CD and DH Romer (2004), ‘A New Measure of Monetary Shocks: Derivation and Implications’, The American Economic Review, 94(4), pp 1055–1084.
Romer CD and DH Romer (2008), ‘The FOMC Versus the Staff: Where Can Monetary Policymakers Add Value?’, The American Economic Review, 98(2), pp 230–235.
Rusnak M, T Havranek and R Horvath (2013), ‘How to Solve the Price Puzzle? A Meta-Analysis’, Journal of Money, Credit and Banking, 45(1), pp 37–70.
Schmitt-Grohé S and M Uribe (2014), ‘Liquidity Traps: An Interest-Rate-Based Exit Strategy’, The Manchester School, 82(Supplement S1), pp 1–14.
Sims CA (1980), ‘Macroeconomics and Reality’, Econometrica, 48(1), pp 1–48.
Sims CA (1992), ‘Interpreting the Macroeconomic Time Series Facts: The Effects of Monetary Policy’, European Economic Review, 36(5), pp 975–1000.
Stevens G (1999), ‘Six Years of Inflation Targeting’, Address to the Economic Society of Australia, Sydney, 20 April.
Suzuki T (2004), ‘Is the Lending Channel of Monetary Policy Dominant in Australia?’, Economic Record, 80(249), pp 145–156.
Tulip P and S Wallace (2012), ‘Estimates of Uncertainty around the RBA's Forecasts’, RBA Research Discussion Paper No 2012-07.
Woodford M (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press, Princeton.
Acknowledgements
We would like to thank Anthony Brassil, Efrem Castelnuovo, Christian Gillitzer, Jarkko Jääskelä, Dan Rees and John Simon for useful comments and suggestions. The views expressed in this paper are our own and do not necessarily reflect those of the Reserve Bank of Australia. We are solely responsible for any errors.
Footnotes
Other variables in the VAR, namely US GDP and commodity prices, are assumed to be unaffected by Australian interest rates. These and other specification details are discussed in Appendix A. [1]
The recursive inflation equation includes contemporaneous observations of US real GDP, commodity prices and real GDP but only lagged observations on the cash rate and the real exchange rate. To examine the stability of the price puzzle, we estimated the recursive inflation equation over an eight-year rolling window. These rolling regressions revealed that the ‘wrong’ sign on the first lag of the cash rate is primarily a feature of the second half of our sample period (i.e. from the late 1990s onwards). In the early 1990s, the coefficient on the first lag of the cash rate is close to zero. [2]
In other papers, Romer and Romer (2000, 2008) found the Federal Reserve's forecasts of inflation were a sufficient statistic for the inflation outlook, that is, other data (such as the forecasts of the private sector or the Federal Open Market Committee (FOMC)) do not provide useful additional information. [3]
The central bank also reacts to predicted inflation in the current quarter, but for simplicity we subsume this into the forecast. [4]
In addition to purging the policy rate of systematic responses to forecasts, Romer and Romer (2004) also use a historical narrative approach to remove movements in the actual federal funds rate (FFR) due to reasons unrelated to the stance of monetary policy. Such movements in the FFR are endogenous to economic conditions, and so using the actual FFR could lead to biased estimates of the effect of monetary policy on output and inflation. We do not need to create a series of intended policy changes, because over the sample period we consider (1990–2015), the target cash rate is the intended target policy rate. The RBA's domestic market operations have also ensured that the actual cash rate has remained close to the target rate (see Graph 1 in RBA (2015)). [6]
The Tulip and Wallace dataset does not contain inflation or GDP forecasts for 1991:Q3 or 1993:Q3. For these quarters, we interpolate forecasts using official forecasts from neighbouring quarters and Consensus forecasts for year-average growth in headline CPI and GDP. [7]
We also decide to include forecasts in year-ended percentage changes because that is how the forecasts are tabulated in the SMP and Board papers, and how they are presented to the RBA Board. Our archival forecast data do not contain quarter-on-quarter inflation forecasts prior to 2001. [8]
Where available, we use forecast data archived immediately before (or for the purpose of) the relevant Board meeting. If these forecasts are not available, we use the forecasts presented to the internal Policy Discussion Group, which is held on the Wednesday prior to the Board meeting, or to the Economic Group policy meeting. [9]
The few instances where the blue dots lie above the 45 degree line follow very large reductions in the cash rate, notably the 100 basis point cut in February 2009 and the 50 basis point cut in May 2012. [10]
When we omit the inflation forecasts from the model, the forecasts for output growth are jointly significant. In addition to multicollinearity, the insignificance of the GDP forecasts may be because the forecasts are not expressed in ‘gap’ terms; we find that replacing the GDP forecasts with forecasts for the unemployment rate leads to significant coefficient estimates (see Section 3). [11]
Romer and Romer (2004) estimate their ADL models using monthly data on industrial production and inflation. They use three years of lags for the policy shock in the output specification and four years in the inflation specification. We include three years of lags in both specifications, but our results are not affected by this decision. [12]
We also include revisions to the forecasts out to four quarters ahead. [13]
Assigning each Consensus forecast to the following month's Board meeting ensures that the forecasts do not capture information that would not have been available to the Board in real time (or the effect of the policy decision itself on the forecast). [14]
At first glance, the results in Figure 2 seem to imply that if we omit lagged interest rates from the inflation equation that the price puzzle will completely disappear. However, in Figure 2 this restriction was imposed after estimation, holding other coefficients constant. The other coefficients in the inflation equation will change if interest rates are excluded, picking up some of their correlation. [15]