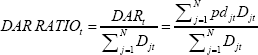RDP 2016-09: Why Do Companies Fail? 6. Robustness Tests and Extensions
November 2016
6.1 Alternative Models
The estimates from the benchmark model are robust to changes in the sample period, the treatment of outliers and the inclusion of company-specific random effects.[21] In addition, we have estimated the benchmark specification using a range of models that are more standard in the literature:
- a continuous-time survival model – the semi parametric CPH model;
- a discrete-time survival model with a logit, rather than complementary log-log link function; and
- logit and probit binary dependent variable models.
The key results from these models are similar to those from the benchmark model and are available on request.
6.2 Listed Versus Unlisted Companies
Next, we briefly consider whether the determinants of failure differ for listed and unlisted companies in Australia. We estimate the benchmark model for listed and unlisted companies separately. The results are shown in Table 3.
The effects of the cyclical variables on the predicted probability of failure vary somewhat when estimated separately on the listed and unlisted company sub-samples. For instance, size is more closely associated with failure among listed companies, while age seems to be more closely associated with failure for unlisted companies. More notably, the type of leverage seems to matter. Debt appears to be associated with failure only for listed companies, while trade credit matters for both types of company.
The results also suggest that, for unlisted companies, subsidiaries are significantly less likely to fail, particularly subsidiaries of foreign parents. This suggests that the liquidity and solvency of subsidiary companies are closely tied to the performance of their parent companies. To the extent that business performance is not perfectly correlated across subsidiaries within the parent company, these results are consistent with internal capital markets effectively insulating subsidiaries from liquidity shocks through cross-subsidisation (Becchetti and Sierra 2003; Dewaelheyns and Van Hulle 2006).[22]
| Listed companies | Unlisted companies | |
|---|---|---|
| Structural characteristics | ||
| Public | 0.23* (0.08) |
|
| Domestic subsidiary (not foreign subsidiary) |
na | −0.19** (0.01) |
| Foreign subsidiary (not domestic subsidiary) |
na | −0.61*** (0.00) |
| Cyclical characteristics | ||
| Log of age | −0.00 (0.98) |
−0.17*** (0.00) |
| Log of assets | −0.17** (0.03) |
−0.00 (0.93) |
| Debt-to-assets ratio | 0.41*** (0.00) |
0.03 (0.25) |
| Trade credit-to-assets ratio | 0.33* (0.08) |
0.11*** (0.00) |
| Cash-to-assets ratio | −0.18*** (0.01) |
−0.19*** (0.00) |
| Return on assets | −0.50*** (0.00) |
−0.11*** (0.00) |
| Time fixed effects | Yes | Yes |
| Industry fixed effects | Yes | Yes |
| Observations | 18,150 | 72,578 |
| Companies | 1,755 | 21,661 |
| Failure observations | 137 | 395 |
|
Notes: Average marginal effects are calculated for each company based on the observed values of the explanatory variables for that company and averaged across companies; standard errors are calculated using the delta method; p-values are reported in parentheses; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent level, respectively; for structural characteristics, marginal effects shown are for a change from base category; for cyclical characteristics, marginal effect of one standard deviation change |
||
6.3 Debt at Risk
We now take the benchmark model estimates and develop a simple framework to measure the potential effect of corporate failure on financial stability. In particular, we construct estimates of debt at risk (DAR) for each company in the sample and then aggregate these estimates to make inferences for the Australian economy. The DAR for each company is constructed as the estimated probability of failure multiplied by the reported stock of debt outstanding on the company's balance sheet. We aggregate the DAR estimates for each individual company at a given point in time and normalise this by the total stock of debt. The result is the share of aggregate debt that is expected to default each year. We refer to this as the DAR ratio or ‘debt-weighted probability of failure’:
where pdjt is the probability of failure estimated from the benchmark model and Djt is the total stock of debt for company j in year t. We also create an alternative measure that, instead of reported (bank and non-bank) debt, uses each company's net trade credit (we call this ‘trade credit at risk’ (TCAR)). The share of TCAR in total trade credit is referred to as the TCAR ratio (or ‘trade credit-weighted probability of failure’). We censor net trade credit at a lower bound of zero in calculating this measure, so that companies that are net trade creditors do not cancel out those that are net trade debtors.
DAR and TCAR are the amounts that creditors could expect to lose if a company fails and there is a 100 per cent loss rate. In a sense, these estimates are an upper bound on creditor losses. But the framework ignores the possibility that a corporate default can have knock-on effects to other companies.[23] The estimates might therefore also underestimate the share of aggregate corporate debt that is at risk of default to the extent that such flow-on effects are important.
By our estimates, around 0.5 per cent of total debt was ‘at risk’ over the sample period, with the share of debt at risk being higher for listed companies than for other companies (Table 4). On top of this, around 0.4 per cent of trade credit was at risk in aggregate. The slightly lower estimate of aggregate risk for trade credit is due to private companies being the main users of trade credit (three-quarters of aggregate trade credit is held by private companies) and private companies are generally at lower risk of failing than public companies.
| Company type | Share of DAR ratio | Share of TCAR ratio | For each company type | |
|---|---|---|---|---|
| Debt as a share of aggregate company debt | Trade credit as a share of aggregate company trade credit | |||
| Public listed | 0.65 | 0.68 | 46.3 | 11.4 |
| Public unlisted | 0.42 | 0.48 | 15.3 | 14.1 |
| Private | 0.43 | 0.38 | 38.4 | 74.5 |
| All companies | 0.53 | 0.43 | 100.0 | 100.0 |
Large companies account for a disproportionate share of debt at risk. Across all companies, more than 90 per cent of aggregate DAR is held by companies in the highest debt quintile. This is in part because our sample is skewed towards larger companies (it covers almost all listed companies, but only a small proportion of unlisted companies), but is also indicative of a large right tail in the distribution of debt at risk.
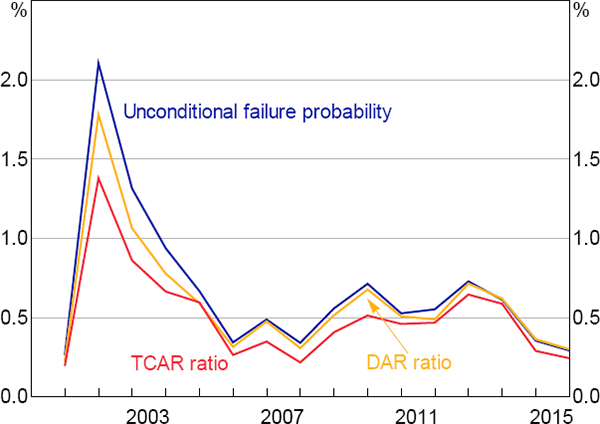
The shares of both debt and trade credit at risk have declined over recent years (Figure 8). This reflects the decline in the estimated failure probabilities, as can be seen by the close correlation with the annual estimate of the unconditional failure probability from the benchmark model. This implies that the drivers of the average failure probability – in particular, macroeconomic conditions – are also a key driver of aggregate corporate credit risk in Australia. The fact that the TCAR ratio is only slightly less cyclical than the DAR ratio suggests trade credit may play a role in propagating aggregate shocks.
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
Footnotes
The company-specific random effect captures the fact that some companies are more prone to failure because of unobserved characteristics, such as management quality, corporate governance structure and risk appetite. In survival analysis terms, some companies are more ‘frail’ than others. The random effects model assumes that the unobserved characteristics are not correlated with any of the observed characteristics that act as control variables. It is plausible that risk appetite is correlated with factors such as leverage, which would violate this assumption. As such, the benchmark model was preferred over the random effects model. [21]
The internal capital markets hypothesis assumes that companies are ‘randomly assigned’ to being subsidiaries or standalone companies. It could be the case that ‘healthy’ companies are more likely to be subsidiaries than unhealthy companies, particularly if they have been identified as a target for acquisition. Alternatively, ‘healthy’ parents with strong management skills and experience may be more likely to establish subsidiaries and the subsidiaries ‘inherit’ this unobserved human capital. These alternative hypotheses suggest that the link between probability of failure and subsidiary status is due to some latent characteristic of the subsidiary (or parent) rather than internal capital market funding. [22]
The spillover effects are captured to some extent by the time fixed effects in the benchmark model in that the year dummies capture the average level of spillovers each year. [23]