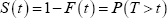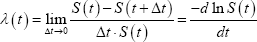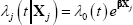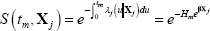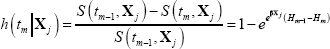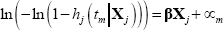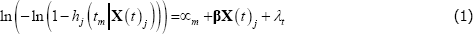RDP 2016-09: Why Do Companies Fail? 3. Modelling Approach
November 2016
Survival analysis is our preferred approach to examine the determinants of corporate failure. We opt for survival models because of the advantages they offer over discrete choice models (e.g. probit or logit models) that are more common in the literature.
The primary advantage of survival analysis is that it parsimoniously accounts for ‘time dependence’; the idea that the probability of failure is a function of company age (which we measure as the time since a company registered). If company age has a significant effect on failure risk, survival analysis is more appropriate than discrete choice models, which often treat failure as a ‘static’ classification problem and do not allow failure risk to evolve over a company's life cycle.
A further advantage of survival analysis is that it explicitly accounts for our limited ability to observe company failure. Many of the companies in the sample do not fail by the end of the sample period and it is not known if (or when) they subsequently fail – the data are ‘right censored’. Listed companies are not observed prior to their listing and unlisted companies are not observed before they apply for a credit report – the data are also ‘left truncated’. Survival analysis controls for both of these problems.
Given that survival models are used infrequently in the corporate failure literature, the next section outlines some basics of survival analysis. The subsequent section explains our preferred approach: a discrete-time survival model. This discussion borrows heavily from Rodríguez (2010) and Gupta, Gregoriou and Healy (2015).
3.1 Basic Outline of Survival Models
Survival analysis involves estimating two key functions – the survival and hazard functions. Standard survival analysis treats time as a continuous variable, and this section proceeds on that basis.
The survival function is the probability of surviving until at least time t: in our case the probability of a company not failing between its registration and time t (inclusive). More formally, let T be a non-negative random variable denoting the time between a company registering and failing. The survival function is:
where F(t) is the cumulative distribution function of T evaluated at t. The survivor function is equal to one when t is equal to zero and approaches zero as t approaches infinity. In the context of corporate failures, this means that a company is certain to fail over a long enough time horizon.
The continuous-time hazard function, λ(t), can be derived based on the survivor function:
This expression states that the hazard function is the (limiting) probability that failure occurs within a given time interval, Δt, given that the company survived to the start of that interval. The continuous-time hazard is not strictly a probability – it has units of probability over time – and is perhaps most easily thought of as an instantaneous failure rate. A hazard rate of zero indicates no risk of failure at that instant while a rate of infinity indicates certain failure at that moment. The hazard rate can vary over time in a non-monotonic way.
A common way to specify the hazard rate is the semi-parametric Cox proportional hazards (CPH) model (Cox 1972). This model assumes the instantaneous risk of failure is a function of ‘time at risk’ (company age in our case) and other risk factors (e.g. company ownership type). In this model, the hazard function for company j at time t is assumed to be:
where Xj is a vector of explanatory variables for company j, β is a vector of coefficients, and the baseline hazard rate, λ0(t), is an unspecified function of time. The baseline hazard rate is the explicitly time-dependent part of the hazard function and corresponds to the hazard rate when all covariate values are equal to zero. The proportionality of the model stems from the multiplicative effect on the baseline hazard of (time-invariant) explanatory variables – if a particular change in an explanatory variable doubles the baseline hazard at t = 1, it does the same at t = 2 and so on. This proportionality simplifies estimation of the continuous-time model.
3.2 Discrete-time Survival Model
Company failure is experienced at an instant in continuous time, which suggests that we should use a continuous-time survival model. This would be appropriate if survival times were recorded in relatively fine timescales (e.g. seconds, hours or days) and there were no tied survival time periods (i.e. no two companies survive for exactly the same length of time).
But these conditions are violated when accounting data are used to model corporate failure. This is because financial reporting typically occurs on coarse timescales. For instance, we observe the state of unlisted companies only every year and listed companies only every six months. In this case, discrete-time models are more appropriate. In effect, we have a case of ‘interval censoring’. This occurs when the event is experienced in continuous time but we only record the time interval within which the event takes place. Interval censoring leads to discrete-time data.
Discrete-time survival models explicitly account for this type of censoring. The discrete-time survival function, based on the continuous-time proportional hazard function above and representing survival to the end of the interval [tm − 1,tm], is:
where 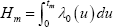 is known as the ‘integrated baseline hazard’.
The discrete-time hazard for the same interval,
h(tm|Xj), follows from the
laws of conditional probability:
is known as the ‘integrated baseline hazard’.
The discrete-time hazard for the same interval,
h(tm|Xj), follows from the
laws of conditional probability:
Applying a complementary log-log transformation:
where ∝m = ln(Hm − Hm − 1) is the log of the baseline hazard evaluated over the interval. A key step in estimating this model is to choose a baseline hazard function. We choose a parsimonious specification for our benchmark model, with the baseline hazard assumed to be a function of the natural log of company age. In unreported results, we estimate a flexible specification that includes separate dummy variables for each company age observed in the sample. This model provides results very similar to the benchmark model.
Some of the explanatory variables used in the analysis vary over time: it is straightforward to extend the above to X(t)j instead of Xj. The explanatory variables include ‘cyclical’ company characteristics, such as size, profitability and leverage. We discuss these explanatory variables in more detail later.
Macroeconomic conditions, such as the state of the business cycle, may also matter. Given the relatively coarse time dimension of our (annual) data, we choose to model the effect of all aggregate conditions jointly, by including time fixed effects, represented by a series of year dummies, λt.[11] The benchmark model is therefore written:
These time fixed effects capture the effects of macroeconomic conditions that are not captured by the variation over time in the firm-level variables. For example, variation in company-level profitability may capture some of the variation in demand growth over the sample period. This set-up works against us finding a significant independent effect of macroeconomic conditions on corporate failure. Notably, the time fixed effects also capture the effect of other aggregate conditions, such as institutional factors (e.g. changes in insolvency legislation) and the average levels of any omitted company-level variables (e.g. risk appetite).
Finally, we cluster the standard errors by company to control for unobserved shocks within a company that may be correlated over time and affect the probability of failure.
Footnote
Models were also estimated in which macroeconomic variables were directly included. These included: 1) real GDP growth for each Australian state (to capture the state-level business cycle); 2) the difference between the interest rate on loans to large businesses and the cash rate (to proxy for aggregate credit risk); and 3) the cash rate (to capture financing conditions). There was some tentative evidence that the credit risk variable was positively correlated with the probability of failure at the company level, but, in general, the results were not very robust. [11]