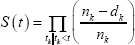RDP 2016-09: Why Do Companies Fail? 5. Results
November 2016
Before estimation it is useful to show how the failure rates of different companies evolve as they grow older. This is neatly summarised by Kaplan-Meier failure estimates. This method estimates the survival probability non parametrically, assuming no specific underlying function. The basic Kaplan-Meier estimate of the probability of surviving beyond time t is:
where tk are points in time indexed by positive integers k, nk is the number of companies eligible for failure at time tk (taking into account right censoring) and dk is the number of companies that fail between time tk − 1 and tk. The failure rate is then simply estimated as 1 minus the survival rate.
Figure 3 shows Kaplan-Meier estimates of the failure rates for publicly listed, publicly unlisted and private companies. These failure curves indicate that, controlling only for age, failure risk varies across ownership types. Across most ages, private companies are significantly less likely to fail than public companies. Within older public companies, listed companies appear to be more risky than unlisted companies. Given the age-dependent nature of this relationship, we allow the effect of ownership type to vary with age in the benchmark model.
Note: Shaded areas represent 95 per cent confidence intervals
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
The estimation results of the benchmark model are shown in Table 2. Note that the reported estimates are average marginal effects. The average marginal effect of a given covariate is the average over the sample of the marginal effect computed for each company observation at the observed values of its covariates (marginal effects in the complementary log-log model are a function of the covariates). The average marginal effects can be interpreted as the change in the probability of failure due to a change in the given covariate, provided other covariates are held constant.
| Structural characteristics | |
|---|---|
| Public (average over the sub-sample of unlisted companies) |
0.43*** (0.01) |
| Listed (average over the sub-sample of public companies) |
0.10 (0.48) |
| Cyclical characteristics | |
| Log of age | −0.12*** (0.00) |
| Log of assets | −0.12*** (0.00) |
| Debt-to-assets ratio | 0.12*** (0.00) |
| Trade credit-to-assets ratio | 0.11*** (0.00) |
| Cash-to-assets ratio | −0.19*** (0.00) |
| Return on assets | −0.13*** (0.00) |
| Time fixed effects | Yes |
| Industry fixed effects | Yes |
| Wald test (p-value) | 0.00 |
| Area under ROC curve | 0.73 |
| Observations | 90,729 |
| Companies | 23,326 |
| Failure observations | 532 |
|
Notes: Standard errors are calculated using the delta method; p-values are reported in parentheses; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent level, respectively; for structural characteristics, marginal effects shown are for a change from private to public company and a change from unlisted to listed company; for cyclical characteristics, marginal effect of one standard deviation change; ROC curve denotes a receiver operator characteristic curve |
|
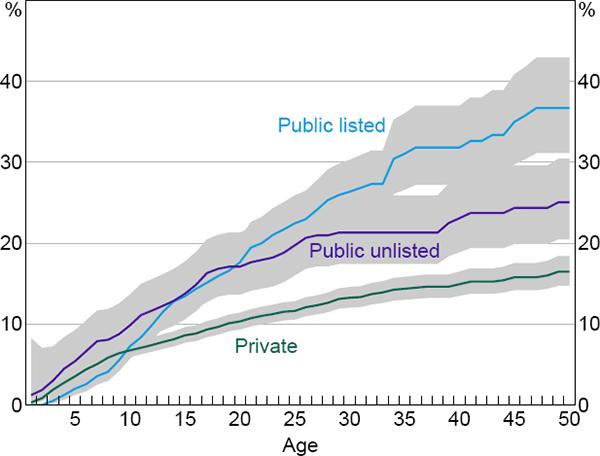
The results indicate that the type of ownership is important in predicting company failure. A public company is around 0.4 percentage points more likely to fail in a given year than a comparable private company. Moreover, listed companies have failure probabilities that differ from unlisted public companies, but in a way that varies over time, so is not visible in the age-invariant average marginal effect above (the full regression results in Appendix A make this clear). Figure 4 shows estimated failure functions for three companies that differ only by their structural characteristics. Private companies are less likely to fail than public companies at almost all ages. Early in their life, publicly listed companies are less likely to fail than comparable unlisted public companies, but this situation reverses and listed companies are less likely to survive beyond 30 years of age. These life-cycle patterns are consistent with the Kaplan-Meier failure curves shown in Figure 3. This indicates that the age profile of failure risk for different types of corporate ownership is not affected by controlling for cyclical and macroeconomic variables.
Note: Estimates from the benchmark model for a company with median cyclical characteristics, in the manufacturing industry, in 2011
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
The higher failure curve for public companies – the gap between the green and purple lines in Figure 4 – is consistent with the hypothesis that public companies take greater risks than private companies because of their greater separation of ownership and control or because of their more dispersed ownership structures (i.e. shareholders of public companies have less ‘skin in the game’). The higher degree of transparency of public companies may also discourage company directors from attempting to restructure the company and instead push them towards insolvency during periods of stress.[18] The higher failure curve for listed companies versus publicly unlisted companies at higher ages – the gap between the blue and purple lines – is also consistent with these ‘agency’ and ‘transparency’ hypotheses.
It is not clear what is driving the result that young publicly listed companies are less likely to fail than young publicly unlisted companies (the area in which the purple line is above the blue line in Figure 4). It might be that companies with better growth prospects self-select into listing at a young age. These ‘superstar’ companies may thus have lower failure probabilities at an early stage of life but this effect dissipates over time. In addition, there may be greater market scrutiny of young listed companies, such that it is more difficult at that stage to take risks.
Not surprisingly, cyclical company-level characteristics are associated with the probability of failure. The signs of the marginal effects of these variables align with our hypotheses. Larger companies are less likely to fail than smaller companies, and older companies are less likely to fail than younger companies. A higher level of debt or trade credit relative to assets raises the probability of failure. The liquidity of a company's balance sheet also matters; more cash lowers the probability of failure, as does higher profitability.
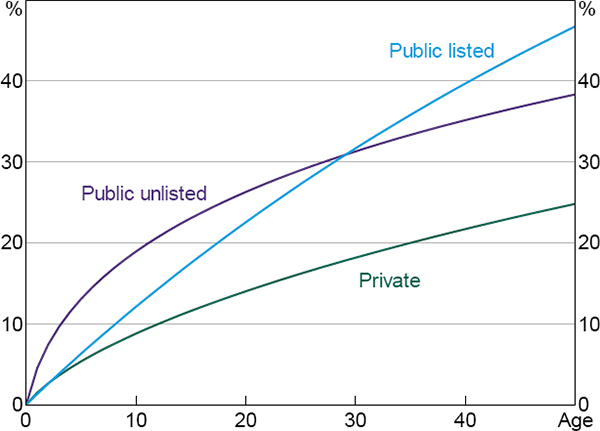
A one standard deviation change in each of the cyclical variables is estimated to change failure probabilities by between 11 and 19 basis points. These effects appear small, but are large in the context of our unconditional failure probability of around 60 basis points. In addition, such differences in cyclical firm-level characteristics can have a ‘cumulative effect’ and lead to significant differences in the probability of failure when measured over a longer time horizon. For example, a one standard deviation increase in the log of total assets – equivalent to a company growing from $12 million in assets to $138 million – is associated with a lower failure probability of about 12 basis points in a given year. But the same increase in size would make an otherwise median private company about 1.7 percentage points less likely to fail over the first 10 years of its life (Figure 5).
Notes: Estimates from benchmark model for a private company with otherwise median cyclical characteristics, in the manufacturing industry, in 2011; changes in the baseline will affect the estimated level of the cumulative impact but will not affect the relative contribution of each of the cyclical company-level factors
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
Leverage from reported debt (bank and non-bank debt) and leverage from trade credit (business-to-business lending) have roughly equal impacts on the probability of failure. A one standard deviation increase in these measures (which is equivalent to around 25 percentage points for both measures) is associated with an increase in failure probability of around 11 basis points over a year, and 1.7 percentage points over a 10-year period.
The effect of liquidity is particularly important; a one standard deviation rise in the cash-to-assets ratio lowers the probability of failure by around 19 basis points over one year, or 2.8 percentage points over the first ten years of life for the median private company. A one standard deviation increase in profitability has a smaller effect, roughly equivalent to that of company size.
The probability of failure varies a lot by industry. This is shown by the marginal effects of the industry dummies (Figure 6). The estimated average marginal effects indicate that, across all companies, construction companies are most prone to fail when controlling for other observable differences between industries. The relatively high failure rate for construction companies led to a Senate inquiry into the industry in 2015. The inquiry listed a wide range of potential causes for the high failure rate in the construction industry, including a heavy reliance on subcontracting, ‘illegal phoenix activity’ and even the weather (Senate Economics References Committee 2015).[19]
The relative ranking of industries in terms of ‘failure risk’ is barely affected by the inclusion of control variables (this is shown by the relative ranking of industries based on both the unconditional failure rate and the average marginal effects in Figure 6). This suggests that variation across industries in company characteristics, such as leverage and profitability, do not fully capture industry risk.
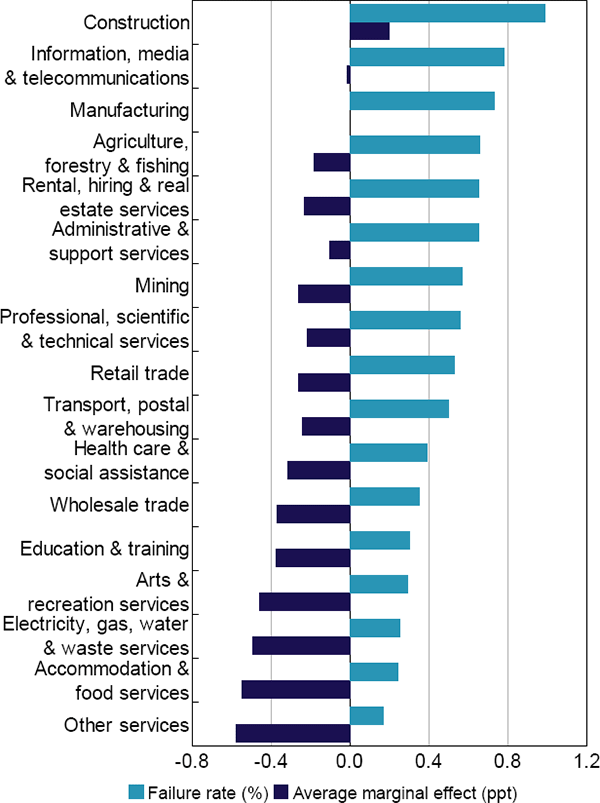
Note: Marginal effects are calculated relative to the manufacturing industry
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
We also find evidence that aggregate conditions matter for the probability of failure, even after controlling for company-level characteristics. This is shown by the estimates of the time fixed effects in the model (the ‘conditional failure probability’ in Figure 7). The observed pattern in the time dummies suggests they represent macroeconomic conditions. For instance, they typically spike during slowdowns, as demonstrated during the 2001 and 2008–09 periods. There is also some evidence of a spike around 2012 and 2013, suggesting that the decline in commodity prices and the fall in mining investment were associated with a relatively high rate of company failure.
A comparison of the average annual failure probabilities (the ‘unconditional failure probability’) and the conditional failure probabilities in Figure 7 highlights the relative contribution of the company-level characteristics in explaining failure. Changes in company-level characteristics have caused a reduction in estimated failure risk over the sample period. The portion of this improvement that occurred between 2007 and 2012 is consistent with the improvement in non-financial corporations' balance sheets over this period (RBA 2016).
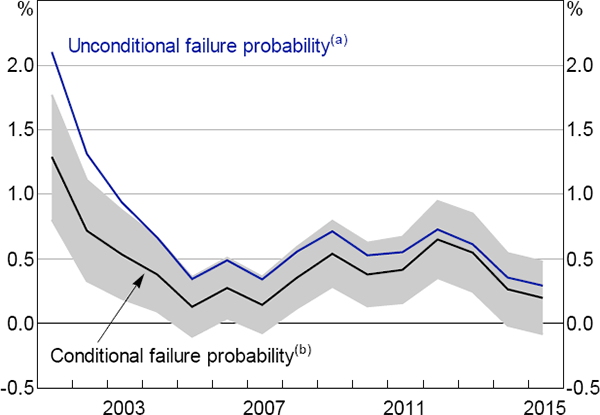
Notes:
(a) Average predicted failure probability in each year
(b) Average marginal effect of the year dummies; 2000 is the base year; shaded area
represents 95 per cent confidence intervals
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
The statistically significant effect of the time dummies is also consistent with the importance of network effects (or ‘ripples of risk’) – the failure of one company during a downturn can lead to the widespread failure of related companies through, for instance, trade credit linkages.
The benchmark model has good explanatory power in that it can adequately distinguish companies that fail from those that do not. This is shown by the estimated area under the receiver operator characteristic (ROC) curve. The area under the ROC curve for a model that perfectly distinguishes failing and non-failing observations is 1. The expected area under the curve for a model that effectively guesses failure probabilities (a model with no information) is 0.5. The area under the ROC curve for the benchmark model is 0.73, which is similar to that for a market-based predictor of listed company failure (Robson 2015).[20] If the time dummies are removed from the model, the estimated area drops only slightly to 0.71. This indicates that structural and cyclical company-level characteristics are sufficient to rank companies in terms of failure risk.
Footnotes
It is also possible that public companies are more focused than private companies on short-term profits and, for listed companies, share price targets, which may lead them to be more myopic and adopt more aggressive growth strategies (Haldane 2011). [18]
Illegal phoenix activity involves the intentional transfer of assets from an indebted
company to a new company to avoid paying creditors, tax or employee entitlements.
The directors leave the debts with the old company, often placing that company into
administration or liquidation, leaving no assets to pay creditors (ASIC 2015).
[19]
Robson also provides a more detailed explanation of the ROC curve. [20]