RDP 2016-09: Why Do Companies Fail? 4. Data
November 2016
4.1 Sample Selection
We construct our sample of companies based on two separate datasets. For both datasets we exclude companies in the financial services industry.[12] The sample period covers the years from 2000 to 2015. The combined dataset is an unbalanced panel as companies drop in and out of the sample due to factors such as failure, mergers and acquisitions.
Data on listed companies come from Morningstar. The listed company data include all domestically domiciled non-financial companies listed on the Australian Stock Exchange. These data are semiannual and cover more than 2,400 companies. The median number of observations per company is 24. Data on unlisted companies are from Dun & Bradstreet (D&B). The D&B panel is based on annual data covering more than 20,000 companies, with a median of about four observations per company.[13]
Overall, the combined dataset comprises more than 90,000 observations on over 23,000 companies. To maximise comparability between the listed and unlisted company samples we estimate the benchmark model using annual data. For more details on the composition of the sample see Table 1.
We identify failed companies in our data using publicly available information on corporate insolvency available from ASIC. These data cover all failed companies and are matched to the sample of companies in the combined dataset for which we have financial statement information.
The D&B sample of companies is based on its primary business as a credit bureau. Companies in the database are likely to be those that applied for credit, and D&B can most easily obtain financial information on relatively large companies, which are required to file their financial reports with ASIC. As a result, compared to the population of all private and unlisted public companies in Australia, the sample is biased towards larger companies, though it does still have some coverage of very small companies (those with revenue less than $500,000).
The slant towards larger companies wanting to borrow does not necessarily undermine the motivation for our work. In fact, the direction of any possible sample selection bias is unclear. To the extent that the sampled companies are relatively large and/or have better access to credit, they may be less likely to fail than the average company in the population as a whole. On the other hand, the sampled companies may be more leveraged than the representative Australian company and therefore more vulnerable to unexpected negative shocks, and hence more likely to fail.
An additional practical challenge is that the exact date at which a company fails is typically known, but the characteristics of the company, such as the state of the balance sheet, are rarely observed at the precise moment of failure. For example, in the Dick Smith case, the company released its last annual report in August 2015 and entered external administration in January 2016. There was at least a six-month period in which the conditions of the company were not transparent to investors, creditors and employees.
It is somewhat surprising how rarely this type of censoring is discussed in the corporate failure literature given its pervasiveness. To address this issue, we adopt a simple form of imputation, which is known as ‘last value carried forward’ (Allison 2010). Under this approach, the company at the moment of failure is assumed to have the financial characteristics that it had in its most recent financial reports. For example, Dick Smith's balance sheet for 2014/15 was known at August 2015 and this information would be carried forward to the year of failure in 2016. We allow financial data to be carried forward by at most one year. If financial data are not observed within one year of a company failing, we do not capture this failure within our sample.[14]
4.2 Model Variables
The benchmark model includes a range of cyclical company-level variables that are fairly standard in the literature on modelling corporate exit. We outline each variable in turn.
Age
We explicitly account for company age (measured as the natural log of the number of years since the company registered with ASIC) in the baseline hazard rate. A consistent research finding is that younger companies are more likely to fail than older companies, presumably due to ‘learning-by-doing’ (e.g. Jovanovic 1982).[15] Because of their limited track records, start-ups typically face restricted access to external finance and are less experienced in developing business models and company strategies.
Size
We include company size (as measured by the natural logarithm of assets) as a key determinant of corporate failure. The existing overseas literature commonly finds that small companies are more likely to fail than large companies (e.g. Hunter and Isachenkova 2006; Bhattacharjee et al 2009).[16] This is presumably because small companies are more likely to be credit constrained, given they have less capacity to raise bank finance and have limited access to non-bank finance (e.g. corporate bonds). Similarly, small companies presumably have less bargaining power with suppliers and creditors, so financing conditions may be more restrictive in terms of business-to-business lending.
Profitability
Profitability is likely to be a key determinant of company failure. We measure profitability as the ratio of earnings before interest and tax to total assets. Higher earnings increase the ability of companies to service their debt payments.
Leverage
Existing research indicates that the level of indebtedness is an important driver of corporate failure (Bunn and Redwood 2003). The link between leverage and default risk is a key component of distance-to-default models (e.g. Robson 2015). Companies that are more leveraged (and hence have less equity) are more vulnerable to asset devaluations. Companies with high leverage also typically have greater debt-servicing burdens and hence are more vulnerable to negative earnings shocks.
We measure leverage in two ways. First, we construct a traditional estimate based on the reported debt-to-assets ratio of each company. This debt includes both bank debt and non-bank debt (e.g. corporate bonds). Second, we construct a more novel estimate based on the level of trade credit (or business-to-business lending) of each company. More specifically, we measure (net) trade credit as accounts payable outstanding (loans from other firms) less accounts receivable (loans to other firms) and we divide this net debt estimate by total assets. We refer to this as the ‘trade credit-to-assets ratio’.
Liquidity
Liquidity is likely to be a key factor determining whether a company remains solvent or not; higher levels of liquid assets allow companies to absorb any unexpected adverse shocks to their balance sheets. We measure liquidity as the ratio of cash (and cash equivalents) to total assets.
Structural characteristics
The model also includes a set of variables that are designed to capture structural characteristics. We include a variable to capture the type of ownership (PUBLIC); the dummy is equal to one when the firm is a public company and is equal to zero when the firm is a private company. Separate to this, we include a dummy variable to indicate whether a public company is listed or not (LISTED). The benchmark model also includes industry fixed effects to capture the possibility that some industries may be inherently riskier than others (e.g. construction and mining).
Before estimation we exclude outliers in some of the company-level variables. First, we exclude observations in which assets, debt or cash are reported to be negative. Second, we exclude observations in which the company holds debt that is more than twice the value of its assets, cash that is more than the value of total assets, and a ratio of earnings to assets that is greater than 10 in absolute terms.[17]
The benchmark model is estimated across the full sample of companies. In an extension, we also estimate separate specifications for the listed and unlisted company sub-samples. This allows us to see whether the determinants of failure vary with the type of ownership. Moreover, these disaggregated models provide additional flexibility in terms of variable choice. For example, the D&B database provides information on subsidiary status for unlisted companies, which is not available for listed companies in the Morningstar database. The listed company model is also estimated on semiannual data rather than annual data which provide more timely information to precisely identify the causes of failure.
4.3 Summary Statistics
Our final sample comprises over 90,000 observations on more than 23,000 companies. Over the whole sample period, 0.6 per cent of company observations are incidents of failure, which is an unconditional estimate of the annual failure rate. And, over the sample period, 2.3 per cent of companies are observed to fail (there are around four observations per company on average). Many non-failing companies are still present in the sample at the end of 2015 (are right censored), but others drop out of the sample before 2015 for a variety of reasons that are not easy to observe (e.g. mergers and acquisitions, voluntary exits and missing data).
The probability of failure varies with company ownership status. On an annual basis, the average rates are 0.75 per cent for publicly listed companies, 0.50 per cent for publicly unlisted companies, and 0.55 per cent for private companies.
The key features of our company-level variables are summarised in Table 1, which splits observations into failing and non-failing observations. In terms of cyclical variables, failing companies are more leveraged, less profitable and less liquid than surviving companies. Failing companies are also generally smaller and younger than the average in our sample.
| Mean | Percentile | Standard deviation | |||
|---|---|---|---|---|---|
| 25th | Median | 75th | |||
| Failures | |||||
| Age (years) | 14.2 | 6.0 | 10.0 | 19.0 | 12.5 |
| Log of age | 2.3 | 1.8 | 2.3 | 2.9 | 0.8 |
| Assets ($m) | 82.2 | 1.4 | 5.3 | 30.0 | 349.5 |
| Log of assets | 1.9 | 0.4 | 1.7 | 3.4 | 2.3 |
| Debt-to-assets ratio (%) | 24.0 | 0.0 | 7.2 | 37.7 | 34.0 |
| Trade credit-to-assets ratio (%) | 7.0 | −0.3 | 0.1 | 12.8 | 28.0 |
| Cash-to-assets ratio (%) | 8.3 | 0.0 | 0.8 | 6.3 | 19.1 |
| Return on assets (%) | −9.1 | −8.0 | 0.0 | 0.0 | 239.7 |
| Observations | 532 | ||||
| Non-failures | |||||
| Age (years) | 19.7 | 8.0 | 15.0 | 26.0 | 17.5 |
| Log of age | 2.6 | 2.1 | 2.7 | 3.3 | 0.9 |
| Assets ($m) | 281.0 | 2.5 | 11.7 | 47.5 | 2,467.4 |
| Log of assets | 2.4 | 0.9 | 2.5 | 3.9 | 2.5 |
| Debt-to-assets ratio (%) | 17.2 | 0.0 | 4.1 | 26.7 | 25.4 |
| Trade credit-to-assets ratio (%) | 1.4 | −5.9 | 0.0 | 6.5 | 24.0 |
| Cash-to-assets ratio (%) | 12.8 | 0.0 | 3.3 | 15.6 | 20.9 |
| Return on assets (%) | 104.2 | 0.0 | 0.0 | 219.1 | 338.3 |
| Observations | 90,197 | ||||
|
Note: Statistics shown are for the sample of companies used in estimation |
|||||
It is also interesting to examine how average failure rates vary across the distributions of some of the key variables. In Figure 2, we construct estimates of the mean failure rate across the distributions of each of the company-specific cyclical indicators, where the distributions of each indicator are divided into deciles.
For some variables, such as the debt-to-assets ratio, the net trade credit-to-assets ratio and the cash-to-assets ratio, it is helpful to separate out company-year observations that are reported to be zero. For these variables, we construct distributions only across the observations reporting nonzero values. The mean failure rates for the company-year observations with zero values are summarised as a separate column indicated by a decile of ‘0’.
The cross-sectional distribution of the return on assets is difficult to represent graphically in a histogram. More than a third of observations have a zero value for return on assets – these observations are all included in the third decile of this distribution. The first and second deciles of this distribution represent company-year observations with a negative return on assets, while the sixth to tenth deciles are observations with positive return on assets.
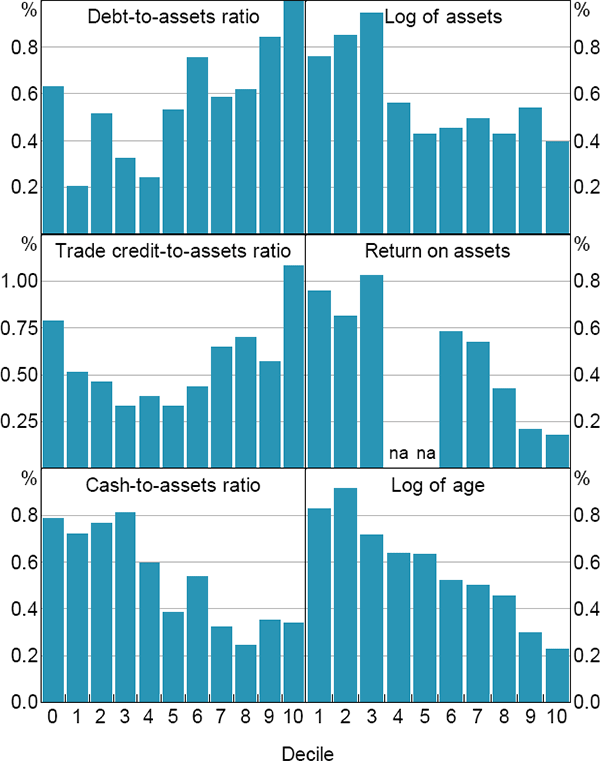
Sources: Australian Securities and Investments Commission; Authors' calculations; Dun & Bradstreet; Morningstar
The histograms indicate that average failure rates are positively correlated with leverage and negatively correlated with size, age, profitability and liquidity. Based on these distributions, we choose a simple specification for the benchmark model and ignore potential non-linearities between the probability of failure and the company-specific cyclical factors.
Footnotes
The determinants of failure are likely to be quite different for financial services companies. For example, a financial institution may be highly leveraged because of the nature of its business (e.g. loan provision) rather than excessive risk-taking. [12]
The unlisted company financial statements are somewhat sporadic in our dataset, even for ‘healthy’ companies; D&B may not collect the financial statements of a company every year, but only every few years. [13]
There are only 100 failures for which we observe financial data in the same year, so 432 of our 532 failures are represented by financial data carried forward from the prior year. [14]
ABS business count data indicate that about half of all start-ups typically survive to the age of 4 years. [15]
ABS business count data indicate that small businesses are about three times more likely to exit than large businesses. [16]
We have experimented with alternative approaches to treating outliers. For example, rather than excluding outliers, we have constructed estimates based on quintiles of the distribution of leverage, profitability and liquidity. Under this approach, a company that reports a debt-to-assets ratio of 1,000 is given the same weight in the regression as a company that reports a debt-to-assets ratio of 1. These results are very similar to those presented in the benchmark model and are available upon request. [17]