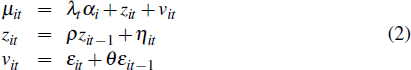RDP 2015-15: Household Economic Inequality in Australia 5. Transitory and Persistent Income Inequality
December 2015 – ISSN 1448-5109 (Online)
- Download the Paper 4.72MB
According to Friedman's (1957) permanent income hypothesis, the distribution of household consumption should closely resemble the distribution of permanent income. So an alternative way to examine how household economic inequality has evolved, and to understand its welfare implications, is to explore whether changes in income inequality have been driven by persistent or transitory shocks to income.
The distinction between persistent and transitory income can be important for a couple of reasons (outlined in DeBacker et al (2013)). First, the distinction may help to understand the determinants of higher annual cross-sectional inequality. For example, if higher inequality is due to more persistent shocks to income, then potential explanations could include structural changes in the labour market and institutional changes that affect employers' remuneration policies. If, instead, higher inequality is due to temporary income fluctuations, then this could reflect changes in factors such as job mobility, workplace flexibility or the development of a bonus culture. Second, the distinction helps to inform welfare evaluations of changes in inequality. A change in income inequality that persists over time will have a larger welfare effect than a change in income inequality that is only temporary, especially if there are no constraints on households that prevent them from smoothing their consumption.
To separately identify the persistent and transitory income shocks driving inequality, we need to be able to track individual households over time. The HES surveys a different cross-section of households every time, so it is not useful for this. Instead, to explore the dynamics of household income, we turn to longitudinal household-level data from the HILDA Survey.
Our analysis takes two separate approaches to investigate household income dynamics. We first adopt an error components model to fully specify the process that generates income over time and decompose income into a highly persistent component and another transitory component that allows for some (limited) serial correlation. We then present estimates of income mobility as another way to consider dynamic changes in income using a household panel.
The HILDA Survey data cover the period from 2001 to 2013. The main income measure used is real annual household disposable income. This measure is population weighted and divided by an equivalence factor to control for household size and composition to make the estimates as consistent as possible with those obtained using the HES data. Households must be present for at least three consecutive years of the survey, and those with non-positive income and missing demographic information are excluded from the sample. The final sample consists of about 19,000 households and almost 100,000 observations.
Based on the HILDA Survey, there has been a trend increase in income inequality. Between 2001 and 2013, the share of aggregate disposable income held by the top 1 per cent of highest-earning households rose from 4.6 per cent to nearly 6 per cent. The top 10 per cent of earners saw their share of aggregate income rise from 22.7 per cent to 25 per cent over the same period. This is consistent with the trend increase in income inequality observed in the HES data over the 2000s. For most of the analysis in this section of the paper it is more useful to work with a measure of inequality based on the variance of household disposable income. The variance of income increased by about 8 log points between 2001 and 2013.
To quantify the extent to which the rise in income inequality is due to persistent and transitory factors, we first estimate the portion of inequality explained by observed differences across households using the following least squares regression:
where the dependent variable is the log of equivalised household disposable income (ln(Yit )) and the set of explanatory variables (Xit) includes the characteristics of the household head, such as level of education, gender, age, employment status, migrant status, indigenous status, and marital status. The specification also includes state, occupation and industry fixed effects, as well as interaction terms for occupation with industry and state variables. The regressions are estimated separately for each year in the sample.
We then take the estimated residuals (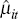 )
from Equation (1) for each household i in year t and calculate
the variance of these residuals each year. We plot this variance, which we
label ‘residual’ income inequality, together with total and explained
income inequality in Figure 13. We define ‘explained’ inequality
as the variation in income over time explained by the observable household
characteristics included in the set of explanatory variables (Xit).
)
from Equation (1) for each household i in year t and calculate
the variance of these residuals each year. We plot this variance, which we
label ‘residual’ income inequality, together with total and explained
income inequality in Figure 13. We define ‘explained’ inequality
as the variation in income over time explained by the observable household
characteristics included in the set of explanatory variables (Xit).
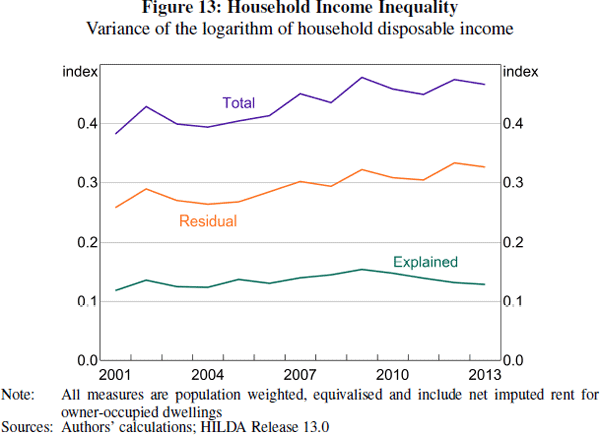
Looking at changes over time, we find some evidence that the rise in income inequality between 2001 and 2009 was due to changes in observable characteristics. But most of the rise in inequality cannot be explained by observed inequality. Instead, on average, residual inequality accounts for about 70 per cent of total income inequality. Residual inequality bears a close resemblance to total inequality, with the two estimates displaying similar upward trends and short-term fluctuations. This suggests that observable factors, such as an ageing population and rising educational attainment, have played limited roles in explaining changes in inequality over the past decade and the unobserved, dynamic component of income has been the main determinant of rising income inequality.
5.1 Error Components Model
We next use an error components model (ECM) to decompose residual income inequality. The ECM has been standard in the inequality literature since Gottschalk and Moffitt (1994). Many international studies have used this model to estimate the dynamics of inequality over time, particularly for the United States using the Panel Study of Income Dynamics Survey.[15] To date, this approach has not been possible for Australia due to the absence of a sufficiently long panel dataset.
To address this, we use the panel structure of the HILDA Survey and a flexible specification of the ECM to examine the dynamics of household income inequality for Australia.
As before, the residual of log equivalised disposable income for household i in year t is estimated from the regression described by Equation (1). The dynamics of the residual are then modelled by the following process:
where the ‘persistent’ component of inequality is a combination of a
household fixed effect (αi) that has a time-varying coefficient (λt),
with total variance of 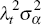 , and a highly persistent term (zit)
that follows an autoregressive AR(1) process and has variance of
, and a highly persistent term (zit)
that follows an autoregressive AR(1) process and has variance of 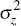 . The household fixed
effect captures unobserved time-invariant factors such as skill or ability
(i.e. human capital). The time-varying coefficient captures the ‘market
price’ for human capital. The AR(1) term (zit) captures
other shocks to income that persist over time, such as promotions that affect
the level of wage income or possibly a long-term health condition. The temporary
component (νit) is specified as a moving average MA(1)
process. This specification allows temporary income factors, such as lay-offs
and bonuses, to have effects that persist for more than a year. This is motivated
by empirical observation of the autocovariances of household income in the
HILDA data.
. The household fixed
effect captures unobserved time-invariant factors such as skill or ability
(i.e. human capital). The time-varying coefficient captures the ‘market
price’ for human capital. The AR(1) term (zit) captures
other shocks to income that persist over time, such as promotions that affect
the level of wage income or possibly a long-term health condition. The temporary
component (νit) is specified as a moving average MA(1)
process. This specification allows temporary income factors, such as lay-offs
and bonuses, to have effects that persist for more than a year. This is motivated
by empirical observation of the autocovariances of household income in the
HILDA data.
The ηit and εit terms are the
respective persistent and transitory shocks to income with mean zero and time-varying
variances, 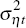 and
and 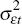 ,
respectively. These shocks are assumed to be uncorrelated with each other and
independently and identically distributed across households over time. Under
this error scheme, changes in residual inequality can be driven by changes
in three different factors: 1) the variance of persistent shocks; 2) the variance
of temporary shocks; and/or 3) changes in the market price of a household's
fixed human capital.
,
respectively. These shocks are assumed to be uncorrelated with each other and
independently and identically distributed across households over time. Under
this error scheme, changes in residual inequality can be driven by changes
in three different factors: 1) the variance of persistent shocks; 2) the variance
of temporary shocks; and/or 3) changes in the market price of a household's
fixed human capital.
We estimate the variance-covariance matrix of the model using generalised method of moments. This procedure essentially estimates a parameter vector of interest by minimising the weighted sum of squared distances between the population moments implied by the model and their empirical counterparts. The parameter vector is then used to construct estimates of the variances of transitory and persistent shocks to income, and the variance of the return to fixed human capital, shown in Figure 14.
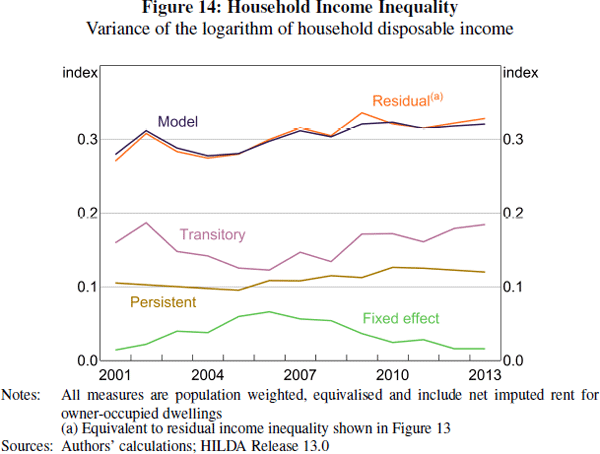
Our preferred estimates indicate that about two-thirds of the level of residual inequality is due to the variance in transitory income shocks. Given that about 70 per cent of the variation in total income across households is due to unobserved characteristics, this suggests that temporary shocks explain close to one-half of the total cross-sectional variation in household income. The remaining variation in income across households is mainly due to variation in persistent shocks, though some inequality is also explained by variation in unobserved fixed human capital.
The model also indicates that the first half of the sample period (2001 to 2006) was characterised by a slight decline in transitory income inequality and a small (and largely offsetting) increase in persistent income inequality (due to an increase in the variance of the fixed effect). This appears to reflect developments in the Australian labour market over that period. In particular, the unemployment rate fell noticeably between 2001 and 2006 and this is likely to have disproportionately benefited lower-income workers who may be more exposed to temporary income shocks. The increase in the variance of the fixed effect in the early to mid 2000s reflects a rise in the ‘price’ that the market was willing to pay for unobserved ability, which may also be due to the relatively strong labour market at the time.
The trend in overall income inequality in the latter half of the sample period appears to reflect an increase in the variance of both transitory and persistent income shocks. There also appears to be a slight jump in transitory income inequality around the time of the global financial crisis. This suggests that the crisis had a limited effect on the distribution of consumption across households. In general, households are more able to insulate their consumption from transitory rather than persistent shocks to income. The slight rise in the variance of persistent income shocks since the middle of the 2000s is consistent with the small increase in consumption inequality reported in the HES over a similar period.
5.2 Income Mobility
To further quantify the extent to which the trends in inequality are persistent we next estimate the degree of mobility in the income distribution. Income mobility has a direct bearing on the degree of persistence in inequality. For example, if household income is relatively immobile and the same households are ranked as high-income from one year to the next, then this suggests that the inequality is persistent. In contrast, if household income is fairly mobile on average then high-income households may move down the income rankings the following year, suggesting that the inequality is temporary.
To examine mobility, we divide the sample into quintiles based on the residual income estimates. We then estimate the share of households that move up, down or stay in the same quintile over time. We do this for both 1-year and 10-year windows to measure short-term and long-term mobility.
| Income quintile | From t to t+1 | From t to t+10 | ||||
|---|---|---|---|---|---|---|
| Down | Same | Up | Down | Same | Up | |
| Lowest | 58 | 42 | 46 | 54 | ||
| 2nd | 23 | 38 | 39 | 24 | 27 | 49 |
| 3rd | 33 | 34 | 32 | 38 | 23 | 39 |
| 4th | 40 | 37 | 23 | 50 | 26 | 25 |
| Highest | 41 | 59 | 55 | 45 | ||
|
Sources: Authors' calculations; HILDA Release 13.0 |
||||||
Just over half of households that are either in the top or bottom income quintile remain in that same quintile from one year to the next (Table 1). More notably, a bit over 40 per cent of these households are in the same quintile a decade later.[16] For households in the middle income quintiles, about a third change quintiles each year and about a quarter are in the same quintile a decade later. This evidence suggests that both persistent and transitory movements are occurring within the income distribution over time, though there is some variation across income quintiles.[17]
To directly quantify the extent to which the observed mobility reflects permanent or temporary transitions we use a key indicator of income mobility – the Shorrocks R index (Shorrocks 1978). This index provides a direct link between mobility and the relative contribution of persistent and transitory inequality by defining immobility as the ratio of persistent inequality to average annual or total inequality over the same period. The Shorrocks R index is defined as:
where the numerator, I[Y], is a multi-year inequality value estimated from household
incomes aggregated over
T years; the denominator is the weighted average of single-year
inequality values, I[Yt], over the T-year
period. The weight assigned to each year, wt = 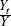 , is the ratio of average
household income in year t (Yt) to average total
household income (Y) earned over the entire period.
, is the ratio of average
household income in year t (Yt) to average total
household income (Y) earned over the entire period.
The Shorrocks R index reflects the relative contribution of persistent to total income inequality over time. The index can take values between 0 and 1. The higher the value of the index, the higher the share of persistent or long-term inequality, and the less mobility there is in the income distribution.
To calculate the index, it is necessary to use an inequality measure, I[Y], that is a strictly convex function (Shorrocks 1978). We use two common inequality indices that meet this condition to estimate mobility for both total and residual household disposable income – the Theil index and the Gini coefficient.[18]
To assess whether the share of persistent inequality (or income immobility) has changed over time, we divide the HILDA panel into moving 5-year windows and estimate the Shorrocks R value for each sample window.
Based on the Theil index, the Shorrocks R value remains relatively stable over the nine 5-year windows spanning 2001 to 2013, with average R values for total and residual household disposable income of 0.81 and 0.70, respectively (Table 2).[19]
| Year | Theil index | Gini coefficient | |||
|---|---|---|---|---|---|
| Total | Residual(a) | Total | Residual(a) | ||
| 2001–2005 | 0.80 | 0.70 | 0.91 | 0.85 | |
| 2002–2006 | 0.79 | 0.70 | 0.91 | 0.85 | |
| 2003–2007 | 0.79 | 0.69 | 0.91 | 0.85 | |
| 2004–2008 | 0.78 | 0.69 | 0.91 | 0.84 | |
| 2005–2009 | 0.79 | 0.70 | 0.91 | 0.85 | |
| 2006–2010 | 0.84 | 0.71 | 0.93 | 0.86 | |
| 2007–2011 | 0.87 | 0.74 | 0.94 | 0.87 | |
| 2008–2012 | 0.83 | 0.72 | 0.93 | 0.87 | |
| 2009–2013 | 0.79 | 0.68 | 0.91 | 0.85 | |
|
Note: (a) Residual income estimated using Equation (1) Sources: Authors' calculations; HILDA Release 13.0 |
|||||
However, we do observe a slight rise in the share of persistent inequality or immobility from the middle of the 2000s onwards, with higher R values reported for the second half of the sample period.[20]
This increase in persistent inequality is consistent with the rise in the variance of persistent shocks observed in Figure 14 over the same period, as well as the small increase in consumption inequality reported in the HES between 2003/04 and 2009/10.
Footnotes
Prominent examples include MaCurdy (1982), Abowd and Card (1989), Blundell, Pistaferri and Preston (2008) and Heathcote et al (2010). [15]
The results reported in Table 1 are robust to using a balanced panel and a sample of working-age households. [16]
The skew in the income distribution could account for some of the differences in estimated mobility across the income quintiles. The positive skew implies that there is greater dispersion in income within the top income quintile than in any of the lower quintiles. This implies, for example, that a negative income shock of a particular size will be more likely to cause a given household to fall out of the second highest quintile than out of the highest quintile, all other things being equal. [17]
The Theil index is defined as 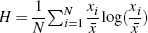 where xi is the income of household i and
where xi is the income of household i and 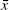 is mean household income. This index measures the distance the population
is away from perfect equality. If all households have the same income, then
the index is equal to 0, signalling perfect equality. If one household has
all the income, then the index is equal to 1, implying perfect inequality.
The Gini coefficient is defined in Section 3.1.
[18]
is mean household income. This index measures the distance the population
is away from perfect equality. If all households have the same income, then
the index is equal to 0, signalling perfect equality. If one household has
all the income, then the index is equal to 1, implying perfect inequality.
The Gini coefficient is defined in Section 3.1.
[18]
The estimated degree of persistent inequality appears to be lower for Australia than for some other advanced economies based on the Theil index. For instance, Bayaz-Ozturk, Burkhauser and Couch (2014) report Shorrocks R values of 0.83 and 0.85 for the United States and Germany over the late 1990s to early 2000s. [19]
The same pattern is observed for the Gini coefficient, although the Gini coefficient typically reports higher values for R than other inequality measures that place weight on the extremes of the income distribution (Jarvis and Jenkins 1998). [20]