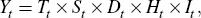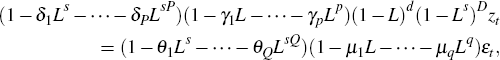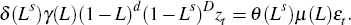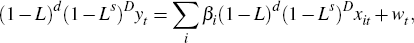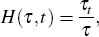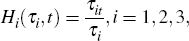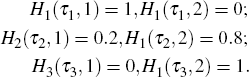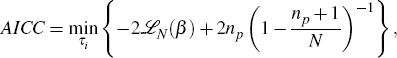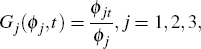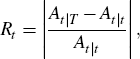RDP 2015-13: Seasonal Adjustment of Chinese Economic Statistics 2. Seasonal Adjustment with Chinese Moving Holiday Effects

This section gives an overview of the X-12-ARIMA and SEATS (Signal Extraction in ARIMA Time Series) approaches, and how they can be used to adjust data affected by the Chinese New Year and other moving holidays. To implement seasonal adjustment with these approaches we use the X-13-ARIMA-SEATS package, which employs an automatic model selection procedure based on that of the TRAMO (Time Series Regression with ARIMA Noise, Missing Observations and Outliers) program (Gómez and Maravall 1996).

These procedures assume a seasonal decomposition along the following lines:

where the time series, Y_t, is a multiplicative combination of five unobserved components: trend (or trend-cycle), T_t; seasonal, S_t; trading day, D_t; holiday, H_t; and irregular, I_t. The trading day and holiday components represent calendar effects: trading day effects are related to the number of days and the number of working days in a month, while holiday effects are related to moving holidays such as Chinese New Year. The irregular component is a residual that combines all fluctuations not covered by the other components in the decomposition.^[4]

Both the X-12-ARIMA and SEATS procedures first implement a pre-adjustment stage which estimates corrections for Chinese New Year and/or other moving holidays. When the data have been extended in both directions to help mitigate end-point problems, and cleaned of outliers and deterministic calendar effects (Section 2.1), they are fed into a seasonal adjustment procedure (Sections 2.2–2.3) that undertakes the decomposition of the cleaned series into trend, seasonal and irregular components. Finally, the outliers that were removed in the pre-adjustment stage are reintroduced into the seasonal or trend components (depending on the type of outlier), the holiday and trading day components are reincorporated, and diagnostics can be applied to assess the quality of the seasonal adjustment (Section 2.4)

2.1 ‘Pre-adjustment’ and Correcting for Chinese New Year

The first step of the pre-adjustment is to extend the time series in both directions to reduce end-point problems and minimise revisions. In the process, a selection of dummy variables are used to purge the data of calendar effects. Also in this stage, an outlier detection algorithm is employed to identify and remove outliers.

2.1.1 ARIMA modelling

For the time series of interest, Y_t, define a process

where X_t is a vector of regressors to model calendar-related effects. It includes dummy variables to control for trading day effects, outliers and moving holidays (including Chinese New Year). Because the errors, z_t, are unlikely to be stationary and will most probably be autocorrelated, they are modelled using a zero mean, multiplicative seasonal ARIMA model to allow for the possibility that Y_t is integrated at seasonal lags.

The process for z_t is specified as a seasonal ARIMA (p, d, q)(P, D, Q):

where L is a lag operator. For monthly data s = 12; for quarterly data s = 4; p and q are lag orders of the AR and MA parameters for the non-seasonal ARIMA; P and Q are lag orders of the AR and MA parameters for the seasonal ARIMA; d and D are orders of, respectively, non-seasonal and seasonal integration; and ε_t is a normal, independently and identically distributed random variable.

This expression can be simplified to:

The model can also be expressed as follows:

where w_t follows a stationary ARMA process.

This model can be estimated by maximum likelihood. The model selection process is automated and done in several stages. Initially, an ARMA model is estimated, and outlier identification and tests for the significance of calendar effects are performed (see Appendix B for details). Next, unit root tests are used to determine the order of differencing. Then, an iterative process is applied to determine the lag order of ARMA parameters. The lag orders of the seasonal part of the ARIMA model are chosen by minimising an information criterion.^[5]

A similar procedure is then applied to obtain the lag orders of the non-seasonal part of the ARIMA model. The chosen ARIMA model is then compared with a default ARIMA(011)(011) model; if the chosen model is found to display a lower information criterion than the default model, regressors for calendar effects and tests for outliers are reapplied, and a final model is selected.

2.1.2 Adjusting for the Chinese New Year holiday

Our approach to adjust for Chinese New Year uses the moving holiday regressor of Bell and Hillmer (1983). In its simplest version, this approach defines a dummy variable

where t is the month in which part of Chinese New Year falls, τ_t is the number of days affected by Chinese New Year in month t, and τ is the total number of holiday-affected days. The dummy variable is equal to the fraction of holiday-affected days that fall in each month. It has differential quantitative impacts in the months of January and February, depending on the number of days of the holiday that fall in each.

An alternative three-sub-period version employed by Lin and Liu (2003) takes the form:

where it is the month in which part i of the period affected by Chinese New Year falls, τ_it is the number of days affected by part i of Chinese New Year in month t, and τ_i is the total number of holiday-affected days in part i of Chinese New Year. Effectively, the January–February period is partitioned into three sub-periods in which the holiday is assumed to have differential effects: the sub-period leading up to the holiday, the sub-period during the holiday and the sub-period after the holiday. The dummy for each sub-period is equal to the fraction of holiday-affected days in that sub-period that fall in each month.

Figure 3 illustrates how moving holiday regressors can be used to remove the effect of Chinese New Year, based on one particular example. In the figure:

Allowing the effect of Chinese New Year to be absorbed by three dummy variables rather than one increases the flexibility with which the effect can be modelled. In the example, the eve of Chinese New Year is assumed to fall on 31 January, and each of the three sub-periods is assumed to have a length of five days. Unfortunately, the literature provides little guidance regarding the length of the sub-periods to which each dummy variable corresponds. Lin and Liu (2003) assume that τ_i = τ for each H_i. But there is no reason to assume that the number of days affected by Chinese New Year in each sub-period is the same. In principle, the number of days in each sub-period (τ₁,τ₂,τ₃) can be allowed to vary according to the characteristics of the individual time series.

Lin and Liu (2003) follow the suggestion of Findley and Soukup (2000) that the selection of τ be chosen by finding the model that minimises an Akaike information criterion (AIC), corrected for finite sample sizes – namely, the AICC of Hurvich and Tsai (1989):

where ℒ_N(β) is the maximised log likelihood function with parameters β, evaluated over N observations, and n_p is the number of parameters.^[6] The reason for this approach is that the models with different τ are not nested and, therefore, model selection cannot proceed on the basis of standard likelihood ratio tests.

To extend the approach of Lin and Liu (2003), we propose that the lengths of the three sub-periods be optimised for each individual time series. The method is straightforward: for any given series, we estimate a seasonal ARIMA model for each possible combination of sub-period lengths: (2,2,2), (2,2,3), … (2,2,T), …, (2,3,2), … (2,T,2), …, (3,2,2), …, (T,2,2), …, (2,T,T), (3,T,T), … (T,T,T). We impose a maximum sub-period length of T = 20.^[7] We then select the combination of window lengths (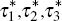) that minimises the AICC.

2.1.3 Adjusting for additional moving holidays

Once a specification of Chinese New Year adjustments has been decided by the above procedure, we implement a similar approach to adjust for the Dragon Boat (May–June) and Mid-Autumn (September–October) festivals. We define

where jt is the month in which part j of the period affected by a given festival falls, ϕ_jt is the number of days affected by part j of the holiday in month t, and ϕ_j is the total number of holiday-affected days in part j of the festival. The May–June (or September–October) period is partitioned into three sub-periods such that the dummy for each sub-period is equal to the fraction of holiday-affected days in that sub-period that fall in each month. We apply the same optimisation method as that described above to determine the sub-period lengths. However, as the Dragon Boat and Mid-Autumn festivals usually last for three days, compared with seven days for Chinese New Year, we impose a shorter maximum sub-period length of ten days.

2.1.4 Outlier detection and removal

When an ARIMA model has been estimated, and all moving holiday corrections have been applied, the residuals are used to identify candidate outliers, using a method based on the outlier detection strategy of Chang, Tiao and Chen (1988). Details are provided in Appendix B. When outliers have been identified, the ARIMA model is re-estimated with appropriate dummy variables included in the X_t vector. This procedure is iterated until no additional outliers are found.

2.2 The X-12 Seasonal Filters

The X-12 procedure is a non-parametric algorithm that iterates between estimates of the trend and seasonal components, using pre-defined filters to smooth seasonal fluctuations from the data. A stylised description of the X-12 filters is given in Appendix B.^[8] When the time series has been pre-adjusted (including for Chinese New Year, trading days and outliers, and forecasted and backcasted), the seasonal adjustment procedure can be implemented. In the final stage, the trend, seasonal and irregular components are combined with additional deterministic components (including Chinese New Year and trading day effects) removed in the ARIMA modelling stage.

2.3 SEATS

Unlike the X-12-ARIMA procedure, which applies pre-defined filters to the pre-adjusted data from the ARIMA stage, the SEATS procedure conducts a direct signal extraction using the ARIMA model to decompose the data into trend, seasonal and irregular components (see Appendix B). The decomposition assumes that these components are orthogonal, and that no white noise can be extracted from a component that is not the irregular one (Gómez and Maravall 1996). The trend and seasonal components are defined to account for the permanent characteristics of the series – that is, the spectral peaks at the origin and at seasonal frequencies – while the irregular component should be white noise or a low order moving average process (Burman 1980; Pollock 2002).

The SEATS program applies the signal extraction procedure described by Burman (1980), which applies a Wiener-Kolmogorov-type filter to the original series and yields minimum mean square error estimators of the three components. At the final stage, as in the X-12-ARIMA procedure, these three components are modified to reintroduce the deterministic effects removed in the ARIMA modelling step.

2.4 Diagnostic Tests

We use standard diagnostic tests to assess the quality of our seasonal adjustment (see Appendix B for a description). To determine whether moving holiday dummies specified to capture Chinese New Year effects are jointly significant, a chi-squared test is used. For all series, we conduct separate significance tests for Chinese New Year, the Dragon Boat festival and the Mid-Autumn festival respectively. If the dummy variables corresponding to a given moving holiday are insignificant, they are dropped.

Assuming that seasonality is present, assessing the quality of a given seasonal adjustment can be difficult. As noted by Bell and Hillmer (1984), all adjustment procedures involve a degree of arbitrariness in establishing a seasonal decomposition. One widely used criterion is due to Nerlove (1964, p 262), who defines seasonality as ‘that characteristic of a time series that gives rise to spectral peaks at seasonal frequencies’. The spectrum may be estimated parametrically by plugging in estimated coefficients from a time series model (see Monsell (2009) for further details). Informal visual inspection of spectral plots can be used to determine if spectral peaks at seasonal frequencies are removed by the various seasonal adjustment procedures.

Another criterion that we consider is the sensitivity of the seasonal adjustment to changes in sample. To do this, we consider robustness to revisions by seasonally adjusting each series over successively increasing time series intervals and averaging absolute percentage revisions for each month, and overall. The percentage revision of the seasonally adjusted series is defined as:

where A_t\n is the seasonal adjustment of the series y₁,y₂,…,y_n for t ≤ n ≤ T, and the final adjustment of observation t is A_t|T.

‘Sliding spans’ analysis (Findley et al 1990) involves comparing seasonal adjustments for overlapping spans of a given time series. Typically, four overlapping spans are considered. For each month of the calendar year, percentage differences across spans for the seasonally adjusted series and its month-on-month changes are calculated. A range of metrics and rules of thumb have been devised to analyse sliding spans (see Findley et al (1990)). In this paper, we focus on the distribution (maximum, minimum and central tendency) of month-on-month changes to help assess the sensitivity of our benchmark seasonal adjustments.

Footnotes

An additive decomposition may be used as well but the multiplicative version is more common in practice. As observed by Dagum (1976), the multiplicative model will deliver an ineffective seasonal adjustment if the data-generating process of the seasonal component is additive. A multiplicative model is appropriate when the magnitude of the seasonal effect is affected by the level of economy activity. Visual inspection suggests that this is the case for the time series considered in this paper. [4]

Similar to the TRAMO procedure, X-13-ARIMA-SEATS minimises a variant of the Bayesian information criterion. [5]

The maximised log likelihood is given by

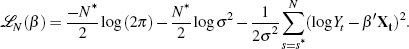
View MathML [6]

Our experiments suggest that the results do not change substantially with higher T. [7]

The X-12 method represents an evolution from various earlier seasonal adjustment techniques developed by the United States Bureau of the Census, including the X-11 method (Shishkin, Young and Musgrave 1967). It has been refined over the years, including through the development of X-11-ARIMA by Statistics Canada in the 1970s (Dagum 1975). Bell and Hillmer (1984) provide an historical overview. [8]