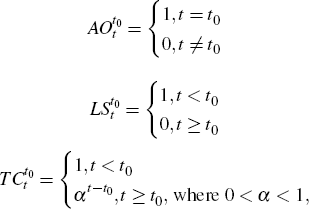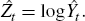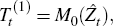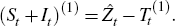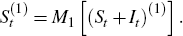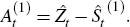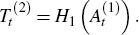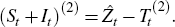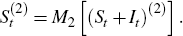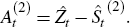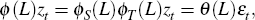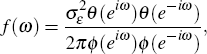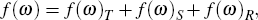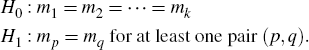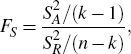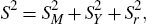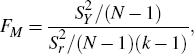RDP 2015-13: Seasonal Adjustment of Chinese Economic Statistics Appendix B: Outlier Corrections, Seasonal Filters and Diagnostic Tests
November 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.18MB
This appendix provides additional details on correcting for outliers in X-12-ARIMA, a general description of the X-12 and SEATS filters, and details of diagnostic tests used in the procedure.
B.1 Outlier Detection and Removal
In the X-13-ARIMA-SEATS package, a method based on the outlier detection strategy of Chang et al (1988) is used to correct for outliers.[22] Typically three types of outliers are defined:
where additive outliers (AO) alter the level of the series temporarily for one period only; level shifts (LS) shift the level permanently; and trend corrections (TC) shift the level at a point in time and have a decaying effect thereafter.
Outliers falling into these categories are defined by calculating test statistics for each time point and outlier type (given constant AR and MA parameters). These are compared to a table of critical values. When outliers have been identified, the ARIMA model is re-estimated with appropriate dummy variables included in the Xt vector. This procedure is iterated until no additional outliers are found. In the final stage of the seasonal adjustment procedure, additive outliers are reincorporated into the seasonal component, while level shifts and trend corrections are reincorporated into the trend component of the series.
B.2 The X-12 Seasonal Filters
Define the fitted values of Equation (1), which exclude the trading day (Dt) and holiday (Ht) components of a series, as:[23]
The trend is initially estimated using a 2 × 12 moving average (which preserves linear trends and eliminates order-12 constant seasonalities)[24]
which is then used to calculate the detrended series (often called the ‘SI ratio’)
The first iteration of the seasonal component is then estimated as a 3 × 3 moving average (which preserves linear trends), over each monthly observation of the combined seasonal and irregular components[25]
This series is normalised to 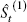 so that the sum of seasonal factors over a 12-month period is approximately zero.
so that the sum of seasonal factors over a 12-month period is approximately zero.
The first estimate of the seasonally adjusted series is:
In the next stage of the algorithm, a second estimate of the trend is formed by applying a Henderson moving average[26] to the initial estimate of the seasonally adjusted series:
The second iteration of the seasonal-irregular component is then given by:
The seasonal component is estimated using a 3 × 5 moving average over each month (which preserves linear trends):[27]
Finally, the seasonal factors are normalised again, resulting in another estimate of the seasonally adjusted series:
The entire procedure is then iterated two more times with minor variations.[28]
B.3 The SEATS Seasonal Filter
In broad terms, seasonal adjustment in SEATS is undertaken as follows. We can rewrite Equation (1) as:
where ϕS(L) contains the seasonal autoregressive factors and ϕT(L) contains the non-seasonal factors.
The population spectrum of the ARIMA(p,d,q)(P,D,Q) will take the general form:
where ω ∈ [0,π].
Under certain assumptions (see Pollock (2002)), the autocovariance generating function for the ARIMA model can be decomposed into three components corresponding to the trend, seasonal and irregular. The estimated ARIMA model provides a way of parameterising the spectrum of the time series, so that a (pseudo) spectral decomposition can be achieved:
where f(ω)T, f(ω)S and f(ω)R refer to the trend, seasonal and irregular components.
B.4 Diagnostic Tests
The test statistics used in this paper are all relatively standard in seasonal adjustment analysis.[29] The first is a test of whether the monthly (or quarterly) means of the detrended series (that is, the SI ratio) are equal. It tests the hypothesis that there is no seasonality:
Assuming that the values of the seasonal factors are independently distributed as normal with means mi and a common standard deviation, one test statistic is:
which follows an F-distribution with k − 1 and n − k
degrees of freedom (Ladiray and Quenneville 2001, pp 57, 135). This test is
based on a one-way analysis of variance, where S2 (the
total sum of squares) is decomposed into 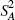 , the variance of the
averages due to seasonality, and
, the variance of the
averages due to seasonality, and 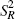 , the residual variance.
, the residual variance.
A second test aims to determine the presence or otherwise of moving seasonality through a two-way analysis of variance. Variation in the detrended series is decomposed into inter-month, inter-year and residual components:
where S2 is the total sum of squares, 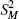 is the inter-month
sum of squares,
is the inter-month
sum of squares, 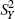 is the inter-year sum of squares and
is the inter-year sum of squares and 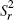 is the residual sum of squares. An F-test is used to test the null hypothesis
that there is no change in seasonality across the complete years of the sample:
is the residual sum of squares. An F-test is used to test the null hypothesis
that there is no change in seasonality across the complete years of the sample:
where N is the total number of years, and FM follows an F-distribution with (N − 1) and (k −1)(N − 1) degrees of freedom.[30]
Footnotes
It is important to correct for moving holidays prior to outlier detection. Otherwise, for example, the January and February observations in Chinese time series will typically be marked as outliers due to the outsized impact of Chinese New Year. [22]
This description of the X-12 filters is largely derived from the comprehensive exposition of the X-11 method by Ladiray and Quenneville (2001). [23]
The so-called 2 × 12 moving average has coefficients 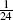 {1,2,2,2,2,2,2,2,2,2,2,2,1}.
[24]
{1,2,2,2,2,2,2,2,2,2,2,2,1}.
[24]
The 3 × 3 moving average has coefficients 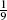 {1,2,3,2,1}.
[25]
{1,2,3,2,1}.
[25]
The purpose of applying a Henderson moving average is to improve the smoothness of the trend and preserve a locally polynomial trend of degree 23. [26]
The 3 × 5 moving average has coefficients 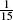 {1,2,3,3,3,2,1}.
[27]
{1,2,3,3,3,2,1}.
[27]
The above description incorporates a slight modification of the actual X-12 procedure. In addition to the outlier detection techniques used in the ARIMA step, the X-12 algorithm has its own automated ‘extreme value’ detection, which is applied repeatedly in successive iterations of the procedure. Essentially, the extreme value detection procedure applies error bands around the irregular component and down-weights observations that fall within a certain number of standard deviations of the mean. This effectively smooths the series further. Our own experiments replicating X-12-ARIMA for Chinese data suggest that the seasonal adjustment of Chinese time series is little changed if this feature is ‘turned off’ by setting the tolerance limits for extreme value detection to very high numerical values. [28]
Simulations by Lytras et al (2007) suggest that the power of these tests is highly variable across different ARIMA models, and in some cases rather low. [29]
A test statistic reported by X-12-ARIMA (‘M7’) that combines the two
F-tests is a test for the presence of ‘identifiable seasonality’
attributable to Lothian and Morry (1978):
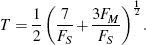
View MathML
[30]