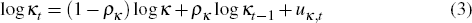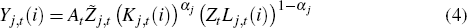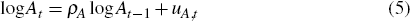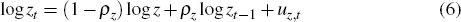RDP 2015-11: Unprecedented Changes in the Terms of Trade 2. Model

We extend a standard small open economy model with nominal rigidities by including capital accumulation as well as non-tradeable and commodity-exporting sectors. Like Rabanal (2009), we include trends in sector-specific productivity processes that give rise to relative price changes in steady state. Since the model is large, in this section we provide a descriptive overview and highlight the treatment of two important features – the behaviour of commodity prices and trends in sectoral productivity. Readers interested in the technical details of the model can refer to Appendix A for a comprehensive presentation.

2.1 The Environment

The model features two economies – a small economy (Australia) and a large economy (the rest of the world). Economic developments in the large economy affect the small economy. But developments in the small economy do not affect the large economy.

The key economic units in the small economy are firms and households. There are four types of firms in the small economy: non-tradeable, non-commodity tradeable, commodity and importing firms. Non-tradeable, non-commodity tradeable and commodity firms produce goods and services domestically using capital and labour as production inputs. Non-tradeable firms sell their output exclusively to households in the small economy. Non-commodity tradeable firms sell their output to households in the small economy and overseas. And commodity firms produce resource commodities for sale overseas. Importing firms sell goods and services produced overseas to households in the small economy. Non-tradeable, non-commodity tradeable and importing firms sell differentiated goods. These firms enjoy some pricing power in the marketplace, which is a monopolistically competitive environment. In contrast, the commodity sector is perfectly competitive.

Households derive utility from consumption and disutility from work. Labour is mobile across sectors, although households view employment in different sectors as imperfect substitutes. Household saving takes the form of bonds denominated in either domestic or foreign currency and capital which, once installed, is specific to each of the three production sectors. Households prefer to smooth consumption over time. To achieve this, when making consumption decisions, households take account of their expected future income stream. An implication of this is that the response of consumption to changes in income will depend upon the expected persistence of those changes. These differences help us to distinguish between permanent and temporary shifts in commodity prices.

We include a number of frictions in the model. In particular, we introduce price stickiness in the form of quadratic adjustment costs that firms must pay when changing their prices as well as quadratic investment adjustment costs. These frictions help the model to capture empirical regularities in Australian macroeconomic data. They also imply that firms will typically adjust prices and capital by less in response to economic disturbances that they expect will be transitory than they do in response to disturbances that they expect to be persistent. As was the case for consumption, the differing responses of prices and investment to short- and long-lived disturbances help us to identify permanent shifts in long-run commodity prices.

2.2 Commodity Prices

Commodity producers operate in an environment of perfect competition, meaning that they take prices as given. These prices are set in world markets and are unaffected by economic developments in the small economy. The price of commodities in foreign currency terms, 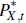, is equal to:

where 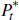is the foreign price level and 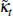governs the relative price between commodities and the basket of goods and services produced overseas. This relative price follows the exogenous process:

where the term in brackets, 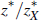, is the steady-state productivity growth differential between the large economy as a whole and the large economy's commodity sector. We include this term for technical reasons to ensure the existence of a well-defined balanced growth path – it plays no role in our analysis. Abstracting from this term, along a balanced growth path relative commodity prices experience transitory shocks according to the process:

where u_κ,t is independently and identically distributed N(0, 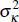). After detrending the variables, κ determines the long-run unconditional mean of commodity prices and the domestic economy's terms of trade.

In estimation, we allow for breaks in κ and 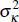, possibly occurring at different dates in the sample. A break in κ implies a change in long-run commodity prices, while a break in σ_κ implies a change in the variance of shocks to commodity prices.

2.3 Trending Relative Prices and Productivity

Our model allows productivity growth in the various sectors of the economy to differ in steady state. These differences in productivity growth translate into steady-state drifts in relative prices. Permanent changes in commodity prices influence other relative prices in the economy. Accounting for existing trends in relative prices helps us to separate changes in relative prices due to changes in long-run commodity prices from pre-existing trends associated with the economy's balanced growth path.

To illustrate the productivity processes and their link to relative prices, consider the production function for firm i in sector j:

where Y_j,t (i) is the output of firm i, K_j,t (i) and L_j,t (i) are the capital and labour inputs employed by firm i and A_t, Z_t and 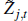are productivity processes.

A_t is a stationary productivity process, common to the non-tradeable, non-commodity tradeable and commodity sectors, that evolves as:

Z_t is a labour-augmenting productivity process, also common to the non-tradeable, non-commodity tradeable and commodity sectors, whose growth rate, z_t = Z_t/Z_t−1, evolves as:

where z determines the steady-state growth rate of aggregate technology in the economy. The processes A_t and Z_t differ because an innovation to A_t has a temporary effect on the level of productivity, while an innovation to Z_t has a permanent effect on the level of productivity.

The final productivity process, 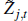, is a stationary sector-specific productivity process that follows:

The parameter z_j determines the differential growth rate, along the balanced growth path, between the output of sector j and real GDP. The stationary process Z_j,t gives rise to temporary departures from the differential trend by:

Along a balanced growth path aggregate variables, including GDP, consumption and the capital stock, grow at the rate of aggregate productivity, z. Sectoral variables, such as the output of non-tradeable goods, Y_N,t, and the quantity of these goods that enter consumption and investment baskets, C_N,t and I_N,t, grow at aggregate productivity growth adjusted by the sector-specific trends. For example, the steady-state growth rate of non-tradeable output is z ×z_N.

Balanced growth requires that the shares of each sector in nominal GDP remain constant. For this to occur, the relative prices of each sector must offset the sector-specific productivity growth rates. For example, the relative price between non-tradeable goods and consumption goods, P_N,t/P_t, must grow at 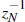along a balanced growth path. In this way, differential trends in productivity growth lead to drifts in relative prices.

In addition to differential productivity growth between the economy's production sectors, we also allow for differential productivity growth between investment and consumption goods as well as between goods produced in the small economy and those produced abroad. As was the case for sectoral productivity growth differentials, these differentials lead to drifts in relative prices along the balanced growth path.