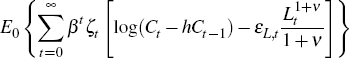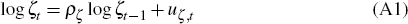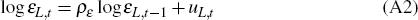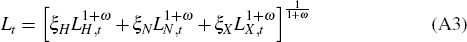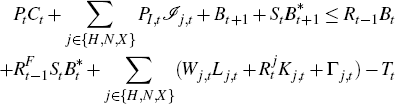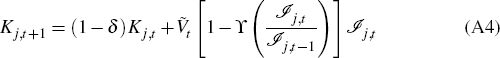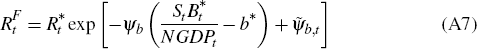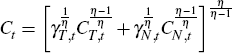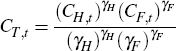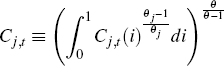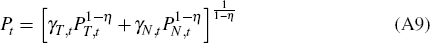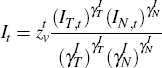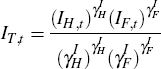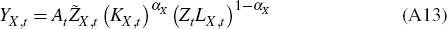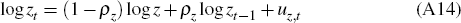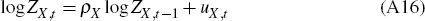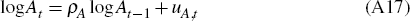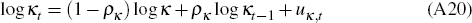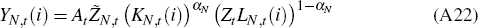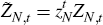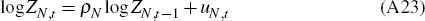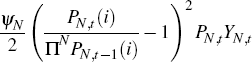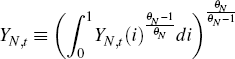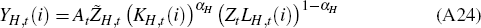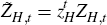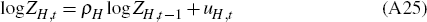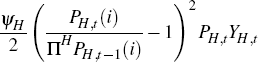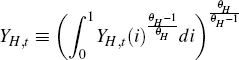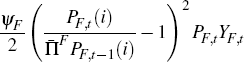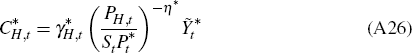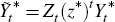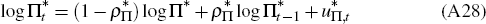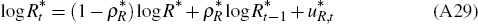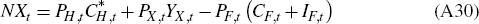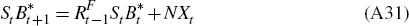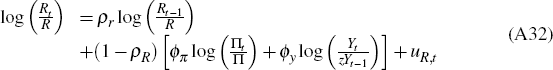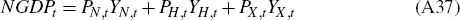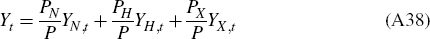RDP 2015-11: Unprecedented Changes in the Terms of Trade Appendix A: Model

In this appendix we describe the basic structure of the model. For a full derivation of the first order conditions and results, please consult the online appendix.

A.1 Households

The preferences of a typical household in the small open economy are given by:

where E₀ denotes the time 0 conditional expectation, β is the household's discount rate, C_t is consumption, L_t is labour supply and h ∈ [0,1] governs the degree of external habit formation. The variable ζ_t is an intertemporal preference shock that follows the stochastic process:

with u_ζ,t independently and identically distributed N(0, 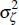). The variable ε_L,t is a labour supply shock that follows the process:

with u_L,t independently and identically distributed N(0,).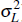

Aggregate labour supply consists of labour supplied to the home-tradeable goods sector, L_H,t, the non-tradeable goods sector, L_N,t, and the commodity-exporting sector, L_X,t, according to the constant elasticity of substitution (CES) bundle:

Workers view employment in different sectors as imperfect substitutes. The parameter ω controls the willingness of workers to move between sectors in response to wage differentials, while the parameters ξ_H, ξ_N and ξ_X govern the relative desirability of supplying labour to each sector.

The household enter the period with K_j,t units of capital from sector j ∈ {H,N,X}, B_t units of one-period risk-free bonds denominated in domestic currency and 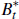units of one-period risk-free bonds denominated in foreign currency. During the period, the household receives wages, returns on capital and profits and pays lump sum transfers to the government. The household uses its income to purchase new bonds, to invest in new capital and to purchase consumption goods. The resulting flow budget constraint is:

where P_t is the consumer price index, P_I,t is the price of the aggregate investment good, 𝓙_j,t is investment in sector j, W_j,t, 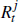and Γ_j,t are the wage rate, the rate of return on capital and profits in sector j, T_t are lump-sum transfers, R_t and 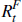are the gross interest rates on risk-free bonds in domestic and foreign currency and S_t is the nominal exchange rate, defined as the domestic price of foreign currency.

The capital stock of each sector evolves according to the law of motion:

for j ∈ {H,N,X} where δ is the capital depreciation rate and ϒ is an investment adjustment cost with the standard restrictions that in steady state ϒ(•) = ϒ′ (•) = 0 and ϒ″ (•) > 0. Ṽ_t governs the efficiency with which investment adds to the capital stock. It follows the process:

where z_I is the differential between the growth rate of real investment and the growth rate of labour-augmenting technology, z. V_t is a stationary autoregressive process that affects the marginal efficiency of investment of the form:

where u_V,t is identically and independently distributed N(0,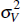). On the balanced growth path ${\mathcal{I}}_{j,t}$ grows at z×z_I. The term on the right hand side of Equation (A4), ${\tilde{V}}_t{\mathcal{I}}_{j,t}$ , grows at z. Thus, the trend in Ṽ_t enables a balanced growth path in which real investment grows faster than real consumption.

As explained by Schmitt-Grohé and Uribe (2003), to ensure stationarity we link the interest rate that domestic residents pay for foreign borrowing to the economy's net foreign asset position. The interest rate on foreign bonds is given by

where 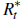is the foreign interest rate, b* is the steady-state net foreign asset-to-GDP ratio and NGDP_t is nominal GDP. 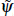_b,t is a risk premium shock that follows the process:

where u_ψ,t is independently and identically distributed N(0, ).

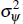A.2 Final Goods-producing Firms

The economy features two final goods: a composite consumption good and a composite investment good. We describe each in turn.

A.2.1 Final consumption goods

Final consumption goods are produced by a representative competitive firm that combines non-tradeable and tradeable consumption goods according to the technology:

where C_N,t is the output of the non-traded sector that is directed towards consumption and has price P_N,t while C_T,t is the output of the traded sector that is directed towards consumption and has price P_T,t. The deterministic processes γ_T,t and γ_N,t ensure, as in Rabanal (2009), that expenditure shares remain stationary along the balanced growth path.^[19] C_T,t is a composite of domestically produced and imported tradeable goods assembled according to the technology:

The Cobb-Douglas specification guarantees that the expenditure shares in the tradeable consumption basket remain constant. This assumption is convenient to find the normalisations to make the system stationary. Otherwise, γ_H and γ_F would have to trend to keep nominal expenditure shares constant in steady state. The trends in γ_H and γ_F, together with the differential growth rate of the home-tradeable producing goods, z_H, and the differential growth rate of the foreign goods producing sector, z*, would determine the differential growth rate of the tradeable basket, that is, z_T. But to find the trends in γ_H and γ_F one must know z_T.

The non-traded, domestically produced traded and imported consumption goods are all bundles of a continuum of imperfectly substitutable goods:^[20]

for j ∈ {H,N,F}. Profit maximisation and the zero-profit condition imply that the price of the final consumption good is a CES aggregate of the prices of the non-tradeable and tradeable consumption goods:

and the price of the tradeable consumption good is a Cobb-Douglas aggregate of the home-produced and imported goods:

A.2.2 Final investment goods

Final investment goods are produced by a representative competitive firm according to the technology:

where I_N,t is the output of the non-traded sector directed towards the production of investment, I_T,t is the output of the traded sector that is directed towards investment and z_v is a productivity trend that, jointly with the growth rates of I_T,t and I_N,t, determines the steady state growth rate of final investment, z_I.^[21] I_T,t is a composite of domestically and foreign-produced tradeable goods that is assembled according to the technology:

The corresponding price indices are:

and

As the shares of non-tradeable, domestically produced tradeable and imported goods in the investment and consumption composites differ, the price of final consumption goods, P_t, will differ from the price of investment goods, P_I,t. Similarly, the price of tradeable consumption goods, P_T,t, will differ from the price of tradeable investment goods, .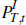

A.3 Intermediate Goods-producing Firms

The economy features four intermediate good producers: commodity firms, non-tradeable firms, domestic non-commodity tradeable firms and importing firms. We describe each in turn.

A.3.1 Commodity-exporting firms

Commodity firms produce a homogeneous good in a perfectly competitive market using the Cobb-Douglas production function:

where Z_t is a labour-augmenting technology shock, common to all producing sectors, whose growth rate, z_t = Z_t/Z_t−1, follows the process:

where z > 1 determines the trend growth rate of real GDP and u_z,t is independently and identically distributed N(0, 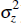). The sector-specific productivity process, 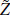_X,t, follows

where z_X > 0 determines the differential growth rate, along the balanced growth path, between the output of the commodity-exporting sector and real GDP. The stationary process Z_X,t gives rise to temporary departures from the differential trend by:

where u_X,t is independently and identically distributed N(0, 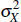). In Equation (A13) A_t is a stationary technology shock, also common to all sectors, that follows the process:

where u_A,t is independently and identically distributed N(0, ).

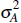Commodity producers take prices as given. These prices are set in world markets and are unaffected by domestic economic developments. Specifically, we assume that the price of commodities, in foreign currency terms, is equal to:

where 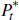is the foreign price level and 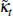, which governs the relative price of commodities, follows the exogenous process:

where z* is the differential growth rate of foreign output and 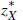is the differential growth rate of foreign production of commodities. The drift in the relative price of commodities reflects the relative productivity growth of the commodity sector and the foreign economy. Along the balanced growth path, relative commodity prices experience transitory shocks according to the process:

where u_κ,t is independently and identically distributed N(0, 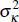). For the stochastically detrended variables, κ determines the unconditional mean of the terms of trade and, in turn, is one of the determinants of the economy's steady state. In estimation, we allow for breaks in κ and in σ_κ, possibly occurring at different dates in the sample.

The law of one price holds for commodities. This means that their price in domestic currency terms is:

A.3.2 Non-tradeable goods-producing firms

Non-tradeable firms sell differentiated products, which they produce using the Cobb-Douglas production function:

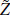_N,t is sector-specific productivity process that follows:

where z_N > 0 and Z_N,t are transitory deviations from the sector-specific trend that follow the process:

where u_N,t is independently and identically distributed N(0, 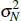). We introduce price stickiness into this sector by assuming that firms can only change prices at some cost, following a Rotemberg (1982) pricing mechanism: ^[22]

where ψ_N governs the size of the price adjustment cost and ∏^N is the steady-state inflation rate of non-tradeable goods prices.

Aggregate non-tradeable output is defined by a CES aggregator:

A.3.3 Domestic non-commodity tradeable goods-producing firms

Domestic tradeable firms produce differentiated products using the Cobb-Douglas production function:

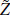_H,t is a stationary sector-specific productivity shock that follows:

where z_H > 0 and Z_H,t are temporary deviations from that trend according to the process:

where u_H,t is independently and identically distributed N(0, 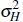). Like their non-tradeable counterparts, tradeable firms can only change prices at some cost, following a Rotemberg (1982) pricing mechanism:

where ψ_H governs the size of the price adjustment cost and ∏^H is the steady-state inflation rate of domestic non-commodity tradeable goods prices. Domestic tradeable output, Y_H,t is an aggregate of the output of each of the domestic tradeable firms:

A.3.4 Importing firms

Importing firms purchase foreign good varieties at the price ζS_t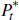 and sell them in the domestic market at price P_F,t(i). The parameter ς represents a subsidy to importing firms, funded by lump-sum taxation. We set the subsidy equal to ς = (θ_F − 1)/θ_F, thereby ensuring that mark-ups in this sector are zero in equilibrium.

Importing firms can also only change prices at some cost, following a Rotemberg (1982) pricing mechansim:

A.4 Foreign Sector, Net Exports and the Current Account

Following Gertler, Gilchrist and Natalucci (2007), we postulate a foreign demand function for domestically produced tradeable goods, 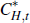, of the form:

Foreign output, 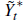, follows the non-stationary process

Transitory deviations from foreign trend growth are captured by 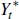which follows:

where 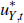is independently and identically distributed N(0, 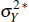). Foreign inflation is assumed to follow:

and the foreign interest rate follows:

where the independently and identically distributed shocks 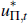and 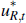are distribute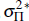d N(0, ) and N(0, ).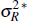

Net exports are given by:

and so the current account equation is given by:

A.5 Monetary Policy

The domestic central bank follows a Taylor rule that responds to deviations of output growth and inflation from their steady-state levels

where ∏_t = P_t/P_t−1 is the inflation rate in terms of final consumption goods prices and ∏ is the central bank's inflation target.

A.6 Market Clearing

Market clearing for investment goods requires that production of these goods equals the quantity demanded by the three domestic production sectors

For the non-tradeable, domestic tradeable and import sectors, market clearing requires that the quantity produced equals the quantity demanded:

Nominal GDP is defined as:

and real GDP is defined as:

Footnotes

See the online appendix for details about the normalisations. [19]

This is also the case for investment, I_j,t for j ∈ {H,N,F}. [20]

Ireland and Schuh (2008) and Justiniano, Primiceri and Tambalotti (2011) are examples of closed economy models with a trend in the price of investment goods and a wedge between the growth rates of real investment and real output. [21]

We assume that these price adjustment costs do not affect the cash flow of firms, but only affect their objective function (see De Paoli, Scott and Weeken (2010) for a discussion of this approach.) Therefore, they do not appear in the resource constraint or net export equations. Assuming instead that these adjustment costs are real costs would yield equivalent results as quadratic terms do not appear in the linearised system. [22]