RDP 2015-11: Unprecedented Changes in the Terms of Trade 4. Empirical Analysis
August 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.15MB
The model's structural parameters can be thought of as belonging to two categories: those that can only determine dynamics – persistence parameters, adjustment cost parameters, policy rule parameters and the standard deviations of the model's structural shocks – and those that, in addition to influencing the dynamics, pin down the steady state. We estimate the first category of parameters and calibrate the second, with the exception of h, the parameter that determines the degree of habit persistence, and Δκ, the change in the long-run level of commodity prices, both of which we estimate.
4.1 Calibration
We calibrate for two reasons. First, not all parameters are well identified given the usual choice of observable variables. Second, estimation could imply a steady state at odds with long-run features of the data. Accordingly, we set the parameters governing the steady state so that the model's balanced growth path is in line with the first moments of the data.
The traditional approach of matching sample means seems inappropriate in our case because we postulate a possible break in the long-run level of the terms of trade, which in turn leads to changes in unconditional means. We instead focus on matching features of the data over the first part of the sample, before commodity prices started to rise rapidly. To be precise, although our estimation sample spans 1993:Q1 to 2013:Q4, we calibrate the model's parameters to match moments of the data over the period 1993 to 2002, which was a time of relative stability in the terms of trade (Table 1). In the initial steady state, we first set the long-run level of relative commodity prices, κ, to 1. Before other parameters are calibrated, this choice is a normalisation. After that, of course, a change in κ alters the steady state. For the data to be consistent with the model in estimation we normalise the index of real commodity prices so that it averages 1 over the sub-sample.
Our calibration strategy is as follows. We calibrate the model at a quarterly frequency. We assume that the steady-state rate of labour augmenting productivity growth, z, is 1.0049, which matches the average growth rate of per capita GDP over our sample.[7] We set the central bank's inflation target, ∏, to an annual rate of 2.5 per cent. This is the middle of the Reserve Bank of Australia's inflation target and roughly equal to the mean of inflation over our sample. We set the household's discount rate, β, equal to 0.99625. Together, these three parameters imply a steady state nominal interest rate of 6 per cent.
We set the foreign productivity growth differential, z*, to match the average growth rate of Australia's major trading partners. We set the sector-specific productivity growth differentials, zH and zN, so that the inflation rates of tradeable and non-tradeable goods match their rates in the data. This means that, in steady state, non-tradeable prices increase faster than consumer prices, while tradeable prices increase more slowly.
| Parameter | Description | Value |
|---|---|---|
| β | Household discount rate | 0.9963 |
| δ | Capital depreciation rate | 0.005 |
| ν | Labour supply parameter | 2 |
| ω | Intersectoral labour supply elasticity | 1 |
| ξN | Constant on non-tradeable labour supply | 100 |
| ξH | Constant on tradeable labour supply | 209 |
| ξX | Constant on commodities labour supply | 4,167 |
| ψb | Risk premium | 0.001 |
| γN | Non-tradeables consumption weight | 0.48 |
| γH | Home-produced tradeables weight | 0.643 |
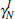 |
Non-tradeables investment weight | 0.664 |
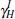 |
Home-produced tradeables investment weight | 0.172 |
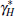 |
Determinant of foreign demand | 0.877 |
| η | Elasticity of substitution in the domestic economy | 0.8 |
| η* | Elasticity of substitution in the foreign economy | 0.8 |
| z | Steady-state productivity growth | 1.0049 |
| zv | Investment growth rate differential | 1.0035 |
| zN | Non-tradeable growth differential | 0.999 |
| zH | Home-tradeable growth differential | 1.002 |
| zX | Commodity growth differential | 1.0 |
| z* | Foreign productivity growth differential | 1.0003 |
| αN | Capital share in non-tradeables | 0.358 |
| αH | Capital share in tradeables | 0.438 |
| αX | Capital share in commodities | 0.70 |
| ∏ | Domestic inflation target | 1.0062 |
| ∏* | Foreign inflation target | 1.0055 |
| θN | Mark-up in non-tradeables | 11 |
| θH | Mark-up in home tradeables | 11 |
| θF | Mark-up in imports | 11 |
| b* | Steady-state net foreign assets-to-GDP ratio | 0 |
We set the capital shares in each sector, αN, αH and αx, according to their average values in national accounts data.[8] The mark-up parameters, θN, θH and θF, are set so that each sector has an an average mark-up of 10 per cent. However, we estimate the price adjustment cost parameters that determine the slope of the Phillips curves for these sectors.
We set the parameter governing the elasticity of labour supply, ν, to 2, which is a standard value in the literature. In line with Horvath (2000), we set the parameter governing the willingness of workers to move between sectors in response to wage differentials, ω, to 1. Given those parameters, we adjust the parameters governing the amount of labour supplied to each sector in steady state, ξN, ξH and ξx, so that the shares of hours worked in each sector approximates those in the data.
We set the parameters governing the share of non-tradeable, non-commodity tradeable and imported goods in the small economy's consumption and investment baskets to match averages in the data and the parameter governing steady-state foreign demand for non-commodity tradeable goods to match the share of exports in GDP.
Table 2 compares the moments implied by the model's steady state to their empirical counterparts. At the calibrated parameters values of Table 1, the model's steady state does quite well. An exception is investment growth, whose mean is somewhat lower in the model than in our sample. Because investment is volatile and can contract significantly in recessions, it is likely that the growth rate of investment in our sample (which does not include a recession) is overstated. If we extend the sample to begin in 1990:Q1 – which includes a recession – the average growth rate of investment is 3.5 per cent. This is close to the model implied growth rate of 3.4 per cent.[9]
| Target | Data | Model | |
|---|---|---|---|
| 1993–2013 | 1993–2002 | ||
| Macro aggregates (annualised, per cent) | |||
| Per capita output growth | 1.96 | 2.64 | 1.96 |
| Per capita investment growth | 4.31 | 4.39 | 3.43 |
| Inflation | 2.63 | 2.50 | 2.50 |
| Tradeable inflation | 1.65 | 2.09 | 2.09 |
| Non-tradeable inflation | 3.41 | 2.86 | 2.86 |
| Investment deflator inflation | 1.29 | 1.09 | 1.09 |
| Expenditure (per cent of GDP) | |||
| Consumption | 74.6 | 75.8 | 72.7 |
| Investment | 26.3 | 24.7 | 27.3 |
| Exports | 19.5 | 19.3 | 19.7 |
| Consumption basket (per cent of consumption) | |||
| Non-tradeable consumption | 55.2 | 53.4 | 53.4 |
| Home tradeable consumption | 27.3 | 30.0 | 30.0 |
| Imported tradeable consumption | 17.5 | 16.6 | 16.6 |
| Investment basket (per cent of investment) | |||
| Non-tradeable investment | 67.4 | 66.4 | 66.4 |
| Home tradeable investment | 2.6 | 5.7 | 5.8 |
| Imported investment | 30.0 | 27.9 | 27.8 |
| Exports (per cent of exports) | |||
| Resource exports | 42.1 | 34.6 | 34.6 |
| Other exports | 57.9 | 65.4 | 65.4 |
| Employment (per cent of hours worked) | |||
| Non-tradeable | 67.6 | 65.0 | 64.3 |
| Home tradeable | 31.1 | 34.0 | 33.2 |
| Commodity | 1.3 | 1.0 | 2.5 |
Note: Model ratios calculated at initial regime with  = 1.0 and h
= 0.5 = 1.0 and h
= 0.5
|
|||
4.2 Estimation
We estimate the model using Bayesian methods, as is common in the estimated DSGE literature.[10] Our case, however, is non-standard because we allow for structural change and jointly estimate two sets of distinct parameters. These are: (i) the structural parameters of the model, ϑ, that have continuous support; and (ii) the dates of structural changes, T = (Tκ, Tσκ) that have discrete support (Tκ is the date break in the mean and Tσκ is the date break in the variance of commodity prices).
The joint posterior density of ϑ and T is:
where 𝓨 ≡ 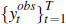 is the data and
is the data and 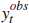 is a nobs x 1 vector of observable variables.
is a nobs x 1 vector of observable variables.
The likelihood is given by 𝓛(𝓨|ϑ,T) and p(ϑ,T) is the prior probability of observing the parameters ϑ and T. Kulish and Pagan (2012) discuss how to construct 𝓛(𝓨|ϑ, T) in models with forward-looking expectations and structural changes. The priors for the structural parameters and the date breaks are taken to be independent, so that p(ϑ,T) =p(ϑ)p(T). We use a flat prior for T so p(T) ∝ 1, which is proper given its discrete support. We set a trimming parameter to prevent breaks in the long-run mean of commodity prices from occurring with the first or last four years of our sample. Our online appendix describes the posterior sampler.
We estimate the model using quarterly Australian macroeconomic data for the period 1993:Q1 to 2013:Q4. The starting date coincides with a period around the beginning of inflation targeting in Australia, providing us with a sample in which the macroeconomic policy environment has been broadly stable.
Our data series includes aggregate and sectoral Australian variables and foreign variables. The aggregate data include GDP, investment, consumption, net exports, hours worked, the cash rate, trimmed mean inflation and the percentage change in the nominal exchange rate. The national accounts variables and hours worked are all expressed in per capita terms and seasonally adjusted. Output, investment, consumption and hours all enter as percentage changes, while net exports enter as a share of nominal GDP. We also include two sectoral variables in the model: the inflation rate of non-tradeable goods and the ratio of nominal non-tradeable consumption to aggregate nominal consumption. The foreign variables that we include in the model are output growth, interest rates and inflation. We take the growth rate of Australia's major trading partners’ GDP constructed by the Reserve Bank of Australia as the measure of foreign output growth. For interest rates we use the average of the policy rates in the United States, the euro area and Japan.[11]
For the foreign inflation rate, we use the trade-weighted average inflation rate of Australia's major trading partners. The 14 series we use in estimation are shown in Figure 3. Appendix B contains a complete description of the data sources, calculations and transformations.
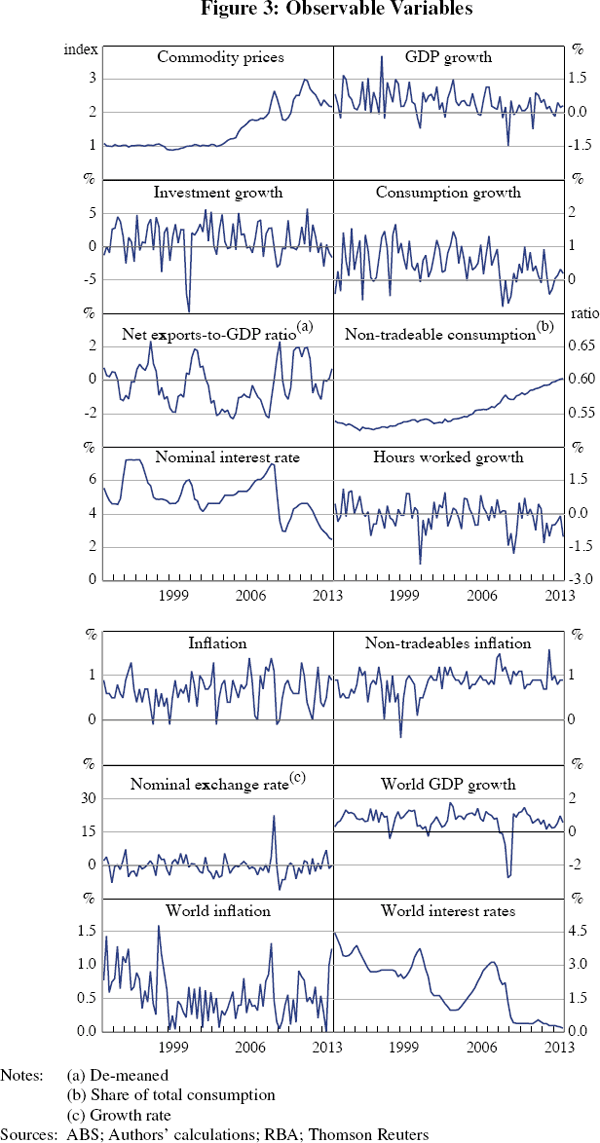
Macroeconomic data are measured with noise and economic concepts in the model do not always match the measures in the data. To account for this, we add measurement error in estimation.
4.3 Priors
We choose a uniform prior with support −0.25 to 3.5 for Δκ, which is the parameter of most interest in our analysis.
This means that the estimation is free to choose a steady state in which the
long-run level of commodity prices declined by 25 per cent, increased by 350
per cent or took any value in between. We set the same inverse gamma priors
for the standard deviation of shocks to commodity prices in the initial volatility
regime, σκ, as we do for the standard deviation
of shocks to commodity prices in the later volatility regime, 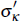 . That is, we do not
take a stand on whether commodity price shocks have become more or less volatile
over our sample.
. That is, we do not
take a stand on whether commodity price shocks have become more or less volatile
over our sample.
Our other choices are in line with the literature. We impose loose beta distributions on the autoregressive parameters and inverse gamma distributions on the standard deviations of the shocks. For the parameters of the monetary policy rule we set a prior mean of 1.5 for the response of the nominal interest rate to inflation and of 0.3 for the response to real output growth.
Footnotes
We calibrate this parameter using the average growth over our full sample of data rather than the shorter 1993 to 2002 sample because the shorter sample featured an unusually rapid period of economic growth in Australia associated with a steep recovery from a deep recession in the early 1990s and a period of rapid productivity growth due, in part, to a series of microeconomic reforms in the 1980s. Consequently, the full-sample average is likely to better reflect the long-run productivity growth rate. [7]
Appendix B provides additional detail regarding our classification of industries into tradeable, non-tradeable and commodity-exporting. [8]
We did not calibrate the model to match this parameter specifically. Instead, we set zv, which governs the growth rate of investment, so as to match the rate of inflation of investment goods prices. [9]
See An and Schorfheide (2007) for a description of these techniques. [10]
Prior to the introduction of the euro, we construct this series using the German policy rate. [11]