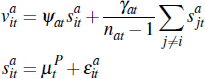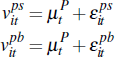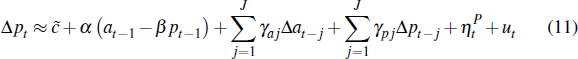RDP 2014-09: Predicting Dwelling Prices with Consideration of the Sales Mechanism 5. Why Does the Mechanism of Sale Matter?
September 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 822KB
This section shows how the micro structure of the different trade mechanisms, and the nature of shocks to agents' valuations, can provide an interpretation of our previous empirical findings. The first step is to justify our assertion that, relative to private-treaty prices, prices at auctions are more responsive to shocks to buyers' valuations than they are to sellers' valuations (Section 5.1). The second step is to rationalise why buyers' valuations respond to new information about dwelling prices more quickly than sellers' valuations (Section 5.2). The third is to bring these two results together to explain our previous empirical findings (Section 5.3).
5.1 Some Intuition for the Theory
We begin by considering the simplest trade mechanisms: an ascending open-bid (or English) auction (the mechanism most commonly used in Australia), without a seller reserve price, to model auctions; and a Nash bargaining solution to model sales that use bilateral private-treaty negotiations. In the English auction, the price rises until no bidder (hereafter buyer) is willing to offer more. In the Nash bargaining solution, the price is a weighted average of the buyer and seller valuation. To further simplify, we assume that buyers at auctions have private values,[18] and that any buyer values the dwelling more than any seller. That is, the dwelling is always sold through either mechanism. These assumptions are unrealistic, but they are useful to provide the basic intuition. They are relaxed in a formal analysis below.
It is a dominant strategy for a buyer to bid until the point at which his or her private valuation is reached, and then exit the auction.[19] Thus, bidding continues until the buyer with the second-highest valuation exits the auction, leaving only the buyer with the highest valuation who wins the auction and pays a price equal to the second-highest valuation. An implication of this model is that a common shock to all buyers' valuations will increase the auction price one for one. Furthermore, since there is no seller reserve, sellers' valuations have no effect on the equilibrium auction price.
In a private-treaty negotiation with Nash bargaining, a shock to the buyer's valuation will only partially increase the price, since the negotiated price is a weighted average of the buyer's and seller's valuation. In particular, the price will only go up by the weight on the buyer's valuation, which under Nash bargaining, reflects the relative bargaining strength of the seller.[20] In a market where buyers and sellers have equal bargaining power, prices will be equally responsive to a common shock to buyers' valuations as they are to a common shock to sellers' valuations. Only if sellers have all the bargaining power will private-treaty prices behave like auction prices, responding only to buyer shocks and not seller shocks.
The assumptions we have maintained so far, that all auctions and bilateral negotiations end in a sale and that buyers have private values, are useful in making our general point, but they are restrictive. We relax them below.
5.1.1 When not all auctions or negotiations end in a sale
When not all auctions end in a sale, sellers' valuations will matter. To incorporate this phenomenon in our theoretical analysis, we consider the reserve price, which is a minimum price demanded by the seller. In auctions in NSW and Victoria, a vendor bid, which is a bid made by the auctioneer on behalf of the seller, can be used to effect a reserve price that conditions on the information revealed through the auction.[21] Alternatively, the seller can simply choose not to sell the property if bidding does not exceed their reserve price.[22]
The first implication of the seller using a reserve price R is that not all auctions end in a transaction: when R is above the valuation of the highest buyer the dwelling does not sell. R can affect the value of the winning bid: when R is below the valuation of the highest buyer, but higher than the second-highest buyer's valuation, the dwelling sells at the price R. Only when R is below the second-highest buyer's valuation does the reserve price have no effect on the auction outcome or the price obtained.
Consider now the effect on the auction price of an increase in R. When the auction ends without a sale, an increase in R has no effect on the auction outcome or the absence of price due to the fact the dwelling is passed in. When the auction is successful, there are three possible cases: one, an increase in R does not cross the threshold of the second-highest buyer's valuation and so has no effect on the equilibrium price; two, it does cross the threshold, in which case an increase in R will affect prices but less than one for one (by the amount by which R exceeds the second-highest valuation); and three, R is initially above the second-highest valuation and is raised, increasing prices one for one. If R becomes too high, however, crossing the valuation threshold for the buyer with the highest valuation, the auction is passed in and excluded from the dwelling price transactions data.
Thus R plays one of two roles, if any, at a given auction: either an increase in R weakly increases the winning bid to the seller, with the magnitude depending upon the initial and final values of R in relation to the highest and second-highest buyer valuations; or it prevents a trade that would otherwise occur from taking place. The latter is a selection effect and leads to higher prices in the observed transactions data. The total effect of a change in R on the average auction price is the weighted average of these two effects.
Our interest is in how shocks to sellers' valuations affect the average auction price in this more complicated environment. The effect operates solely through the reserve price. Thus, the effect of a common shock to sellers' valuations is the composition of the effect of the shock on reserve prices and the effect of the reserve price on the transaction price. Assuming that the seller chooses the reserve price optimally – that is, with the goal of maximising the expected auction price – we can determine the overall effect conditioning on the distribution of buyers' valuations and that of sellers. When both are uniform, and there are more than three buyers, then the effect of a seller shock on average price is an order of magnitude less than that of a buyer shock. This conclusion holds more generally among (weakly) left-skewed distributions that belong to the generalized Pareto distribution family, and which nests the uniform distribution.
The arguments for private-treaties with Nash bargaining are quite different. In private-treaties, an increase in all sellers' valuations will increase prices in transactions that remain profitable to the buyer and the seller by the amount of the buyer's bargaining weight. This also results in a selection effect, removing from the transactions data those dwellings where the seller now values the dwelling more than the buyer they meet. What we show below is that if the dispersion of buyers' and sellers' valuations are constant, then the selection effect is again less important for changes in private-treaty prices. What is of primary importance is the sensitivity of prices to average buyers' and sellers' valuations, as reflected in the relative bargaining strengths of the two groups. Unless there is a special reason to believe that sellers have all of the power in dwelling transaction negotiations, in all states of the dwelling price cycle, it is difficult to move away from the interpretation that both buyers and sellers are important in changes in private-treaty prices.
5.2 Differences in the Response to New Information
The previous intuition argues that changes in auction prices mainly reflect changes in buyers' valuations, whereas changes in private-treaty prices reflect changes in both buyers' and sellers' valuations. If we extend this argument, and assume that buyers' valuations respond more quickly to news relevant to dwelling prices than do sellers', these two facts can explain the previous empirical findings: that auction price growth is not highly autocorrelated but private-treaty price growth is; that auctions are more useful for forecasting; and that auctions better reflect the common trend in all prices.
In particular, if there is a shock to the common stochastic trend in all prices (which is a permanent shock), and all buyers update their valuations quickly, then auction prices must be indicative of the common trend and respond quite quickly to permanent shocks as highlighted in Figure 3. Conversely, if sellers update their valuations more slowly, private-treaty prices will still be indicative of the common trend (prices are cointegrated), but will also measure transitory departures from this trend. This can explain why private-treaty price growth is more autocorrelated than auction price growth (because the transitory component induces autocorrelation); why auction prices are more useful for forecasting (because they quickly capture changes in the common trend, whereas it takes more time for private-treaty prices to fully update to this trend); and why auction prices are a better measure of the underlying common stochastic trend – because they are not perturbed by transitory shocks that are specific to sellers' valuations.
Theoretical explanations for why sellers respond more slowly include: equity lock-in (Stein 1995; Genesove and Mayer 1997); rigidity of seller reservation prices due to reference point pricing, whether with respect to the seller's purchase price (Genesove and Mayer 2001) or original list price; and differential non-centralised information flows (Carrillo 2012; Genesove and Han 2012). We now consider the more formal analysis that underpins the previous intuition.
5.3 A More Formal Treatment
We consider two simple models of price determination; an affiliated values English auction and a Nash bargain for bilateral (private-treaty) negotiations. These two models are plausible characterisations of the Australian property market. A formal description of the two models is outlined in Appendix B.
5.3.1 Auction prices
Focusing first on auctions, we assume that in each quarter there are many English auctions – the auction mechanism most commonly used in the Australian housing market. In any one auction, bids are observed by all other buyers and the buyer with the highest bid wins, paying that amount. We assume that buyers are risk neutral and have valuations that are linear and affiliated (Milgrom and Weber 1982; Klemperer 1999) as follows:[23]
The valuation of buyer i in auction a held at time t is given by 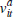 and
and 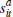 is buyer i's
signal (or estimate) of the value of the dwelling. Importantly, the above modelling
device assumes that buyer valuations are a function of their own signal and
other buyer's signals (in the same auction). As bids are announced during
an auction, buyers update their valuations to reflect the information contained
in other buyers' bids.
is buyer i's
signal (or estimate) of the value of the dwelling. Importantly, the above modelling
device assumes that buyer valuations are a function of their own signal and
other buyer's signals (in the same auction). As bids are announced during
an auction, buyers update their valuations to reflect the information contained
in other buyers' bids.
For example, if there are many buyers who participate in auction a at time t and continue to make bids as the price in that auction rises, then this provides information to other active buyers – namely that many other buyers must have high estimates of that dwelling's value. Each buyer then infers that it is more likely that the true value of dwelling a at time t is high, and revises their own valuation upwards.
What stops the process is that buyers only update their signal partially in response
to the information contained in others' bids (by the weighting 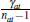 ).
When the price becomes sufficiently high, buyers start to exit the auction
(stop making bids), which is observed by other participants. This continues
until there is a single buyer remaining, at which point the auction concludes
and the dwelling is
sold.[24]
Although we have abstracted from the effects of a seller reserve price, the
underlying intuition remains
similar.[25]
).
When the price becomes sufficiently high, buyers start to exit the auction
(stop making bids), which is observed by other participants. This continues
until there is a single buyer remaining, at which point the auction concludes
and the dwelling is
sold.[24]
Although we have abstracted from the effects of a seller reserve price, the
underlying intuition remains
similar.[25]
We assume that each signal comprises a common component 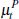 (the common stochastic trend) and an idiosyncratic component
(the common stochastic trend) and an idiosyncratic component 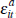 , where the
latter is drawn from a uniform distribution on the bounded interval [−θat, θat].
The weights ψat and γat can
be interpreted as the weights attached to a buyers' own signal and the
mean signal of other buyers in the auction respectively.
, where the
latter is drawn from a uniform distribution on the bounded interval [−θat, θat].
The weights ψat and γat can
be interpreted as the weights attached to a buyers' own signal and the
mean signal of other buyers in the auction respectively.
The assumption of linear affiliation,[26] in conjunction with symmetric bidding strategies and an English auction, implies that the sale price for a successful auction will, in general, be a function of all buyers' signals. For this reason, information is both revealed and aggregated into the price during the auction. It should be noted that the type of affiliation we have modelled can be used to represent, under appropriate restrictions on ψat and γat, either a pure private values auction where valuations are independent, or a pure common values auction where all buyers receive a noisy signal of the same common component in price.
An example of affiliated values is where each buyer has an imperfect signal of the common component of the value of the dwelling and, consistent with the above specification, uses the behaviour of other buyers during the auction to infer it. As buyers are engaged in a search process, the willingness to pay for a dwelling will equal the difference between the net present value of the flow of utility from living in that dwelling, less the value of continued search. Accordingly, there are common factors that will affect all buyers' valuations. Some, like the interest rate, credit terms and other economy-wide factors are likely to be near-perfectly observed; but others, like the quality of a specific dwelling, the prices of similar homes, and the degree of competition from other buyers, are likely to observed with noise, thus leading to the inference problem.
The average auction price is defined as the average price for all successful auctions. Given our assumptions, we show that that this average price can be approximated by (Appendix B.1):
where at is the average auction price and ψt
is the average weight placed on buyers' own signals (averaged across all
buyers in all auctions: 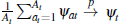 ), and θt is a measure
of the average dispersion of all buyers (again averaged across all buyers in
all auctions:
), and θt is a measure
of the average dispersion of all buyers (again averaged across all buyers in
all auctions: 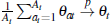 ).
).
The parameter that affects the cointegration relationship with private-treaty prices
is given by βt = ψt + γt.
It reflects the average weight on buyers' own signals and the average weight
on the mean of all other buyers' signals, 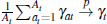 . If βt
is normalised to one, these average weights can be interpreted as information
shares. For example, ψt = 0.7 and γt
= 0.3 would imply that buyers, on average, have 70 per cent of their valuation
formed from their own signal and 30 per cent from the signals inferred from
others' bids during an auction.
. If βt
is normalised to one, these average weights can be interpreted as information
shares. For example, ψt = 0.7 and γt
= 0.3 would imply that buyers, on average, have 70 per cent of their valuation
formed from their own signal and 30 per cent from the signals inferred from
others' bids during an auction.
Importantly, auction prices reflect the common component buyers share in their valuations.
With affiliated values, many buyers and many auctions, auction prices converge
to a linear function of the common price trend, 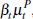 ,
up to a shift factor of ψtθt
. The latter term comprises the average weight that buyers assign to their
own signal, and the average dispersion of buyers' valuations. Thus, for
auctions, an increase in the weight that buyers assign to their own signal
or an increase in the dispersion of buyers' valuations could, in principle,
lead to temporary deviations of auction prices from the common price trend.
,
up to a shift factor of ψtθt
. The latter term comprises the average weight that buyers assign to their
own signal, and the average dispersion of buyers' valuations. Thus, for
auctions, an increase in the weight that buyers assign to their own signal
or an increase in the dispersion of buyers' valuations could, in principle,
lead to temporary deviations of auction prices from the common price trend.
Greater dispersion in buyers' valuations will tend to raise the average price because it is the indifference condition for the second-last buyer remaining (i.e. the point at which the buyer with the second-highest valuation drops out) that is important for determining the final price. With a large number of buyers, greater dispersion in buyers' valuations will not affect the inferred common component of signals from buyers who have already exited the auction, but it will raise the probability that the buyers with the highest and second-highest valuations will have high valuations and so a higher price will be more likely. Accordingly, a higher average auction price could reflect an increase in average buyer dispersion, rather than an increase in the common trend in prices.
Similarly, an increase in the weight that buyers assign to their own signal could also drive a temporary increase in auction prices. Again, this relates to the fact that prices are determined by the indifference condition for the buyer with the second-highest valuation. This buyer, like all buyers, weights their own signal differently to the weight placed on other buyers' signals.[27] In particular, when there are many buyers, the importance of any one buyer (including the buyer with the highest signal) on the mean signal is equal and small. In contrast, the weight the buyer with the second-highest valuation places on their own signal is more important: changes in this weight can lead to transitory changes in auction prices, even when averaged across a large number of transactions.
To understand these results in the context of the intuition given in Section 5.1, we have shown that under more general assumptions about buyers' information, and when there are many buyers in each auction, the argument for the claim that auctions are relatively more responsive to buyers' than sellers' valuations, when compared with private-treaty sales, is similar to the private values case. Including optimal seller reserve prices, set by the seller after he or she has observed the winning bid and therefore on the basis of the information revealed during the auction (Lopomo 2001), introduces a role for the seller's valuation. However, here too, as in the private values case, the responsiveness of average auction prices to a common shock in sellers' valuations is substantially less than to a common shock in buyer valuations. This is true given a sufficient number of buyers and in the baseline uniform distributions case, and with more general left-skewed distributions of buyers' valuations.
5.3.2 Private-treaty prices
For private-treaty prices, we assume that the price is the result of a Nash bargain between one buyer and one seller. That is, the surplus from trade (the difference between the buyer's and the seller's reservation values) is split between the buyer and seller according to their relative bargaining power. Again, we assume that buyers and sellers have a common stochastic trend and an idiosyncratic component in their valuations:
where the prospective seller's idiosyncratic signal, 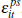 ,
is drawn randomly from a uniform distribution on [−φit,φit]
and the prospective buyer's idiosyncratic signal,
,
is drawn randomly from a uniform distribution on [−φit,φit]
and the prospective buyer's idiosyncratic signal, 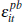 , is drawn randomly
from a uniform distribution on [−θit, θit].
For a sale to occur, the idiosyncratic signal for the buyer must be weakly
higher than that for the seller,
, is drawn randomly
from a uniform distribution on [−θit, θit].
For a sale to occur, the idiosyncratic signal for the buyer must be weakly
higher than that for the seller, 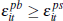 . The average measured private-treaty price
is the average price of all successful private-treaty sales within a quarter.
It can be approximated by (see Appendix B.2):
. The average measured private-treaty price
is the average price of all successful private-treaty sales within a quarter.
It can be approximated by (see Appendix B.2):
The transitory or idiosyncratic components of buyers' and sellers' valuations
are given by the function f, which has the Nash bargaining weight (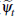 ), the dispersion
of sellers (φt) and the dispersion of buyers (θt)
in its arguments. We assume that the function
), the dispersion
of sellers (φt) and the dispersion of buyers (θt)
in its arguments. We assume that the function 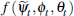 can be approximated
by a stationary autoregressive moving average (ARMA) process to be consistent
with the autocorrelation in private-treaty price growth observed in the data
(Section 3.1).
can be approximated
by a stationary autoregressive moving average (ARMA) process to be consistent
with the autocorrelation in private-treaty price growth observed in the data
(Section 3.1).
The reason that the function f is not zero, even when averaging across a large set of transactions, is that prices only reflect successful negotiations. This implies that buyer and seller valuations are correlated (with all buyer valuations weakly higher than that of the respective seller) and so idiosyncratic factors do not wash out on average.
The valuation of the common component of prices is identical for buyers and sellers
and is assumed not to be predictable: 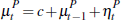 .
We also make the additional assumption that the average overall weight on information
in auctions is constant, βt = β. Under
these assumptions, we can see that average auction prices, Equation (8), and
average private-treaty prices, Equation (9), are cointegrated with cointegrating
vector [1−β]. To link these equations to our empirical
findings, Appendix C shows that Equations (8)
and (9) can be approximated using the VECM:
.
We also make the additional assumption that the average overall weight on information
in auctions is constant, βt = β. Under
these assumptions, we can see that average auction prices, Equation (8), and
average private-treaty prices, Equation (9), are cointegrated with cointegrating
vector [1−β]. To link these equations to our empirical
findings, Appendix C shows that Equations (8)
and (9) can be approximated using the VECM:
This representation is valid provided we assume that average dispersion in buyers' valuations and the average weight that buyers place on their own information (averaged across all auctions in a given quarter) are constant. These assumptions are sufficient for ensuring that changes in auction prices reflect changes in the common price trend, as found in our empirical analysis.
Importantly, the above VECM is fully consistent with our previous empirical findings. In particular, it implies that: growth in auction prices is not autocorrelated; that growth in private-treaty prices is autocorrelated; and that auction prices will Granger cause private-treaty prices but that private-treaty prices will not Granger cause auction prices.
There are four key implications to be drawn from the theoretical analysis. First,
both auction prices and private-treaty prices measure the common trend in all
prices, 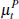 ,
when averaging across a large set of transactions. For this reason, auctions
are not necessarily more efficient at measuring the common trend in all prices.
,
when averaging across a large set of transactions. For this reason, auctions
are not necessarily more efficient at measuring the common trend in all prices.
Second, the different weighting of buyers' and sellers' valuations in different sales mechanisms appears to be important. Assuming our theoretical structure provides a reasonable approximation of actual price formation, our results imply that there is a large set of distributions for which auction prices weight buyers' valuations more highly than sellers' valuations, when compared with private-treaty prices. If this is right, then it follows that the autocorrelation observed in private-treaty prices is more likely to be coming from the valuations of sellers.
Third, since private negotiation is intrinsic in the determination of private-treaty prices, the average dispersion of seller values and the relative bargaining strength of buyers and sellers affect average private-treaty prices. These become plausible sources of autocorrelation in private-treaty prices, but not auction prices.
Fourth, our theory is consistent with the idea that auction prices and private-treaty prices are cointegrated and measure the same common trend. As such, variation in either the average dispersion of sellers or relative bargaining strength can only induce transitory variation in private-treaty prices and must, therefore, dissipate with time.
Footnotes
That is, knowledge of other buyers' valuations has no impact on any given buyer's valuation. [18]
To see why, suppose a seller exited before the price reached their valuation. In this case, there is a positive probability that the buyer could have remained in the auction and paid a price less than their valuation. The buyer has thus forgone a profitable trading opportunity and so this cannot be an equilibrium strategy. Conversely, suppose the buyer remained in the auction when the price is above their valuation. In this case, there is a positive probability the buyer wins and pays a price that is higher than their valuation, thus engaging in trade that is not profitable to them. This also cannot be an equilibrium strategy. [19]
Recall that with a Nash bargain, a stronger seller position implies a transaction price that is closer to the buyer's valuation (and so more of the surplus from trade accrues to the seller). [20]
This is different from a reserve price set prior to the auction. Even if a reserve price is set prior to auction, the ability to make a vendor bid implies that the seller can effectively revise their reserve price, conditioning on information revealed through the auction. In the private values case, the optimal pre-announced reserve price and vendor bid are equivalent. Vendor bids are permissible in both Sydney and Melbourne – see, for example, Consumer Affairs Victoria (2014) and NSW Fair Trading (2014). [21]
Again, refer to Consumer Affairs Victoria (2014) and NSW Fair Trading (2014). [22]
Although the results we derive below are conditioned on the assumption of risk neutrality, this assumption can be relaxed if common values – a specific case of affiliation – are assumed. [23]
Another way to think of our modelling device is that all players in the auction hold a bidding card which remains raised until the price quoted hits the maximum that that buyer is willing to bid, at which point they lower the card and exit the auction, and all other players observe this. Importantly, with affiliation, the maximal bid for any given buyer is a function of both the number of buyers who have already exited the auction and the price point at which each buyer stopped participating. [24]
It also does not materially affect the analysis that follows (see Appendix D). [25]
Intuitively, affiliation of buyers' values implies that there is correlation between values. For example, with two buyers, affiliation implies that an increase in the valuation of buyer 1 also increases the likelihood that buyer 2 holds a higher valuation. The converse is also true: an increase in buyer 2's valuation increases the likelihood that buyer 1 has a higher valuation. Affiliation is a stronger concept than correlation, as it requires local positive correlation everywhere with respect to the joint distribution of valuations (see Klemperer (1999)). [26]
At the price at which the buyer with second-highest valuation is indifferent between
quitting or remaining in the auction, this buyer is comparing their own signal
(with weight ψat) with the likely signal of the other buyer who
has not yet quit (with weight 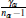 ). The fact that the weight on the second-last
buyer's own signal is potentially different from the weight on the other
buyer's signal (which is the same as for all other buyers who already
exited the auction) means that it is the own-signal weight that becomes pivotal
in price determination. For this reason, a transitory change in the information
weights, towards a greater weight on idiosyncratic information and a lower
weight on other buyers' information, could have a transitory effect on
auction prices.
[27]
). The fact that the weight on the second-last
buyer's own signal is potentially different from the weight on the other
buyer's signal (which is the same as for all other buyers who already
exited the auction) means that it is the own-signal weight that becomes pivotal
in price determination. For this reason, a transitory change in the information
weights, towards a greater weight on idiosyncratic information and a lower
weight on other buyers' information, could have a transitory effect on
auction prices.
[27]