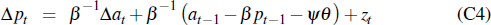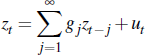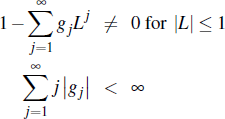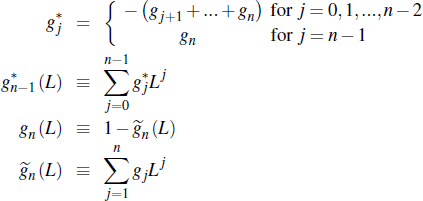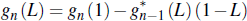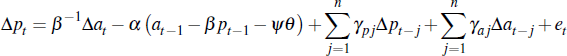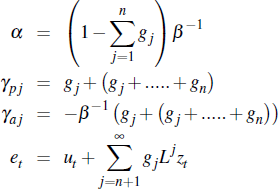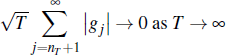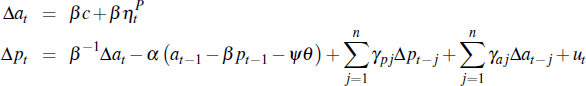RDP 2014-09: Predicting Dwelling Prices with Consideration of the Sales Mechanism Appendix C: Existence of VECM Representation

From the previous sections, auction and private-treaty prices can be approximated by the unobserved components representation:

where we have assumed that total information weight (ψ_t + γ_t = β), the average weight on buyers own information (ψ_t = ψ) and the average dispersion of buyers (θ_t = θ) are all constant. If we further assume that 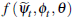can be linearly approximated by a stationary ARMA process, z_t, the above unobserved components model can be written as:

Using a similar approach to the discussion in Lütkepohl (2006, pp 546–548), and noting that z_t and 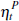are statistically independent of each other, we assume that z_t admits an infinite-order VAR representation:

where u_t is white noise. We further assume the regularity conditions:

Defining:

it is straightforward to verify that:

Pre-multiplying Equation (C4) by g_n (L) and re-arranging terms:

where:

Although we haven't made it explicit, it should be noted that the above coefficients are, in general, functions of the sample size. Taking an asymptotic approximation as the sample size increases, (formally 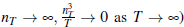given the previous assumptions, implies (see Lütkepohl (2006)):

and so asymptotically the approximation error becomes sufficiently small such that, e_t ≈ u_t .

To recap, we have shown that the unobserved components model in Equations (C1) and (C2) can be approximated by a structural VECM of the form:

Substituting for Δa_t in the second equation yields Equations (10) and (11) in the main text (where we let J = n and 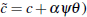.^[29].

Footnote

Although the previous theory is developed for models of prices in levels, it is straightforward to generalise to log-linear models for prices. In the latter, differences in buyers' and sellers' valuations are measured in percentage terms. The log-linear model is strictly equivalent to our empirical regressions. [29]