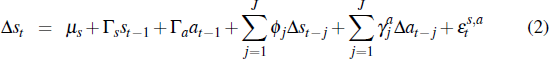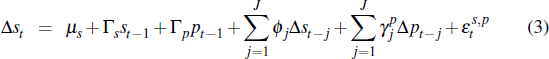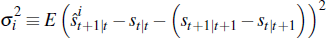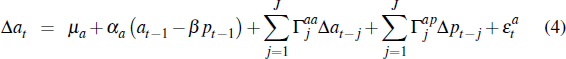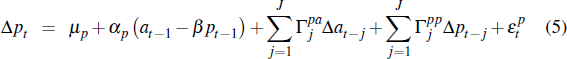RDP 2014-09: Predicting Dwelling Prices with Consideration of the Sales Mechanism 3. Prediction
September 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 822KB
In this section we examine three questions:
- Do auction prices and private-treaty prices have different autocorrelation properties (momentum)?
- Do they perform differently when forecasting out-of-sample?
- Do they perform differently when predicting one another in-sample?
Answering the first question speaks to the well-established literature on the efficiency of housing markets, which suggests that dwelling prices are positively autocorrelated, as discussed in Case and Shiller (1989), Cutler, Poterba and Summers (1991), Cho (1996) and Capozza, Hendershott and Mack (2004) among others. Differences in momentum can also provide insight into the ability of the data to discriminate between alternative theoretical models of the autocorrelation in buyers' and sellers' valuations (this is discussed further in Section 5). The second question addresses whether any gains in predictive content can be useful in real time and considers forecasting growth in a measure of average prices using all sales.
We also consider in-sample analysis, the third question, for three reasons. First, it is possible that revisions to the estimated price indices for either auction or private-treaty prices could affect out-of-sample forecasting performance. By focusing on the full sample of data we are able to abstract from the effects of revisions to the estimated price indices.
Second, in-sample analysis allows us to relax some of the assumptions maintained in the out-of-sample analysis. In particular, using in-sample techniques we can compare the ability of the two series to predict each other without necessarily assuming a vector error correction model (VECM) representation with finite lags.[8] Third, it has been argued that out-of-sample analysis can imply a loss of information and power relative to in-sample analysis (see, for example, Inoue and Kilian (2005)).
3.1 Momentum
Focusing first on the differences in autocorrelation properties, autocorrelation functions show that growth of average prices (all-sales price growth) is positively autocorrelated for up to one year, but that the strongest correlations are for the first two lags of quarterly growth (Figure 2). Considering the autocorrelation functions by sale mechanism highlights that all of the positive autocorrelation in aggregate price growth for Sydney arises from the autocorrelation in private-treaty price growth; there is no evidence to suggest that auction price growth is positively autocorrelated. Indeed, auction prices follow a random walk with drift. This is a quite striking result and suggests that all available information concerning dwelling prices is fully incorporated into auction prices within a quarter, which is consistent with a weak version of the efficient market hypothesis.[9]
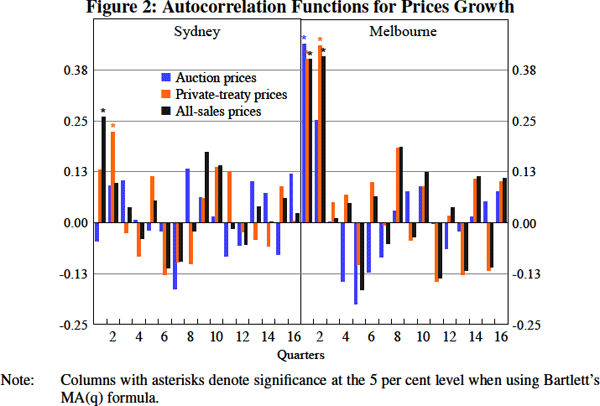
For Melbourne, most of the autocorrelation in all-sales price growth is also driven by autocorrelation in private-treaty price growth, although there is some evidence of first-order autocorrelation in auction price growth. The difference in autocorrelation functions, with private-treaty price growth being more autocorrelated than auction price growth, will subsequently be useful for determining whether buyer or seller valuations are autocorrelated, as discussed further in Section 5.
3.2 Out-of-sample
We now consider whether measures of average prices, separated according to the type of sale, are useful for predicting all-sales price growth out-of-sample and in real time. Specifically, we consider whether the inclusion of either lagged auction prices or lagged private-treaty prices can improve upon the one-quarter-ahead forecasts of all-sales price growth when using a single equation autoregressive model. To do this, we compare the following three forecasting models:[10]
where st is the average dwelling price based on all sales, at is the average auction price and pt is the average private-treaty price (all measured in logs). Equation (1) is the benchmark model, a univariate autoregression in average all-sales price growth. Equation (2) nests the same autoregression, but also includes lags in auction prices. It also allows for all-sales and auction prices to be cointegrated, consistent with the idea that these price measures share the same common trend. Equation (3) incorporates lags of private-treaty prices instead of lags of auction prices and also allows for cointegration.
We define:
for i = 1,2,3 as the respective mean-squared prediction errors (MSPEs)
for one-quarter-ahead all-sales price growth associated with Equations (1),
(2) and (3) respectively. 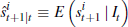 is the one-quarter-ahead forecast of the
log all-sales price level based on Equation i (for i =
1,2,3) and using all available information up to time t. St|τ
is the measured value of the log all-sales price level at time t given
all available information up to time τ≥t. We consider whether
the MSPEs are statistically different between Equations (1), (2) and (3) using
pairwise comparisons and the MSE-t test statistic discussed in McCracken
(2007).[11]
is the one-quarter-ahead forecast of the
log all-sales price level based on Equation i (for i =
1,2,3) and using all available information up to time t. St|τ
is the measured value of the log all-sales price level at time t given
all available information up to time τ≥t. We consider whether
the MSPEs are statistically different between Equations (1), (2) and (3) using
pairwise comparisons and the MSE-t test statistic discussed in McCracken
(2007).[11]
The results in Table 2 suggest that Equation (2) can outperform the benchmark model – that is, there is information content in lagged auction prices. In both cities, the MSPEs for Equation (2) are significantly lower relative to the benchmark model in the order of 10 and 18 per cent for Sydney and Melbourne (column one, rows one and three). In contrast, there is no evidence to suggest that private-treaty prices can also improve upon forecasts relative to the benchmark model; the null that the forecast accuracy of Equation (3) is the same as that of the benchmark cannot be rejected at conventional significance levels (column one, rows two and four).
 |
MSE-t statistic | |
|---|---|---|
| Sydney | ||
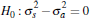 |
0.90** | 0.85 |
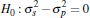 |
0.93 | 0.26 |
| Melbourne | ||
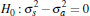 |
0.82** | 1.46 |
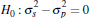 |
0.97 | 0.17 |
Notes: The alternative hypothesis for each test is that the MSPE of the
restricted model, 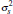 , is greater than the unrestricted alternative
(either , is greater than the unrestricted alternative
(either 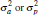 );
recursive estimation is used starting with the sample period from March
1992 to March 2007 for Sydney and from March 1993 to September 2008 for
Melbourne; ***, ** and * denote significance at the 1, 5 and 10 per cent
levels respectively );
recursive estimation is used starting with the sample period from March
1992 to March 2007 for Sydney and from March 1993 to September 2008 for
Melbourne; ***, ** and * denote significance at the 1, 5 and 10 per cent
levels respectively |
||
To further establish whether it is in fact auction prices or private-treaty prices that contain predictive information for future price growth, we consider whether these price measures are useful in predicting one another. Specifically, we use out-of-sample Granger causality tests assuming that auction and private-treaty prices are cointegrated.
The unrestricted model used for our tests is given by:
The null hypotheses are that auction prices do not Granger cause private-treaty prices,
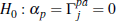 for all j, and that private-treaty prices do not Granger cause auction
prices,
for all j, and that private-treaty prices do not Granger cause auction
prices, 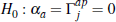 for all j. Testing these hypotheses using the approaches suggested by McCracken
(2007) and Clark and West (2007), the results in Table 3 highlight that we
can reject the null that auction prices do not Granger cause private-treaty
prices, but fail to reject the null that private-treaty prices do not Granger
cause auction prices in Sydney (and only find weak evidence to reject the null
in Melbourne). These results confirm that auction prices appear to be more
useful when forecasting out-of-sample.
for all j. Testing these hypotheses using the approaches suggested by McCracken
(2007) and Clark and West (2007), the results in Table 3 highlight that we
can reject the null that auction prices do not Granger cause private-treaty
prices, but fail to reject the null that private-treaty prices do not Granger
cause auction prices in Sydney (and only find weak evidence to reject the null
in Melbourne). These results confirm that auction prices appear to be more
useful when forecasting out-of-sample.
| Sydney | Melbourne | |
|---|---|---|
| H0 : Auction prices do not Granger cause private-treaty prices | ||
| McCracken: MSE-t | 1.55*** | 1.38** |
| Clark and West: MSPE-adj t | 2.82*** | 2.34*** |
| H0 : Private-treaty prices do not Granger cause auction prices | ||
| McCracken: MSE-t | −1.06 | 0.63* |
| Clark and West: MSPE-adj t | 0.50 | 1.46* |
| Notes: ***, ** and * denote significance at the 1, 5 and 10 per cent levels of significance respectively; McCracken: MSE-t is the Diebold and Mariano test statistic used in the context of a nested model forecast comparison as discussed in McCracken (2007); Clark and West: MSPE-adj t is an alternative test statistic proposed by Clark and West (2007); estimates and out-of-sample forecasts are generated recursively with the initial in-sample estimation period from March 1992 to September 2002 for Sydney, and from March 1993 to September 2002 for Melbourne | ||
3.3 In-sample
Although out-of-sample findings are informative for comparing forecasting performance in real time, a limitation of the previous comparisons is that they can imply a loss of information and power relative to in-sample prediction comparisons (see, for example, Inoue and Kilian (2005)), and can be affected by revisions.
To consider whether these issues are important, we undertake the previous bivariate causality tests in-sample using the testing procedure discussed in Toda and Yamamoto (1995) and Dolado and Lütkepohl (1996). One useful feature of this approach is that it only requires the order of integration of the data to be correctly specified, as the test remains consistent irrespective of whether auction and private-treaty prices are cointegrated or not.[12]
The results in Table 4 highlight that the previous causality results are supported. We are able to reject the null that auction prices do not Granger cause private-treaty prices in both Sydney and Melbourne, but are unable to reject the null that private-treaty prices do not Granger cause auction prices.
| Null hypothesis | Sydney | Melbourne |
|---|---|---|
| Auction prices do not | 68.74*** | 36.70*** |
| Granger cause private-treaty prices | (0.00) | (0.00) |
| Private-treaty prices do not | 5.75 | 2.15 |
| Granger cause auctions prices | (0.30) | (0.71) |
| Notes: All data are treated as I(1) consistent with the results from unit root tests; ***, ** and * denote significance at the 1, 5 and 10 per cent levels respectively; p-values are reported in parentheses | ||
We also conduct two further in-sample specification checks. First, we test the null hypothesis that auction prices follow a random walk with drift, and so cannot be explained using either lagged auction or private-treaty price information.[13] Results from this test for the two cities (available on request), suggest that the null cannot be rejected for Sydney at conventional significance levels; but it can be rejected for Melbourne, as lagged auction prices do appear to contain some predictive content for that city.
In the second, we check whether auction and private-treaty prices share the same common trend in prices and are, therefore, cointegrated as assumed in the previous out-of-sample analysis. Evidence in favour of cointegration, using the full sample of data, is reported in Appendix A. Estimates of the cointegrating vectors and adjustment parameters are reported in Table 5. Consistent with our previous findings, the results highlight that private-treaty prices respond to past deviations between auction and private-treaty prices as the adjustment parameters on the lagged cointegrating relationship – αp in Equation (5) – are significant in both Sydney and Melbourne (column two). In contrast, auction prices do not respond to the same deviation as the adjustment parameters – αa in Equation (4) – are insignificant in both cities (column one). The cointegration parameter, β for each city, also looks reasonable and not too far from 1, as one might expect.[14]
| Auction prices | Private-treaty prices | |
|---|---|---|
| Sydney | ||
| Cointegration parameter | 1 | 1.05*** |
| (.) | (0.01) | |
| Adjustment parameter | −0.10 | 0.42*** |
| (0.23) | (0.15) | |
| Melbourne | ||
| Cointegration parameter | 1 | 1.08*** |
| (.) | (0.01) | |
| Adjustment parameter | −0.02 | 0.18** |
| (0.14) | (0.07) | |
| Notes: Cointegration and adjustment parameter estimates are obtained using Johansen MLE and normalising the coefficient on auction prices to 1; ***, ** and * denote significance at the 1, 5 and 10 per cent levels respectively and are with respect to 0 for the adjustment parameters and 1 for the cointegration parameters; standard errors are reported in parentheses | ||
In sum, the data are consistent with the following empirical facts:
- Forecasts from an autoregression of all-sales prices can be significantly improved upon by including lagged auction price information. Lagged private-treaty prices are less informative.
- Auction prices Granger cause private-treaty prices, but private-treaty prices do not Granger cause auction prices. This holds both in- and out-of-sample.
- The auction price level process is not statistically different from a random walk with drift in Sydney. There is some evidence that the first lag of auction price growth can be used to forecast auction price growth in Melbourne.
- Auction and private-treaty prices are cointegrated.
Footnotes
Although a VECM with finite lags is a natural framework for modelling prices given that they are likely to share the same common trend, it is not an immediate implication of theory and so we build up a case to support this representation, rather than simply assume it is valid (see Appendices B and C). [8]
See, for example, Cho (1996). [9]
In these, and all subsequent out-of-sample forecasting tests, we use four lags when using Sydney data and three lags when using Melbourne data. This is based on likelihood-ratio and residual serial correlation tests, as well as information criteria (see Appendix A). For Melbourne, quarterly seasonal dummies are included as additional control variables, consistent with evidence of seasonality in Melbourne. [10]
The MSE-t statistic we compute is equivalent to the S1 test statistic proposed by Diebold and Mariano (1995). It uses a mean-squared loss criterion, allows for contemporaneous and serially correlated prediction errors, and is computed under the null that the difference in the mean-squared prediction errors (one-quarter-ahead) for two alternative forecasting equations is zero. As noted in McCracken (2007), when working with nested prediction equations the MSE-t test statistic may not be well approximated by a normal distribution, and so we use the alternative critical values tabulated in the same paper. Qualitatively similar results are obtained using the MSPE-adj t statistic suggested in Clark and West (2007). [11]
Conditioning on the assumption of cointegration provides similar results. [12]
This is not a relevant test in the case of private-treaty prices as we have already established that lagged auction prices can be used to forecast them. [13]
Including additional characteristic controls for Melbourne and restricting the sample to begin from December 1997 leads to an estimated β of 1.05. [14]