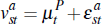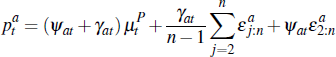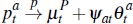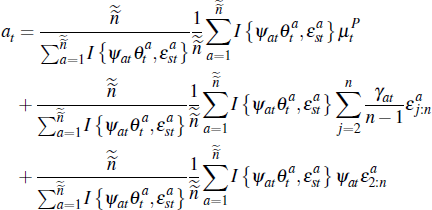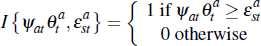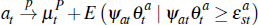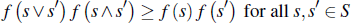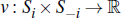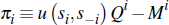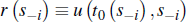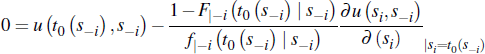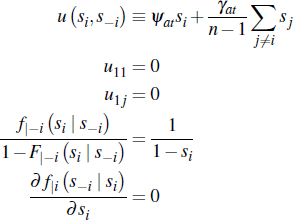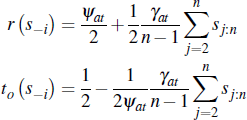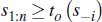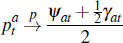RDP 2014-09: Predicting Dwelling Prices with Consideration of the Sales Mechanism Appendix D: Seller Reserve Prices

D.1 Non-optimal Seller Reserve Prices

Consider the case of a non-optimal seller reserve in the English auction. Specifically, there is a single buyer remaining in the auction, and the seller compares the highest outstanding bid with their own (private) reservation value:

where 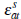is again drawn uniformly on 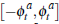. The seller accepts the highest bid made if 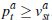, and the sale occurs. If 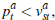the seller rejects the bid and the dwelling is passed in. In the case that the final bid is accepted, the price is given by:

To be clear, seller bids are non-optimal in this case for two reasons. First, as discussed in Milgrom and Weber (1982), sellers choosing a reserve that is not state-contingent and that maximises revenue will, in general, want to disclose the reserve price before the auction commences. Second, as discussed in Lopomo (2001), an optimal seller reserve that conditions on the highest bid (is state-contingent) and that maximises expected revenue, will in general not be the same as the seller's own estimate of the value of the dwelling. We will consider the second case further below. Proceeding under the assumption of a non-optimal reserve price, and assuming for simplicity that ψ_at + γ_at = 1, we note that in an individual auction the price still converges to:

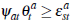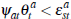as the number of buyers grows large. Whether an individual auction will be successful (with infinitely many buyers) or not will therefore depend on whether , in which case the auction will be successful, or , in which case it will not.

With a non-optimal seller reserve price, the average auction price, is given by:

where we are now explicitly accounting for the fact that there are auctions where the dwelling is passed in, and so 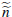is the total number of auctions, including both successful and unsuccessful auctions. 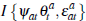is an indicator function such that:

Taking the limit as both the total number of buyers and total number of auctions become large, one can verify that:

and so, in principle, the average auction price depends on the distribution of the upper bound of buyer valuations, the distribution of seller valuations (which is assumed to be independent of the former), and the distribution of weights that buyers place on their own signals.

Nevertheless, as discussed in the main text, for a valid VECM approximation to exist, the selection effect term, 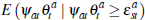, must be approximately constant. If this were not the case, then a VECM with finite lags and serially uncorrelated residuals could not be used to represent the underlying data-generating process. From this perspective, including a non-optimal seller reserve value does not change the main results discussed in the paper. For example, consider the case in which 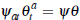and is constant across all auctions. In this case, 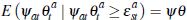but 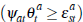is not constant. This is an example of how there can be time variation in the auction clearance rate that is autocorrelated and due to the role of sellers. However, auction prices themselves are not influenced by sellers values nor are they autocorrelated.

D.2 Optimal Seller Reserve Prices

The previous case considered a non-optimal seller reserve price. An alternative case of interest is when sellers set their reserve price optimally. Lopomo (2001, Proposition 1) derives the optimal state-contingent seller reserve price for a seller who maximises their expected revenue when selling an object through an English auction, and where buyer values are affiliated as defined by Milgrom and Weber (1982). We use the word state-contingent here to capture the idea that the seller observes the auction process, and then determines an optimal seller reserve price that can be affected through a single seller (vendor) bid made at the point in which there is only one buyer remaining in the auction. The remaining buyer can then choose to match that bid and the dwelling is sold, or exit the auction and the dwelling is passed in.

Following Lopomo, let the seller face n risk-neutral buyers who participate in an English auction. Define N ≡ {1, …,n}. Each buyer, i ∈ N, observes a private signal of the value of the dwelling, 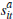, drawn jointly with the other n − 1 signals 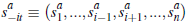from a symmetric distribution with density f that is strictly positive on its support S ≡ [0, 1]ⁿ. The restriction on the support is less general than assumed in the previous appendices, but can matched by assuming that 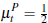and that 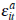is continuously distributed on the support [−½,½]. To conserve notation, we will drop the a superscript and the t subscript, but it should be noted that the following arguments apply to a single auction of dwelling a at time t.

Signals are assumed to be affiliated:

And buyers have a valuation function:

where S_i ≡ [0,1] and S_−i ≡ [0,1]ⁿ⁻¹ and the valuation function v is strictly increasing in its first argument, and weakly increasing and symmetric in its last n−1 arguments such that u (s_i, s_−i ≡ u_i(s₁,…,s_n) for each i ∈ N. The overall pay-off function of buyer i is:

where Qⁱ denotes the probability that buyer i is awarded the dwelling and Mⁱ denotes the expected payment to the seller. Restated here for convenience, Lopomo (2001) proves the following proposition:

Proposition 1. Given the following assumptions:

A1: Fix any (s₁, …,s_N) ∈ S, pick two elements s_i and s_j, and let s_−ij ∈ [0,1]ⁿ⁻² denote the vector containing the remaining n−2 signals. Then, s_i > s_j implies u (s_i,s_j,s_−ij ≥ u (s_j,s_i,s_−ij)

A2: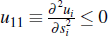

A3: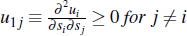

A4: All conditional hazard ratios 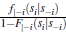are non-decreasing in s_i, where 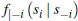and 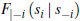denote the distribution and density functions of s_i conditional on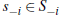

A5: The derivative 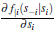exists for all s ∈ S

Then, the optimal seller reserve price, set after n−1 buyers drop out, is given by:

where the function t₀ (s_−i) must satisfy:

Proof. See Lopomo (2001).

Moreover, Lopomo (2001) shows that the seller's expected revenue is maximised among all posterior-implementable and individually rational outcome functions.

A few comments are worth noting at this point. First, Lopomo's assumptions are relevant to the linear example of affiliated values with independent signals that we use. To see this, note that:

which satisfies assumptions A1 to A5. Further, assuming 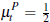and 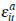is uniformly distributed on [−½, ½], ensures that each signal, s, has a continuous distribution with support [0,1], consistent with Lopomo (2001).

Second, the seller is assumed to be able to set their reserve optimally, after observing the auction proceed until the point at which there is a single buyer remaining. In effect, the seller acts as a buyer in the final stage of the auction competing with the one remaining buyer. In practice this could be implemented through a single vendor bid made at the point at which there is one buyer left in the auction. A single vendor bid is allowed in a standard auction format in NSW and Victoria.

Third, and importantly for our results, the seller's optimal reserve is a function only of the signals of n − 1 buyers who have already exited the auction. This is important, because it suggests that the optimal reserve in effect is determined by buyers' information.

Fourth, solving for the optimal reserve explicitly, in our linear example of affiliated values, we have (applying Proposition 1):

The remaining buyer (with highest signal) will accept this reserve (match the vendor bid) if:

or will otherwise exit the auction.

Accordingly, the effect of introducing an optimal seller reserve is to change the equilibrium price of the auction. The intuition for why this occurs is that the seller knows with positive probability that the remaining buyer is willing to pay more than the price at which the second-last buyer dropped out (recall that the second-last buyer does not observe the signal of the final remaining buyer). For this reason, the seller optimises between the expected gain from placing a higher vendor bid that the remaining buyer may be willing to pay if their signal is high enough, and the expected cost that the vendor bid is too high and the remaining buyer exits the auction (and so the gains from trade are foregone).

In terms of the implications for an individual auction price, with an optimal seller reserve, it follows that the equilibrium price when the auction clears 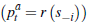, and there are many buyers, converges to

Recall, to be strictly compatible with Lopomo we have assume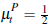d and 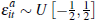. Thus, with an optimal seller reserve price, the average auction price still converges to the common component in all prices up to a scaling factor.

Finally, although we have presented this argument abstracting from a positive seller outside option and have not accounted for the fact that not all dwellings sell when determining average prices, these too can be incorporated. Specifically, there is a significant selection effect that depends on the term 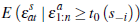. However, again our empirical work suggests that this selection effect is unlikely to be an important driver of changes in auction prices.