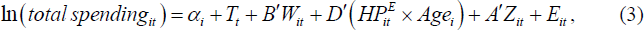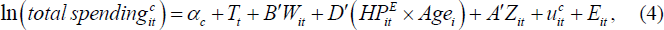RDP 2013-04: Home Prices and Household Spending 4. Results
April 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 732KB
4.1 Household-level Analysis
At the household level, Equation (2) becomes:
where αi are household-fixed effects that control for unobserved time-invariant differences between households and Tt are time-fixed effects. In this specification, we omit dummies for occupation and education from our wealth term since these are typically time-invariant and so are captured by the household-fixed effect.
We estimate the model using the unexplained component of home prices, 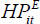 , where the coefficient on home prices is
allowed to vary across age groups (full regression output is given as Model
2 and Model 3 in
Table C1). Figure 4 compares, for our panel of possibly-moving homeowners
(panel two), predicted real spending from this model (dashed lines) to actual
spending (solid lines), using real spending averages over the eight years to
2010 for all households within each age group. This allows us to assess the
functional form of the model by examining whether the life-cycle pattern of
spending follows a hump-shape; such patterns are well-known and widely reported
in the literature – see, for instance, Attanasio and Weber (2010). From
a visual examination it seems that this specification provides a good fit to
the data in the spending-age space for each age group.
, where the coefficient on home prices is
allowed to vary across age groups (full regression output is given as Model
2 and Model 3 in
Table C1). Figure 4 compares, for our panel of possibly-moving homeowners
(panel two), predicted real spending from this model (dashed lines) to actual
spending (solid lines), using real spending averages over the eight years to
2010 for all households within each age group. This allows us to assess the
functional form of the model by examining whether the life-cycle pattern of
spending follows a hump-shape; such patterns are well-known and widely reported
in the literature – see, for instance, Attanasio and Weber (2010). From
a visual examination it seems that this specification provides a good fit to
the data in the spending-age space for each age group.
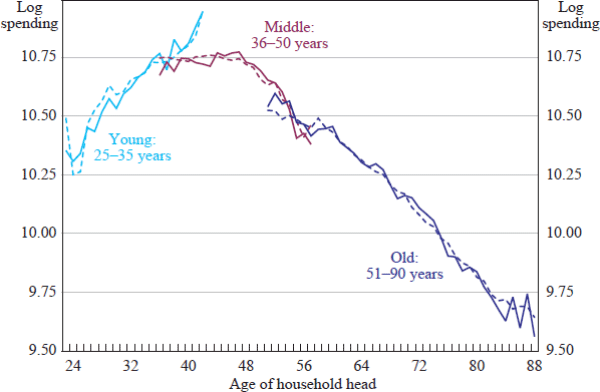
Notes: 2009/10 dollars; deflated using trimmed mean CPI; data are for panel two, defined in Table 1; dashed lines are fitted values; age groups defined in 2003
Sources: HILDA Release 10.0; authors' calculations
The first column of Table 5 shows that home-price wealth effects in panel two are estimated to be largest (and most statistically significant) for young homeowners, at around 4 cents per dollar. For middle-aged and old homeowners we find no significant positive home-price wealth effects. The difference between wealth effects for young and middle-aged homeowners is statistically significant, as is the difference between young and old homeowners. However, there appears to be no statistical difference between wealth effects for middle-aged and old homeowners (Table 5). The second column of Table 5 shows that the age distribution of home-price wealth effects is not sensitive to restricting spending to non-durable items.[15]
| Total spending | Non-durable spending | |
|---|---|---|
| Young | 3.90*** | 3.45*** |
| Middle | 0.10 | 0.35 |
| Old | −0.69* | −0.48 |
| H0: Young = Middle(a) | R*** | R** |
| H0: Young = Old(b) | R*** | R*** |
| H0: Middle = Old(c) | F | F |
|
Notes: R refers to a rejection of the null hypothesis H0, F refers to a failure to reject H0;
***, ** and * indicate significance at the
1, 5 and 10 per cent level, respectively Sources: HILDA Release 10.0; authors' calculations |
||
The finding of large and significant home-price wealth effects for younger households is consistent with the credit constraints hypothesis and the common third factor hypothesis. To distinguish between these hypotheses, the panel with renters is considered (panel one from Table 1). Of course renters do not provide a self-assessed home price. To address this issue, all households were attributed with independent aggregate home prices for their region. The results (see Model 4 in Table C1) show negative but statistically insignificant home-price wealth effects for young renters, and a negative and significant wealth effect for middle-aged renters. This supports the idea that larger estimated wealth effects for younger homeowners reflect credit constraints, rather than a third common factor such as higher expected lifetime earnings being captured by housing prices.
To distinguish our estimated wealth effects from the relationship between housing turnover and spending, the results from Table 5 are re-estimated excluding moving homeowners (panel three from Table 1).[16]
For total spending, dropping moving homeowners decreases estimated wealth effects for young homeowners by less than half of one cent (Table 6 and Model 1 in Table C2). This suggests the turnover effect on spending of young homeowners is not significant. Conversely, wealth effects for middle-aged homeowners increase by around one cent. A middle-aged homeowner's wealth effect is now statistically different to an older homeowner's and, at standard levels of significance, the hypothesis that these effects are the same as those estimated for younger homeowners cannot be rejected.
| Total spending | Non-durable spending | |
|---|---|---|
| Young | 3.67** | 2.54* |
| Middle | 1.00 | 1.35* |
| Old | −0.81** | −0.58 |
| H0: Young = Middle(a) | F | F |
| H0: Young = Old(b) | R*** | R** |
| H0: Middle = Old(c) | R** | R** |
|
Notes: R refers to a rejection of the null hypothesis H0, F refers to a failure to reject H0;
***, ** and * indicate significance at the
1, 5 and 10 per cent level, respectively Sources: HILDA Release 10.0; authors' calculations |
||
4.2 Cohort-level Analysis
In this section, the results are replicated using the synthetic cohort techniques applied by Attanasio et al (2009). While this is a less informative dataset, comparing results at different levels of data aggregation allows the effect of aggregating data on model results to be examined.
This approach controls for unobservable time-constant differences between cohorts rather than households, thereby reducing the number of parameters in Equation (2). Twelve five-year birth cohorts are defined, from before 1926 to 1980, and are entered into Equation (2) as dummy variables (Table 7).
| Cohort dummy | Birth year | Cohort size |
|---|---|---|
| Cohort 1 | 1976 to 1980 | 33 |
| Cohort 2 | 1971 to 1975 | 90 |
| Cohort 3 | 1966 to 1970 | 145 |
| Cohort 4 | 1961 to 1965 | 216 |
| Cohort 5 | 1956 to 1960 | 174 |
| Cohort 6 | 1951 to 1955 | 135 |
| Cohort 7 | 1946 to 1950 | 164 |
| Cohort 8 | 1941 to 1945 | 160 |
| Cohort 9 | 1936 to 1940 | 157 |
| Cohort 10 | 1931 to 1935 | 144 |
| Cohort 11 | 1926 to 1930 | 118 |
| Cohort 12 | Pre-1926 | 67 |
|
Sources: HILDA Release 10.0; authors' calculations |
||
With these cohorts, the model becomes:
where αc are the cohort dummies (for c = 1,…,12)
and 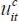 is household
i's deviation from the cohort average. This model implicitly assumes
that the age profile of spending is the same within each cohort (except for
the cohort-specific intercept αc); again our proxy
for wealth includes the highest education level of the household head, the
occupation of the household head, real disposable income, real financial assets
and real housing assets.
is household
i's deviation from the cohort average. This model implicitly assumes
that the age profile of spending is the same within each cohort (except for
the cohort-specific intercept αc); again our proxy
for wealth includes the highest education level of the household head, the
occupation of the household head, real disposable income, real financial assets
and real housing assets.
When estimating Equation (4),
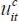 + Eit is treated
as a composite error term which is uncorrelated with the explanatory variables.
When self-assessed home prices are used, however, this assumption becomes tenuous.
It is likely that the cohort dummies, αc, capturing
unobserved cohort heterogeneity, and households' deviations from these
values,
+ Eit is treated
as a composite error term which is uncorrelated with the explanatory variables.
When self-assessed home prices are used, however, this assumption becomes tenuous.
It is likely that the cohort dummies, αc, capturing
unobserved cohort heterogeneity, and households' deviations from these
values,
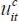 , will be correlated with self-assessed
home prices. In this case, our estimates of home-price wealth effects will
be biased. In light of this, in addition to using self-assessed home prices,
we estimate
Equation (4)
using the unexplained component of aggregate home prices, where for each state we
have a separate home price for capital city dwellings and rest-of-state dwellings.
This breaks the link between a household's home price and any unobserved
household
heterogeneity.[17]
, will be correlated with self-assessed
home prices. In this case, our estimates of home-price wealth effects will
be biased. In light of this, in addition to using self-assessed home prices,
we estimate
Equation (4)
using the unexplained component of aggregate home prices, where for each state we
have a separate home price for capital city dwellings and rest-of-state dwellings.
This breaks the link between a household's home price and any unobserved
household
heterogeneity.[17]
The fit of the model using unexplained aggregate home prices is examined in Figure 5, which compares predicted real spending from Equation (4), averaged across birth cohorts, to actual spending. It seems that this specification provides a good fit to the data within the spending-age space for each cohort (regression output for the model using aggregate home prices is given as Model 1 in Table D1).
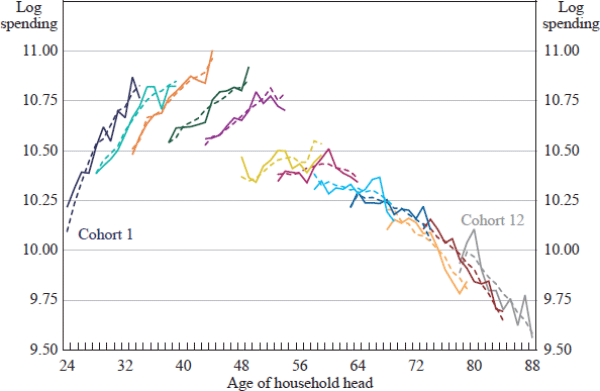
Notes: 2009/10 dollars; deflated using trimmed mean CPI; data are for panel two, defined in Table 1; series represent birth cohorts as defined in Table 7; dashed lines are fitted values
Sources: APM; HILDA Release 10.0; authors' calculations
Table 8 shows the coefficient on unexplained home prices across the age distribution, and, for the model using aggregate home prices, the equivalent coefficients from a household-level regression. In contrast to the results of Table 5, the self-assessed home price results are similar across the age distribution, with home-price wealth effects of around 3 cents per dollar for young and middle-aged homeowners. Older homeowners now show significantly positive wealth effects.
| Cohort regression | Household-level regression | |||
|---|---|---|---|---|
| Self-assessed home prices |
Aggregate home prices |
Aggregate home prices |
||
| Young | 2.76*** | 3.77* | 4.35** | |
| Middle | 3.29*** | 1.35 | 2.78** | |
| Old | 1.88*** | −0.61 | −0.68 | |
| H0: Young = Middle(a) | F | F | F | |
| H0: Young = Old(b) | F | R* | R*** | |
| H0: Middle = Old(c) | F | F | R*** | |
|
Notes: R refers to a rejection of the null hypothesis H0, F refers to a failure to reject H0;
***, ** and * indicate significance at the
1, 5 and 10 per cent level, respectively Sources: APM; HILDA Release 10.0; authors' calculations |
||||
As mentioned earlier, however, these results are likely biased. Replacing self-assessed home prices with an aggregate measure of home prices removes this potential source of bias. Results are shown in the second column of Table 8. These suggest that home-price wealth effects follow a remarkably similar, albeit slightly weaker, pattern to those estimated with household-level data using aggregate home prices (third column of Table 8): young homeowners have higher wealth effects than middle-aged homeowners, who in turn have higher wealth effects than old homeowners. This suggests that ‘pseudo-panels’ are a reasonably good substitute for actual panels. However, point estimates of the age distribution of home-price wealth effects are less precise in the cohort model. A young homeowner's home-price wealth effect is statistically indistinguishable from a middle-aged homeowner's wealth effect which, in turn, is statistically indistinguishable for an old homeowner's wealth effect. Moreover, the use of aggregate home prices appears to inflate estimated wealth effects.
Finally, Table 9 shows home-price wealth effects across the age distribution for the cohort model using aggregate home prices when moving homeowners are dropped from the cohort regression, as well as the equivalent coefficients from a household-level regression. These again show that home-price wealth effects are similar, although slightly weaker in a cohort model, with home-price wealth effects larger for younger homeowners. Dropping moving homeowners gives rise to higher and more precise estimates of the home-price wealth effect across the age distribution, suggesting that moving does indeed change spending in ways that are difficult to control for at the cohort level. Again, the use of aggregate home prices appears to inflate estimated home-price wealth effects.
| Cohort regression Aggregate home prices | Household-level regression Aggregate home prices | |
|---|---|---|
| Young | 6.31*** | 7.30** |
| Middle | 0.57 | 2.23 |
| Old | −0.45 | −0.47 |
| H0: Young = Middle(a) | R** | F |
| H0: Young = Old(b) | R*** | R** |
| H0: Middle = Old(c) | F | R* |
|
Notes: R refers to a rejection of the null hypothesis H0, F refers to a failure to reject H0;
***, ** and * indicate significance at the
1, 5 and 10 per cent level, respectively Sources: APM; HILDA Release 10.0; authors' calculations |
||
Footnotes
The following items are classified as durable: new and used motor vehicles, motorbikes or other vehicles; computers and related devices; televisions, home entertainment systems and other audiovisual equipment; whitegoods such as ovens and fridges; and furniture. [15]
An alternative way to control for the possible effects of moving is to continue to work with panel two (homeowners), but to introduce dummy variables to capture the year of the move as well as any possible level shift in spending post-move. The results from such a model are similar to those already presented – wealth effects for young homeowners are positive and significant, wealth effects for middle-aged homeowners are negative but not significant, while wealth effects for older homeowners are negative and statistically significant. [16]
The same rationale is used by Attanasio et al (2009) to justify using the level of regional housing prices in their analysis rather than homeowners' estimates of the price of their homes, which are available in the UK Family Expenditure Survey data they use. [17]