RDP 2011-06: Does Equity Mispricing Influence Household and Firm Decisions? 6. Robustness
December 2011
- Download the Paper 469KB
id="sec6.1">6.1 Hall Percentile Confidence Intervals
To provide a gauge of the estimation uncertainty surrounding the previous point estimates, I construct 90 per cent confidence intervals for the estimated impulse response functions using a semi-parametric bootstrap (for further detail see Appendix C). Figure 6 reports the bootstrapped confidence intervals using Hall's percentile method, and when each instrument is used in turn as a proxy for mispricing. Two results are noteworthy. First, allowing for estimation uncertainty in this way does not have a substantial effect on the results previously discussed. Mispricing shocks have positive and statistically significant effects on equity prices and consumption, and a negative and significant effect on the quantity of equity held by households irrespective of the instrument used. There is also little evidence of a statistically significant effect of mispricing shocks on household labour income. Again, the results concerning the response of dividends and net worth depend on the instrument used as a proxy for mispricing shocks.
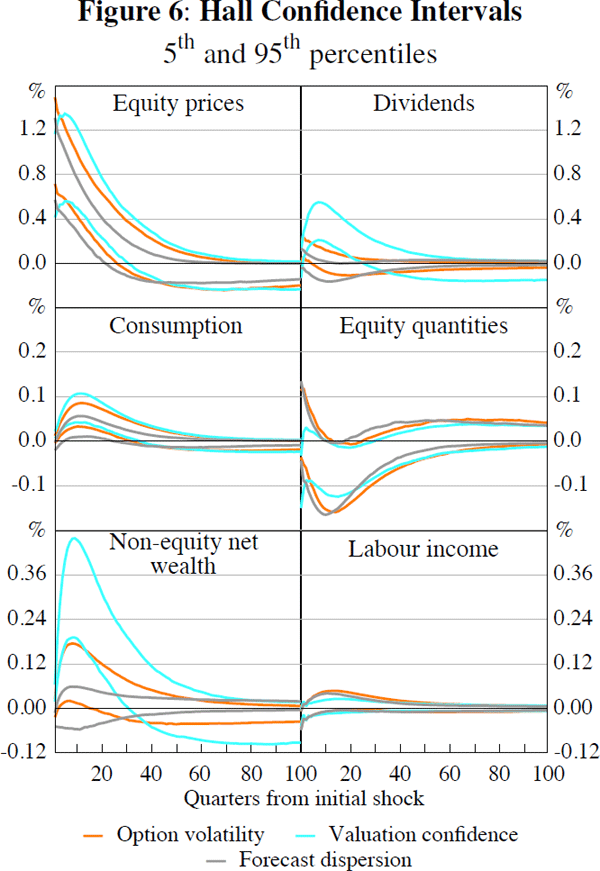
The second point to note is how estimation uncertainty changes when an instrument that is more weakly correlated with equity prices growth is used as a proxy for mispricing shocks. Comparing the width of the confidence intervals produced when valuation confidence, the weakest instrument, is used and the alternative instruments, it is clear that the confidence bands associated with valuation confidence are often wider. Thus, as one would expect, using weaker instruments in the identification procedure does result in greater uncertainty about the estimated impulse response functions.
6.2 Are Weak Instruments a Problem?
As mentioned previously, weak instruments are potentially of concern given the instrument relevance statistics highlighted in Tables 2 and 3. To explore whether weak instruments may be resulting in large finite sample biases, I also use an alternative identification procedure that requires fewer instruments when estimating the system in Equation (9).[48] In particular, by relaxing the restriction that mispricing shocks have only transitory effects, one can estimate the system in such a way that growth in equity prices is the only endogenous variable requiring a valid instrument. This is in contrast to the previous identification method that required valid instruments for both equity prices and equity quantities growth (the two variables directly perturbed by transitory innovations). I refer to the alternative identification procedure that requires fewer instruments as the ‘alternative’ strategy, and that previously used as the ‘benchmark’ strategy.
The advantage of the alternative strategy is that the concern with weak instruments can be mitigated, since only an instrument that is sufficiently correlated with equity prices growth is required. The disadvantage is that this approach is potentially inefficient, since it no longer uses the restriction that mispricing shocks are assumed to have only transitory effects.
Table 6 reports the first-stage results when using the alternative identification strategy. Tests of instrument relevance in this case are able to reject both null hypotheses that the instruments are under-identified and weakly identified when using forecast dispersion and option volatility as instruments, or if both of these measures and valuation confidence are all used collectively. The difference with regard to the previous results, where the null of weak instruments could not be rejected, is that only instruments that are sufficiently correlated with equity prices growth are required when applying the alternative strategy.[49] In contrast, the benchmark method required instruments that are sufficiently correlated with both equity prices and equity quantities growth.
| Forecast dispersion | Option volatility | Valuation confidence | All instruments | |
|---|---|---|---|---|
| CD Wald stat(a)(b) | 11.19 (0.00) |
23.78 (0.00) |
5.40 (0.02) |
47.61 (0.00) |
| CD Wald F-stat(a) | 9.84 | 20.91 | 4.73 | 13.07 |
| Critical value(c) | 8.96 | 8.96 | 8.96 | 4.36 |
| Notes: All statistics are calculated assuming homoskedastic standard errors
(a) Cragg-Donaldson test statistic (b) P-values are in parentheses (c) Based on 15 per cent maximal LIML size |
||||
Figure 7 compares the estimated impulse response functions using the benchmark and alternative identification strategies when using forecast dispersion as the instrument for equity prices growth.[50] Although it can be observed that estimates using the alternative strategy now permit long-run effects in response to mispricing shocks, it is clear that the sign and magnitude of the responses estimated are very similar to those previously identified, and especially so at horizons of less than four years. This similarity suggests that, at least for short-term horizons, the presence of weak instruments under the benchmark strategy is unlikely to be distorting the sign or magnitude of the responses estimated. At longer horizons, the notable differences in the responses estimated suggests that imposing the restriction that mispricing shocks have only transitory effects is important. Without this restriction, estimates of the response to mispricing shocks under the alternative strategy remain noticeably different from zero.
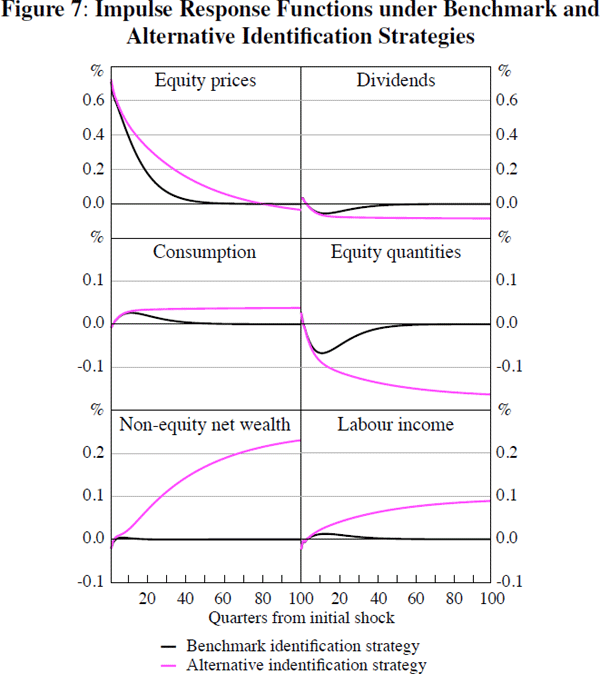
Overall, the similarity of the results obtained when using just-identified IV estimators with different instruments, the relative widths of the bootstrapped confidence intervals, and the similarity in the short-term point estimates under the benchmark and alternative identification strategies, all suggest that weak instruments are unlikely to be resulting in highly misleading inference. Although valid instruments that are more highly correlated with both equity prices and quantities growth would of course be desirable, there does appear to be sufficient information in the instruments proposed for identifying the sign and magnitude of the effects of transitory mispricing shocks.
Footnotes
See Appendix D for further detail. [48]
More specifically, lags of the cointegrating vectors, βyt, are no longer required as instruments. [49]
Results are similar if the other instruments are used. [50]