RDP 2011-06: Does Equity Mispricing Influence Household and Firm Decisions? 4. Empirical Application
December 2011
- Download the Paper 469KB
4.1 Data and Preliminary Analysis
For estimation I use quarterly data for the United States, covering the sample period from June 1986 to December 2006 when either forecast dispersion or option-implied equity volatility are used as instruments for mispricing (the Zt in the methodology described above), or from December 1988 to June 2010 when using the direct survey measure of overvaluation as an instrument. The starting points of these samples reflect data availability on the instruments used for mispricing. The different end points of these samples allow for a comparison of the results with and without the effects of the financial crisis that emerged in 2007.
Following Lettau and Ludvigson (2004), I use household flow consumption of non-durables (excluding clothing and footwear) as a measure of household consumption, and real household after-tax labour income as the measure of income obtained from human capital.[19] Although it would be ideal to use a measure of the total flow services from consumption, excluding durable expenditures, this measure is not directly observed.[20] To measure the cost of purchasing a unit of US equity (equity prices) I use the share price of Vanguard's S&P 500 ETF measured at the end of the quarter.[21] This measure provides a good proxy for the cost of purchasing a diversified equity portfolio that replicates the US S&P 500. I use a seasonally adjusted quarterly dividend measure, also measured with respect to the US S&P 500.
US Flow of Funds Accounts data are used to separate US household net financial wealth into its domestic equity and non-domestic-equity components. I focus on domestic equity because I am interested in studying the effects of mispricing in the US equity market.[22] To construct a measure of household wealth held in US equity, I multiply total household equity holdings (which includes both domestic and foreign components) by the proportion of equity held by all sectors (households and corporate) in US equity. This assumes that the household portfolio share allocations to domestic and foreign equity are similar to the allocations held across the total US private sector.[23] Household non-US-equity net wealth (hereafter non-equity net wealth) is a residual defined as total household net financial wealth less holdings of domestic equity. To construct an internally consistent measure of the quantity of equity held by US households (equity quantities), I divide the domestic equity holdings measure by the share price measure defined above.[24]
In terms of observable information used to distinguish between fundamental and non-fundamental transitory shocks, I consider three measures. The first is a measure of analyst forecast dispersion with respect to the US S&P 500, obtained from the Institutional Brokers' Estimate System (I/B/E/S). Specifically, I use the weighted average standard deviation of analysts long-term average growth in earning per share forecasts for the US S&P 500.[25] The second instrument considered is a measure of option-implied equity volatility. In particular, I use implied 30-day volatility for the US S&P 100 as traded on the Chicago Board Options Exchange (with ticker VXO). I use this measure because longer time series are available than for implied 30-day volatility for the US S&P 500 (the VIX), but both measures are highly correlated and the results obtained are not sensitive to this choice over a common sample. The third measure I use is a direct survey measure of perceived over-valuation in the US equity market obtained from surveys of US institutional investors and sourced from the Yale School of Management (see also Shiller (2000b)).[26] The rationale for using each of these measures as instruments for equity prices growth is discussed further below.
Consumption, non-equity net wealth, equity quantities and real after-tax labour income are all in per capita log terms, and data on equity prices and dividends are in log terms. All data, with the exception of equity quantities, consumption and the instruments for mispricing, are deflated by the US personal consumption expenditure deflator.[27] All data used in estimation are measured at a quarterly frequency.
Before proceeding with the proposed identification methodology, it is important to establish that a cointegration framework is in fact a suitable representation of the data. For pre-testing I use all available data on the endogenous variables (yt) from March 1953 to June 2010, to ensure accurate inference. Unit root tests are consistent with each of the data series being I (1), and standard information criteria are consistent with two lags in a levels VAR (a VECM with a single lag). Tests of whether the data are cointegrated (the rank of the cointegration matrix) suggest two cointegrating vectors in the data.[28] All pre-testing results are reported in Appendix B.
Turning to estimation of the cointegration matrix, 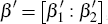 ,
I restrict attention to the main samples used for estimation, from June 1986
to December 2006 and December 1988 to June 2010. Since it is well known that
cointegration estimates are more precise if all known information is used by
the researcher in estimation, I restrict the second cointegrating vector to
have one and minus one coefficients on dividends and equity prices respectively,
,
I restrict attention to the main samples used for estimation, from June 1986
to December 2006 and December 1988 to June 2010. Since it is well known that
cointegration estimates are more precise if all known information is used by
the researcher in estimation, I restrict the second cointegrating vector to
have one and minus one coefficients on dividends and equity prices respectively,
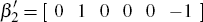 .
This implies that the log dividend to equity price ratio is stationary, which
is consistent with the theory described above and is a common assumption that
has been used in previous empirical
research.[29]
.
This implies that the log dividend to equity price ratio is stationary, which
is consistent with the theory described above and is a common assumption that
has been used in previous empirical
research.[29]
Estimating the cointegration matrix, subject to the above restriction, the first
cointegrating vector has coefficients 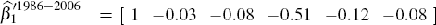 in the sample
from June 1986 to December 2006, and
in the sample
from June 1986 to December 2006, and 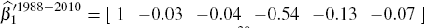 in the sample
from December 1988 to June
2010.[30]
These coefficients are consistent with economic theory, with human capital
estimated to be the largest share of wealth, and the sum of the coefficients
on equity prices and dividends being almost identical to the coefficient on
equity quantities (as implied by the previous theoretical motivation). These
estimates are also comparable to estimates of the same cointegrating relationship
– that do not distinguish between the US equity and non-US equity components
of wealth – using single-equation methods, see, for example, Lettau
and Ludvigson (2004). In the analysis that follows, I use
in the sample
from December 1988 to June
2010.[30]
These coefficients are consistent with economic theory, with human capital
estimated to be the largest share of wealth, and the sum of the coefficients
on equity prices and dividends being almost identical to the coefficient on
equity quantities (as implied by the previous theoretical motivation). These
estimates are also comparable to estimates of the same cointegrating relationship
– that do not distinguish between the US equity and non-US equity components
of wealth – using single-equation methods, see, for example, Lettau
and Ludvigson (2004). In the analysis that follows, I use  as a consistent estimate
of the true cointegration space of the data in each sample, identified up
to a non-singular transformation.
as a consistent estimate
of the true cointegration space of the data in each sample, identified up
to a non-singular transformation.
4.2 Identification
In view of the fact that the estimation methodology in Section 3 relies on IV techniques, it is important to establish that the instruments used are both relevant and valid.[31] This is especially so for the instruments used for equity prices growth, that enable identification of fundamental and non-fundamental transitory shocks. I first address the question of instrument relevance, before turning to the issue of validity, for each of the instruments in turn.
The rationale for forecast dispersion being correlated with bubbles is that greater heterogeneity in analysts expectations could be consistent with mispricing in equity markets if some analysts are unable (or unwilling) to execute trades that reflect this greater divergence of opinion. For example, a constraint on short-selling is one frequently cited market or institutional constraint that would be consistent with greater heterogeneity implying equity mispricing (see, for example, Diether et al (2002) and the references cited therein). However, other explanations such as the existence of heterogenous investors, including rational and non-rational investors, and the inability of rational investors to co-ordinate their actions could also imply a correlation between forecast dispersion and mispricing (see, for example, Shleifer and Vishny (1997); Abreu and Brunnermeier (2003)). Furthermore, heterogenous optimism (Brunnermeier and Parker 2005), and the incentive for informed advisors to inflate their forecasts of fundamentals (Hong, Scheinkman and Xiong 2008), are also economic environments that can support a correlation between forecast dispersion and mispricing in the equity market.
In terms of exogeneity, Diether et al (2002) and Gilchrist et al (2005) argue that forecast dispersion is unlikely to be correlated with the fundamental investment opportunities available to firms. The underlying assumption is that shocks that affect mean forecasts for earnings and equity prices are not systematically correlated with shocks to the variance of these forecasts. For example, Diether et al (2002) provide evidence supporting the view that forecast dispersion in earnings per share is a useful instrument for equity prices growth in the US context. These authors highlight that on average companies with higher forecast dispersion for their earnings tend to have low future returns. According to the authors, this pattern is consistent with an interpretation where over-confidence or over-optimism on the part of some investors can lead to overpricing when combined with market, institutional or information constraints on non-optimistic investors. Alternatively, such a correlation is inconsistent with an interpretation where fundamental shocks to uncertainty are driving the correlation between equity prices growth and forecast dispersion.
Gilchrist et al (2005) also use forecast dispersion as an instrument for mispricing in the US equity market. They argue that forecast dispersion is a better measure of mispricing than other proxies for bubbles that have been suggested in previous literature, such as lagged prices or market to book valuations. The latter measures are thought more likely to be affected by the investment opportunities available to firms, and thus are more likely to be correlated with fundamental shocks.[32]
Turning to the survey measure of valuation confidence compiled by the Yale School of Management, and discussed in Shiller (2000b), this measure is also likely to be correlated with mispricing in the US equity market. This measure reflects a survey of US institutional investors undertaken biannually until July 2001, and at a monthly frequency thereafter.[33] Institutional investors are asked the following question:
‘Stock prices in the United States, when compared with
measures of true fundamental value or sensible investment value,
are: [CIRCLE ONE NUMBER]
1. Too low. 2. Too high. 3. About right. 4. Do not know.’
The responses are designed to provide a direct gauge on whether institutional investors perceive US equity markets as being priced correctly, or whether they are undervalued or overvalued.[34] The exogeneity of this measure is largely assured due to survey design. Shiller (2000b) argues that the wording of this question is informative about potential mispricing in the market, because it explicitly asks survey respondents on their views of valuation controlling for their own knowledge or assessment of market fundamentals.[35] Rather than asking institutional investors whether they expected prices to rise or fall, as some other survey measures that would be correlated with fundamentals do, the survey asks respondents directly about valuation in relation to fundamentals, and whether they perceive the current market as being ‘too low’ (undervalued), ‘too high’ (overvalued) or ‘about right’ (fair value).
The third instrument considered is option-implied equity volatility. Conceptually, this derivative is a measure of market expectations concerning future short-term volatility in a share market index. One might expect that during bubble episodes mispricing in equity markets could be correlated with expected volatility in the index. This could occur if some investors use trading strategies that are based on volatility to profit from bubbles. For example, if informed investors consider the market to be over-valued, but are unable to time exactly when a price correction is likely, then a trading strategy that pays high when markets are expected to move strongly in either direction may be a more profitable risk-adjusted strategy than taking short or long positions on a bubble directly.
Nonetheless, whether short-term option-implied volatility is uncorrelated with fundamental shocks is less clear on theoretical grounds. Although implied volatility may be uncorrelated with conventional fundamental shocks, such as shocks to firm productivity or household preferences, it could be argued that movements in short-term volatility could be correlated with short-term uncertainty that is fundamental in nature. For example, shocks such as terrorism attacks, wars, or uncertainty about major policy changes that affect US corporate profitability could be regarded as fundamental short-term volatility shocks that affect option-implied volatility, and potentially other economic variables of interest (see, for example, Bloom (2009)). This suggests that using this third instrument, in conjunction with the identification strategy proposed, may result in inference that is not able to distinguish between the effects of fundamental uncertainty shocks that have transitory effects, and mispricing.
With this caveat in mind, I test whether this third instrument is valid, conditional on either forecast dispersion, or valuation confidence being valid instruments. If it is true that fundamental uncertainty shocks are important in the sample under consideration, and these are correlated with the other permanent or transitory shocks in this system, one would expect option-implied volatility to fail instrument orthogonality tests. Table 1 reports the results of Hausman tests that are robust to the presence of weak instruments.[36] The null hypotheses considered are that each of the permanent shocks are individually uncorrelated with option volatility, and that a linear combination of the permanent shocks and the fundamental transitory shock is also uncorrelated with option volatility.[37] The results in Table 1 highlight that these null hypotheses cannot be rejected at standard significance levels, and so they are consistent with option volatility being a valid instrument for equity prices growth.[38]
| Equation | Hausman test statistic | Hausman test statistic |
|---|---|---|
| Consumption(a) | 0.05 | 0.04 |
| Dividends(a) | 0.04 | 0.01 |
| Non-equity net wealth(a) | 1.62 | 0.85 |
| Labour income(a) | 0.01 | 0.06 |
| Equity quantities(b) | 0.04 | 0.40 |
| Critical value(c) | 3.84 | 3.84 |
| Exogenous instruments | β1yt – 1(a) Forecast dispersion(a), (b) |
β1yt – 1(a) Valuation confidence(a), (b) |
| Sample | Jun 1986 to Dec 2006 | Dec 1989 to Jun 2010 |
Notes: (a) The null hypothesis is  vs the alternative vs the alternative
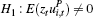 (b) The null hypothesis is 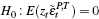 vs the alternative vs the alternative 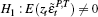 (c) Obtained from a Chi-squared distribution with one degree of freedom, and at the 5 per cent level of significance |
||
An additional reason to think that option volatility is a valid instrument in the current context is due to the sample under consideration. Although fundamental uncertainty shocks are likely to be relevant in the period following the financial crisis that began in 2007–2008, the importance of these shocks is less clear in the sample from June 1986 to December 2006. In particular, one would have to justify why option-implied volatility drifted upwards from June 1995 to March 2000 (see Figure 1), at the same time that equity prices in the United States grew substantially. Such a result is inconsistent with typical fundamental explanations of volatility, which usually suggest that higher volatility should be associated with greater fundamental uncertainty, lower investment and lower equity prices.
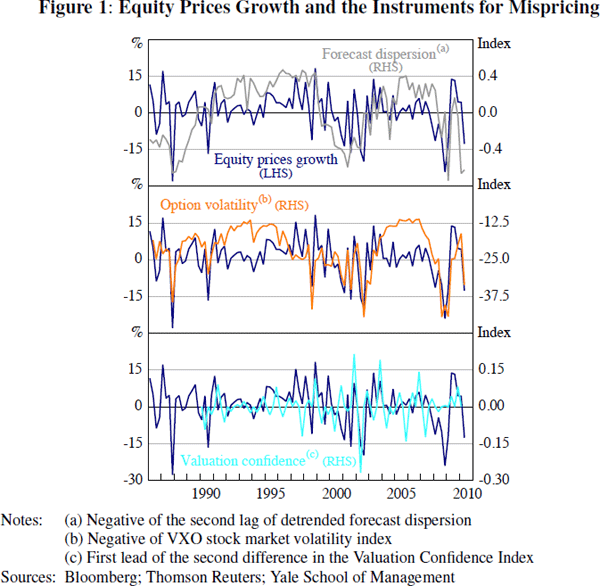
I now address whether these instruments are relevant from an empirical perspective. Figure 1 reports a graph of equity prices growth compared with each of the three candidate instruments – the second lag of detrended forecast dispersion, contemporaneous option-implied equity volatility, and the first lead of the second difference of the valuation confidence index. These instruments are selected because they have the highest reduced-form correlations with equity prices growth. I use detrended forecast dispersion to account for the upwards drift in earnings per share over time. The second difference, or change in momentum, of valuation confidence is used because it ensures that only information at a biannual frequency is actually used in estimation.[39]
Figure 1 highlights that all three variables appear to exhibit some correlation with equity prices growth, a result that is investigated more formally below. Forecast dispersion and option volatility appear to be most highly correlated with equity prices growth, although all three measures are consistent with an increase in forecast dispersion, uncertainty and concerns of overvaluation in the late 1990s. This preceded the sharp deceleration in prices growth observed in 2000.
Table 2 reports the results from first-stage regressions, and formal tests for instrument relevance, with respect to the permanent equations in Equation (14). To be clear, the two relevant first-stage regressions are of the form
for j = 1, 2, where ξ1t – 1 = β1yt – 1, and zt is one of the candidate instruments.
| Forecast dispersion | Option volatility | Valuation confidence | |
|---|---|---|---|
| Equity quantities F-stat | 2.76 3.32 |
2.77 3.26 |
1.71 2.09 |
| Equity prices F-stat | 5.41 3.60 |
11.09 7.66 |
2.10 2.28 |
| CD Wald stat(a)(b) | 4.67 (0.03) |
5.50 (0.02) |
3.28 (0.07) |
| CD Wald F-stat(a) | 2.11 2.08 |
2.37 2.45 |
1.47 1.46 |
| Critical value(c) | 3.63 | 3.63 | 3.63 |
| Notes: Statistics in italics are computed with robust standard errors (a) Cragg-Donaldson test statistic (b) P-values are in parentheses (c) Based on 25 per cent maximal LIML size and assuming homoskedastic errors |
|||
The results are highlighted when using each candidate instrument in turn. The first test for relevance considered is that the instruments are under-identified. Essentially, it is a test of whether the excluded instruments, ξ1t – 1 and zt, are sufficiently correlated with the endogenous regressors, Δy21,t and Δy22,t, for meaningful IV inference to be undertaken. Using the Cragg-Donaldson Wald statistic (rows 5 and 6), the null that the instruments are under-identified can be rejected at conventional significance levels.[40]
Although tests for the null of under-identification can be rejected, tests of the null that the instruments are only weakly correlated with the endogenous regressors cannot be rejected at conventional significance levels. In particular, using the test for weak instruments proposed by Stock and Yogo (2005), the critical values published by Stock and Yogo are greater than the relevant Cragg-Donaldson Wald F-statistics (rows 7 to 9). Moreover, F-statistics associated with the first-stage regressions for each of the instruments suggest that weak instruments could be a concern, especially with respect to the equity quantities measure (rows 1 to 2).
In view of the concern associated with weak instruments for these first-stage regressions, I use two strategies in the analysis that follows. The first is to use just-identified IV estimators, using each of the candidate instruments in turn. There is research suggesting that just-identified estimators can be viewed as approximately median-value unbiased with weak, though identified, instruments.[41] The second strategy, followed in Section 6, is to consider an alternative approach to estimation of the system in Equation (12) that requires fewer instruments in the procedure used to identify the mispricing shock. By reducing the number of endogenous variables, specifically eliminating the need to instrument for the measure of equity quantities, tests of the null that the instruments are weak can be rejected at conventional significance levels. As discussed in Section 6, the results using either strategy are comparable at short- to medium-term horizons.
Proceeding using the just-identified IV estimators, first-stage tests for instrument relevance in the transitory equation for equity quantities are obtained from the following first-stage regressions
where 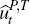 are the residuals obtained from IV estimates of the permanent equations. Table 3
highlights that when using these residuals and each of the proxies for mispricing
shocks as instruments (in turn), first-stage F-statistics are large and the
null that these instruments are under-identified can be rejected at conventional
significance
levels.[42]
Nonetheless, it should be noted that the F-statistics that provide a measure
of the correlation between the excluded instruments and equity prices growth,
rows 9 and 10, remain in a range where weak instruments could be a concern.
I next present point estimates based on the just-identified IV estimators,
before turning to the question of whether concerns associated with weak instruments
are likely to be biasing these point estimates.
are the residuals obtained from IV estimates of the permanent equations. Table 3
highlights that when using these residuals and each of the proxies for mispricing
shocks as instruments (in turn), first-stage F-statistics are large and the
null that these instruments are under-identified can be rejected at conventional
significance
levels.[42]
Nonetheless, it should be noted that the F-statistics that provide a measure
of the correlation between the excluded instruments and equity prices growth,
rows 9 and 10, remain in a range where weak instruments could be a concern.
I next present point estimates based on the just-identified IV estimators,
before turning to the question of whether concerns associated with weak instruments
are likely to be biasing these point estimates.
| Forecast dispersion | Option volatility | Valuation confidence | |
|---|---|---|---|
| Consumption F-stat | 17.85 11.40 |
13.23 12.98 |
16.45 15.11 |
| Dividends F-stat | 55.77 54.24 |
51.82 47.59 |
231.32 209.17 |
| Non-equity net worth F-stat | 108.70 60.00 |
7.5 × 104 1.6 × 105 |
33.54 36.09 |
| Labour income F-stat | 142.88 160.69 |
145.73 168.64 |
210.13 295.70 |
| Equity prices F-stat | 7.14 4.54 |
7.48 4.88 |
4.89 3.86 |
| CD Wald stat(a)(b) | 8.90 (0.00) |
16.90 (0.00) |
4.62 (0.03) |
| Notes: Statistics in italics are computed with robust standard errors (a) Cragg-Donaldson test statistic (b) P-values are in parentheses |
|||
Footnotes
For a more detailed description of the data, see Appendix A. [19]
See Lettau and Ludvigson (2004) for further discussion. [20]
The results are very similar if the US S&P 500 index is used. [21]
The preceding theoretical discussion can be appropriately modified to account for the fact that US households own both domestic and foreign equity. [22]
This assumption is required since data on domestic and foreign equity portfolio allocations are only reported for all US sectors, and not specifically for households. [23]
Both the non-equity net wealth and equity quantities measures are lagged one quarter to be consistent with their beginning of period values used in the theory previously discussed. [24]
This index is constructed by weighting the standard deviation of analyst forecasts (of long-term average growth in earnings per share) for each firm in the US S&P 500. The weights used reflect the market capitalisation of each firm in the total index. [25]
I am most grateful to Robert Shiller and the Yale School of Management for making these data available. [26]
Consumption of non-durables (excluding clothing and footwear) is deflated by its own implicit price deflator. See Lettau and Ludvigson (2004) for further detail. [27]
Rank tests yield similar results if performed on the main estimation sample, from June 1986 to December 2006. All tests allow for an unrestricted constant in the cointegration model. [28]
See, for example, Campbell and Shiller (1987), Cochrane (1994) and Lee (1998) amongst others. [29]
Specifically, I use FIML (Johansen's approach), subject to the restrictions that
the rank of β is two and that 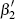 is known. The coefficients
in β1 are identified up to a linear scaling factor.
[30]
is known. The coefficients
in β1 are identified up to a linear scaling factor.
[30]
Sarte (1997) provides a useful discussion in the context of structural vector autoregressions. [31]
For additional surety, I use a measure of forecast dispersion with regard to average long-term growth in earnings per share. This should help to ensure that dispersion is not being driven by fundamental shocks relating to near-term uncertainty. [32]
When used in estimation, quarterly data are interpolated from the biannual data prior to July 2001. [33]
The Yale School of Management measure reports the Valuation Confidence Index as the number of respondents who choose 1 or 3 as a percentage of those who chose 1, 2 or 3. I use one minus this percentage in subsequent empirical analysis. [34]
There is an extensive literature in behavioural finance documenting potential market, institutional or information impediments that can sustain such mispricing, even when certain classes of investors feel confident that current market conditions are consistent with a bubble. See, for example, Shiller (2000a). [35]
See Hahn, Ham and Moon (2011). [36]
Refer to Appendix D for the appropriate regression specification in the latter case. [37]
Additional tests for conditional validity, for example of forecast dispersion being valid conditional on valuation confidence being valid, also fail to reject the hypothesis that both instruments are valid. Results are available on request. [38]
Recall that valuation confidence prior to July 2001 is only measured at a biannual frequency. Using the second difference, on a quarterly linear interpolation, in effect implies that only the change in momentum measured at six-monthly intervals is used. Under relatively weak assumptions, this measure will provide consistent IV estimates. [39]
Although the lagged dividend to equity price ratio, 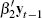 ,
is also a valid instrument in the first stage, this instrument was found
only to be weakly correlated with equity prices growth and is not therefore
used when applying IV.
[40]
,
is also a valid instrument in the first stage, this instrument was found
only to be weakly correlated with equity prices growth and is not therefore
used when applying IV.
[40]
See, for example, Angrist, Imbens and Krueger (1999) and Angrist and Pischke (2009). [41]
Results are qualitatively similar for the transitory equation for equity prices, and are available on request. [42]