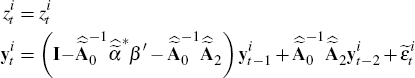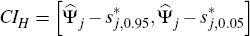RDP 2011-06: Does Equity Mispricing Influence Household and Firm Decisions? Appendix C: Bootstrap Methodology
December 2011
- Download the Paper 469KB
90 per cent confidence intervals are constructed using the following semi-parametric bootstrap procedure:
-
Using the procedure outlined in Section 3,
I obtain estimates of the semi-structural residual vector
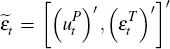conditioning on 
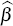and the instruments 
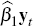and zt (recall zt
is the relevant instrument for mispricing shocks, either forecast dispersion,
option volatility or valuation confidence).
-
Randomly draw with replacement (by column) from the matrix of estimation residuals
and
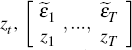, so that in effect a form of ‘pairs’
bootstrap is used that accounts for the joint empirical distribution of the
errors and the instrument used in identification. One thousand random samples
of length T = 83 are drawn.
-
Simulate data to construct the vector
using
for t = 1, …, T and for i = 1, …, 1,000 where i is an index identifying the relevant draw in Step 2, and where
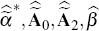are the point estimates used to construct the statistics of interest discussed in
the main
text.[53]
-
For each artificial sample, i, estimate
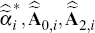and then construct
the estimated impulse response function (moving average) matrices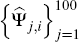 
for i = 1,…,
1,000. Note that 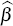is treated as known and is not re-estimated
with each sample.
-
Construct Hall percentile confidence intervals following Lütkepohl (2006). Let
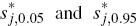be the 5 and 95 percentiles of the statistic 
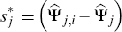where 
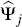is the estimated
impulse response function based on the observed data, j quarters
after the initial shock of interest. The Hall confidence interval is given
by
Footnote
For brevity, I abstract from deterministic terms. In implementation I allow for an unrestricted constant in the SVECM. [53]