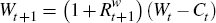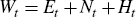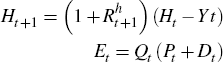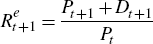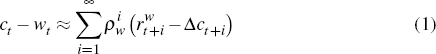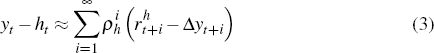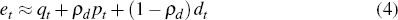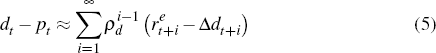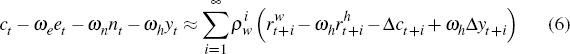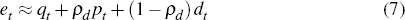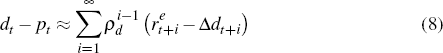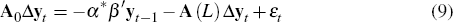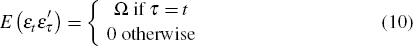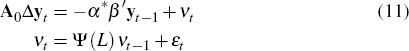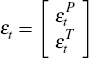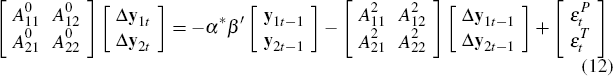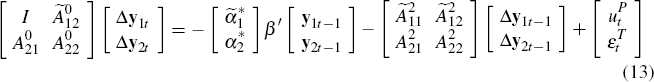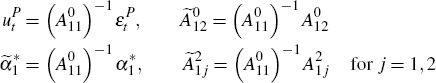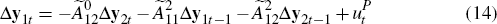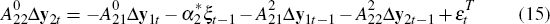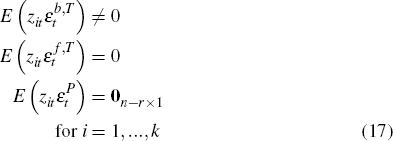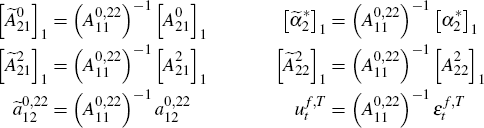RDP 2011-06: Does Equity Mispricing Influence Household and Firm Decisions? 3. Estimation Methodology
December 2011
- Download the Paper 469KB
I use two ideas to identify the effects of equity mispricing. The first is that equity mispricing should only have transitory economic effects (see, for example, Lee (1998)). Such an assumption appears reasonable from a theoretical standpoint, given that many economists have the prior that equity prices are not entirely disconnected from the fundamental processes underpinning the economy. If the converse were true, and mispricing shocks had permanent effects, then equity prices would effectively be indeterminate and have no relationship with the underlying value of the dividend streams they pay.
The second idea is that there is observable information that can be used to distinguish between fundamental and non-fundamental transitory shocks. This reasoning follows a recent literature which argues that there are observables that are correlated with equity market mispricing, and that are uncorrelated with measures of economic fundamentals, see, for example, Diether et al (2002) and Gilchrist et al (2005).
I use these two ideas, in conjunction with a cointegration framework implied by economic theory, to identify the effects of equity mispricing shocks. More specifically, I use five economic relationships to motivate the empirical work in this paper. The first is an accumulation equation for aggregate household wealth
where Wt is beginning of period wealth, Ct
is total flow consumption in the period, and 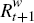 is the return to total
wealth. This formulation assumes that the market value of human capital is
tradeable and included in aggregate wealth. This assumption simplifies exposition,
but is an assumption that can be relaxed without substantively affecting any
of the analysis that follows (see Lettau and Ludvigson (2004)). The second
relationship used is that household wealth can be decomposed into its respective
equity, non-equity, and human capital components
is the return to total
wealth. This formulation assumes that the market value of human capital is
tradeable and included in aggregate wealth. This assumption simplifies exposition,
but is an assumption that can be relaxed without substantively affecting any
of the analysis that follows (see Lettau and Ludvigson (2004)). The second
relationship used is that household wealth can be decomposed into its respective
equity, non-equity, and human capital components
where Et is total equity wealth held by households, Nt is total non-equity wealth (such as housing, consumer durables, and other forms of financial non-equity wealth), and Ht is human capital. The third and fourth relationships used are an accumulation equation for tradeable human capital, and the definition of equity wealth
where 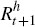 is the return to human capital, Yt is labour income, Qt
is the quantity of equity held, Pt is the ex-dividend price
of equity, and Dt is the dividend paid on equity held in
period t. The final relationship used is the definition of the return to equity,
is the return to human capital, Yt is labour income, Qt
is the quantity of equity held, Pt is the ex-dividend price
of equity, and Dt is the dividend paid on equity held in
period t. The final relationship used is the definition of the return to equity,
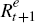 ,
where
,
where
Using arguments that are similar to those used by Campbell and Mankiw (1989), Lettau and Ludvigson (2004, 2005) and Kishor (2007), I log-linearise these relationships, assuming a balanced growth path, and obtain the following economic system[7]
where lower case variables denote natural logarithms,[8] ωe, ωn and ωh are the steady state shares of equity, non-equity and human capital wealth in total wealth respectively, ρw is the steady state share of savings in total wealth, ρh is one minus the share of labour income in steady state human capital, and ρd is the steady state ratio of the ex-dividend equity price to the equity price that includes dividends. It should be noted that the system defined by Equations (1) to (5) contains two variables that are not directly observable, human capital wealth and total household wealth. To account for this, I substitute human capital and total wealth out of the above system to obtain[9]
Assuming that consumption, the quantity of equity held, non-equity wealth, equity prices, labour income, and dividends are integrated of order one, and that returns to total financial wealth, human capital wealth and equity wealth are stationary, it follows that Equations (6) to (8) make up a cointegrated system with two cointegrating vectors.
It should be made clear that Equations (6) to (8) make up a partially specified economic system. Additional model structure, for example including an Euler equation for consumption or an equity pricing equation, could potentially imply more restrictions or additional cointegrating relationships in this system. I choose not to include such structure given existing disagreement over the ‘correct’ model for either consumption or equity prices. Instead, I use the above framework as a motivation for modelling a system consistent with Equations (6) to (8), and use empirical analysis to determine the number of cointegrating relationships. I do not impose any model-specific restrictions that could otherwise be incorporated.
A general econometric representation that is consistent with Equations (6) to (8) is the structural vector error correction model (SVECM)
where yt is an n × 1 vector of observables, yt = [ ct dt nt yt qt pt ]′, A(L) is a lag polynomial of order l, β′ is the matrix of cointegrating vectors, and α* the matrix of loading coefficients on the cointegrating vectors.[10] I assume A0 is non-singular and that α*β′ has rank r < n so that at least one cointegrating vector exists. The εt are the primitive structural shocks. I assume these shocks are independently identically distributed, with E (εt) = 0 and
where Ω is a diagonal matrix (with elements that are not necessarily equal).[11] The εt are the underlying structural shocks that I am in interested in identifying. Specifically, I wish to identify the elements of εt that only have transitory effects, and in particular, non-fundamental transitory effects.
It should be noted that the structural shocks being serially uncorrelated is not necessarily a restrictive assumption in the current context. In particular, Equation (9) can be viewed as a finite-order approximation of a model in which the structural shocks are serially correlated (see, for example, Lütkepohl (2006)). That is, Equation (9) can be viewed as an approximation of a SVECM with moving average errors,
where Ψ(L) is an infinite-order lag polynomial. In this model, transitory mispricing disturbances in νt can be serially correlated with permanent shocks to fundamentals, an assumption that is consistent with the idea that permanent shocks to fundamentals, such as permanent changes in technology, can precede mispricing in the equity market. In the analysis that follows, I focus on estimating Equation (9), which can be interpreted as a finite-order approximation of Equation (11).[12]
3.1 Identification of Reduced-form Shocks
To distinguish between the reduced-form transitory and permanent shocks in Equation (9), I follow a re-parameterisation of the approach to identification suggested by Pagan and Pesaran (2008). Without loss of generality, I order the permanent and transitory shocks according to
where 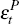 is a (n – r) × 1 vector of shocks with permanent effects
is a (n – r) × 1 vector of shocks with permanent effects
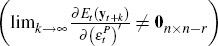 ,
and
,
and 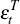 is a r × 1 vector of shocks that have transitory effects
is a r × 1 vector of shocks that have transitory effects 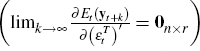 .[13]
Since I assume that mispricing shocks have only transitory effects on the system,
a mispricing shock must be an element of
.[13]
Since I assume that mispricing shocks have only transitory effects on the system,
a mispricing shock must be an element of 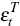 .
.
I proceed by estimating Equation (9) using limited information methods. The first
step is to obtain a consistent estimate of the cointegrating matrix, β (or use the known cointegration matrix in the case that β
is known). Importantly, as emphasised by Pagan and Pesaran, only a consistent
estimate of the cointegration space – the column space of β,
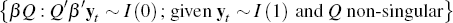 – is required since the instrumental variable (IV) methods
described below are invariant to non-singular transformations. A consistent
estimate of this space can be obtained, for example, from the Johansen full
information maximum likelihood (FIML) estimates of the reduced
form of Equation (9) or using alternative system methods discussed by Lütkepohl
(2006).
– is required since the instrumental variable (IV) methods
described below are invariant to non-singular transformations. A consistent
estimate of this space can be obtained, for example, from the Johansen full
information maximum likelihood (FIML) estimates of the reduced
form of Equation (9) or using alternative system methods discussed by Lütkepohl
(2006).
Assuming a consistent estimate of β is available, I partition Equation (9) into a system of n
– r equations with permanent shocks, 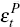 , and r remaining
equations with transitory shocks
, and r remaining
equations with transitory shocks 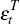
and I assume, without loss of generality, that A(L) = A2L. This assumption abstracts from lag dynamics that do not affect the generality of the identification approach proposed.
Since I previously assumed 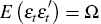 ,
where Ω is a diagonal matrix, I impose n normalisation restrictions
on the main diagonals of
,
where Ω is a diagonal matrix, I impose n normalisation restrictions
on the main diagonals of 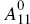 and
and 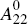 . I further assume that
. I further assume that
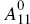 is non-singular. With these assumptions, a simple matrix premultiplication yields
is non-singular. With these assumptions, a simple matrix premultiplication yields
where
The above premultiplication is useful because it allows identification of transitory
shocks, without requiring identification of the permanent shocks to the system.
That is, I only identify linear combinations of the permanent shocks, 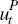 ,
and not the underlying permanent structural shocks,
,
and not the underlying permanent structural shocks, 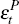 .
.
Using the result that lagged error correction terms should not be present in the
structural permanent equations, 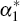 =
0,[14]
one can use these restrictions to estimate the first n – r
permanent equations in Equation (13). Specifically, this set of restrictions
implies that the r × 1 vector ξt – 1
= β′yt – 1 can
be used as instruments for the vector Δy2t.
And so, the first n – r permanent equations
=
0,[14]
one can use these restrictions to estimate the first n – r
permanent equations in Equation (13). Specifically, this set of restrictions
implies that the r × 1 vector ξt – 1
= β′yt – 1 can
be used as instruments for the vector Δy2t.
And so, the first n – r permanent equations
can be estimated using standard IV methods. This provides consistent estimates of
the reduced-form matrices 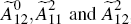 ,
and the reduced-form permanent shocks,
,
and the reduced-form permanent shocks, 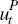 .
.
To estimate the remaining r transitory equations
I can now use the consistent estimates, 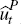 ,
as instruments for the endogenous variables in Δy1t
(see Pagan and Pesaran (2008)). This would enable identification of the reduced-form
transitory shocks,
,
as instruments for the endogenous variables in Δy1t
(see Pagan and Pesaran (2008)). This would enable identification of the reduced-form
transitory shocks, 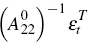 , but to identify the structural transitory
shocks,
, but to identify the structural transitory
shocks, 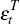 ,
it is clear that additional restrictions are required.
,
it is clear that additional restrictions are required.
3.2 Identification of Structural Transitory Shocks
Focusing on the transitory equations in Equation (15), recall that I have already
imposed r normalisation (unity) restrictions on the main diagonal of 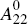 .
Since I have previously assumed that transitory shocks are
uncorrelated (see Equation 10), this implies that an additional r
(r – 1)/2 additional restrictions are required to be able to
identify the structural shocks,
.
Since I have previously assumed that transitory shocks are
uncorrelated (see Equation 10), this implies that an additional r
(r – 1)/2 additional restrictions are required to be able to
identify the structural shocks, 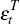 . Although one could proceed by imposing additional
restrictions on the elements of
. Although one could proceed by imposing additional
restrictions on the elements of 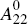 , or using restrictions on any of
, or using restrictions on any of 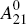 ,
, 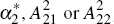 ,[15]
in some applications such restrictions may not be appealing on theoretical
grounds. This is the case, for example, when attempting to distinguish between
fundamental and non-fundamental transitory shocks as considered in the empirical
application below.
,[15]
in some applications such restrictions may not be appealing on theoretical
grounds. This is the case, for example, when attempting to distinguish between
fundamental and non-fundamental transitory shocks as considered in the empirical
application below.
Instead, I assume there exists additional observable information available to the
researcher that allows identification of 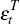 ,
or at least some of the elements in this transitory shock vector. Specifically,
I assume that Equation (15) can be partitioned in a form that is consistent
with the presence of an (r – 1) × 1 vector of fundamental
transitory shocks,
,
or at least some of the elements in this transitory shock vector. Specifically,
I assume that Equation (15) can be partitioned in a form that is consistent
with the presence of an (r – 1) × 1 vector of fundamental
transitory shocks, 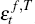 , and a single non-fundamental transitory
shock,
, and a single non-fundamental transitory
shock, 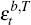 ,[16]
,[16]
I further assume there exists an observable instrument (or set of instruments) 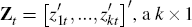 vector (κ ≥ 1), with the properties that,
vector (κ ≥ 1), with the properties that,
That is, there exists one or more instruments for equity prices growth that are correlated
with mispricing shocks, and contemporaneously uncorrelated with either fundamental
transitory or permanent
shocks.[17]
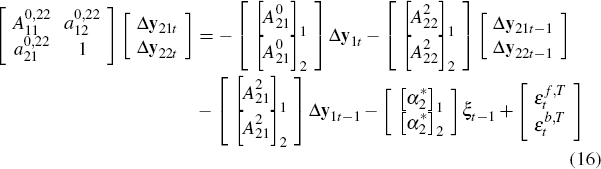
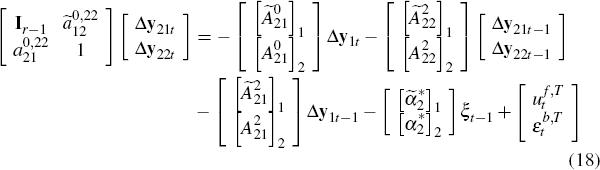
Assuming 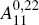 is non-singular, again using a simple premultiplication of Equation (16) yields
is non-singular, again using a simple premultiplication of Equation (16) yields
where
This system can be estimated using a method analogous to that used for the permanent
equations. Specifically, one can estimate the first r – 1 transitory equations using 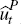 and Zt
as instruments for Δy1t and Δy22t
respectively. The residuals
and Zt
as instruments for Δy1t and Δy22t
respectively. The residuals 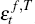 and
and 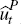 can then be used as
instruments for Δy21t and Δy1t
when estimating the final transitory equation.
can then be used as
instruments for Δy21t and Δy1t
when estimating the final transitory equation.
In sum, this procedure enables identification of the structural mispricing shock,
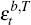 ,
including associated impulse response functions and forecast error variance
decompositions that identify the effects of this shock. If alternative instruments,
or valid restrictions can be imposed to identify the effects of fundamental
transitory shocks, then these too can be used. However, such restrictions are
not required to identity the effects of the mispricing shock.
,
including associated impulse response functions and forecast error variance
decompositions that identify the effects of this shock. If alternative instruments,
or valid restrictions can be imposed to identify the effects of fundamental
transitory shocks, then these too can be used. However, such restrictions are
not required to identity the effects of the mispricing shock.
In the empirical application that follows I eliminate Equation (7) from Equations (6) to (8) and order the vector of observables such that yt = [ct dt nt yt qt pt]′, and so y1t = [ct dt nt yt]′ and y2t = [qt pt]. That is, there are two cointegrating vectors (transitory shocks) in the system (n = 6, r = 2),[18] and I assume that these shocks have direct effects on the quantity and price of equity held by households, and indirect effects on consumption, dividends, non-equity worth and labour income. The latter variables are also those directly perturbed by permanent fundamental shocks.
Footnotes
In taking these approximations, I assume that each variable in the system can be normalised by an appropriate trend (for example, the level of productivity or another variable that captures the long-run growth rate of the economy), and that limit terms associated with iterating these relationships forwards are small (of second-order). I omit linearisation constants and growth rates in unobserved trends in the above approximations. [7]
Note for returns I use the normalisation rt+i Ξ 1n(1+rt+i). [8]
Without loss of generality, I assume when making these substitutions that ρw = ρh. [9]
Note I substitute et out of the system in Equations (6) to (8) in the analysis that follows. [10]
Rather than assuming 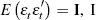 impose normalisation (unity) restrictions on the main diagonal of A0.
[11]
impose normalisation (unity) restrictions on the main diagonal of A0.
[11]
Lütkepohl (2006) provides a review of the regularity conditions under which such an approximation will be valid. [12]
The fact that the number of transitory shocks is equal to the number of cointegrating vectors is an implication of the Granger representation theorem. Lütkepohl (2006) provides a useful review. [13]
This result is derived in Pagan and Pesaran (2008) with respect to Equation (12), and is consistent with the ordering of permanent and transitory shocks. [14]
This is the approach followed by Pagan and Pesaran (2008) after fully identifying the effects of permanent shocks. [15]
I use the notation that 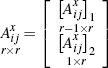 .
A similar partition is used with respect to α*.
[16]
.
A similar partition is used with respect to α*.
[16]
To be clear, only the first two conditions are required for identification. I use
the stronger requirement 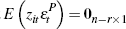 since the proxies for mispricing have desirable properties when used as instruments
in estimating the permanent equations.
[17]
since the proxies for mispricing have desirable properties when used as instruments
in estimating the permanent equations.
[17]
This is confirmed by cointegration matrix rank tests (see Appendix B). [18]