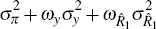RDP 2011-02: Long-term Interest Rates, Risk Premia and Unconventional Monetary Policy 5. Optimal Monetary Policy Rules
April 2011
- Download the Paper 519KB
We assume that the objective of the monetary authority is to minimise a loss function which takes as arguments the variability of inflation, output and the short-term interest rate over the parameters of the policy rule. Formally, the central bank minimises
over the parameters of the policy
rule.[14]
The parameters ωy and 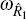 govern the relative
concern for output and short-term interest rate variability. The terms
govern the relative
concern for output and short-term interest rate variability. The terms 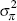 and
and 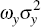 in the loss function are standard. We include the variance of the short-term rate,
in the loss function are standard. We include the variance of the short-term rate,
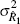 for two reasons. First, as real money balances enter households' utility functions,
the central bank might wish to also attenuate fluctuations of the short-term
rate so as to reduce variations of the opportunity costs of holding money.
Second, as we are exploring the use of instruments of different maturities,
it seems reasonable to penalise instruments which would require additional
volatility of the short rate.
for two reasons. First, as real money balances enter households' utility functions,
the central bank might wish to also attenuate fluctuations of the short-term
rate so as to reduce variations of the opportunity costs of holding money.
Second, as we are exploring the use of instruments of different maturities,
it seems reasonable to penalise instruments which would require additional
volatility of the short rate.
Table 2 evaluates the loss function and its components under a long-term interest
rate rule for 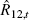 and the Taylor rule for a range of relative weights on output volatility of the
monetary authority. For these preferences,
and the Taylor rule for a range of relative weights on output volatility of the
monetary authority. For these preferences, 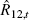 performs slightly better
than the
performs slightly better
than the 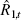 .
For some other preferences, however, long-term interest rate rules of different
maturities do worse, though the differences are also never large. Also note
that the variances of output, inflation and the short rate behave as expected
across the central bank preferences: as the concern for output volatility increases,
the variance of output falls and that of inflation and the short rate
rises.[15]
.
For some other preferences, however, long-term interest rate rules of different
maturities do worse, though the differences are also never large. Also note
that the variances of output, inflation and the short rate behave as expected
across the central bank preferences: as the concern for output volatility increases,
the variance of output falls and that of inflation and the short rate
rises.[15]
Instrument: 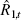 |
Instrument: 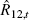 |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| ωy | Loss | 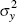 |
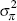 |
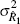 |
Loss | 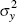 |
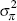 |
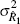 |
|
| 0.20 | 3.54 | 11.77 | 1.15 | 0.75 | 3.48 | 11.60 | 1.12 | 0.72 | |
| 1.00 | 8.54 | 3.80 | 4.62 | 2.52 | 8.49 | 3.83 | 4.54 | 2.48 | |
| 3.00 | 12.49 | 0.99 | 9.22 | 6.26 | 12.47 | 1.03 | 9.08 | 6.05 | |
| Note: All values are multiplied by 10000 | |||||||||
The settings of the optimised rules are similar. Figure 6 shows the loss function as we depart from the optimal value of one of the parameters in the policy rule – holding the other parameters at their optimal values. Thus, borrowing the parameter values from the Taylor rule seems not too costly.
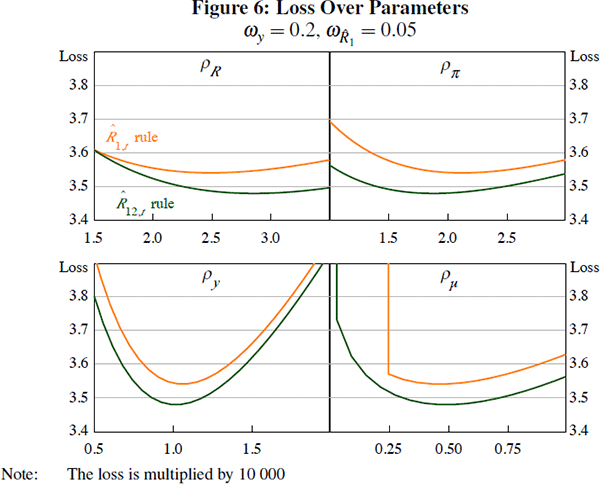
For some preferences long-term interest rate rules perform as well as the Taylor rule, but for some preferences their performance is worse. Overall their performances are quite similar.
Footnotes
This is equivalent to minimising 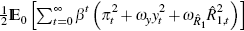 [14]
[14]
When comparing the performance of long-term interest rate rules to each other, a choice must be made regarding the maturity of the frictions. One alternative is to fix the friction at some maturity and then evaluate different long-term interest rate rules. Another alternative is to move the friction with the maturity of the rule. We have done both exercises and found that the performance of long-term interest rates rules is about the same in both cases. [15]