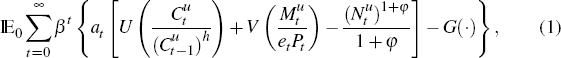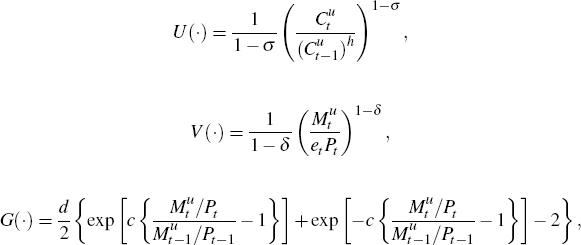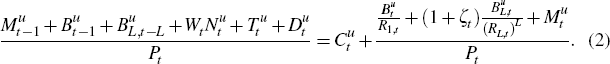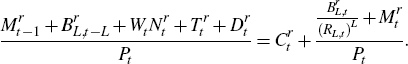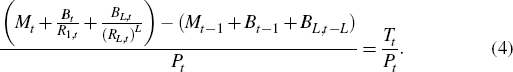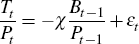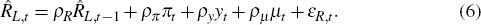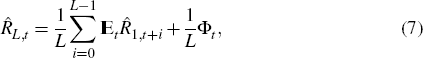RDP 2011-02: Long-term Interest Rates, Risk Premia and Unconventional Monetary Policy 2. Model

In a standard log-linear New Keynesian model, long-term interest rates would be determined solely by the expected path of the short rate. However, in practice, long-term interest rates appear to deviate from the expected path of short-term rates. To take account of this, we are interested in the properties of long-term interest rate rules in a model with an explicit role for an endogenous risk premium, and so use the model developed by Andrés, López-Salido and Nelson (2004) in which there are endogenous deviations from the expectations hypothesis.

Andrés et al (2004) introduce an endogenous risk premium into a standard New Keynesian model by making households differ in their ability to purchase short-term and long-term bonds, together with some other frictions. Unrestricted households can hold both short-term and long-term securities whereas restricted households can only hold long-term securities. While this assumption may be somewhat unrealistic, it is useful in that it produces a tractable model with the realistic property that the risk premium is endogenous. This allows us to explore the simultaneous determination of interest rates and the risk premium when the central bank chooses a rule that sets the price of long-term debt.

The model generates two departures from the expectations hypothesis of the yield curve. First, it adds an exogenous risk premium shock. Second, it incorporates a portfolio balance term that gives a role for money in the yield curve equation. The supply side of the economy is standard, with firms operating in a monopolistically competitive environment and facing price rigidities as in Calvo (1983). For this reason, we do not discuss the supply side further, but discuss, for completeness, the less standard aspects of the model.

Unrestricted households

Unrestricted households make up a proportion, λ, of the population and have preferences over consumption, 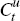, hours worked, 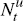, and real money balances, 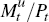; they have habits in consumption and face a cost of adjusting their holdings of real money balances. Their preferences are represented by:

where

and where, e_t is a stationary money demand shock, a_t is a stationary preference shock, β is the discount factor, φ is the inverse of the Frisch labour supply elasticity, σ is the coefficient of relative risk aversion, and δ, c, and d are positive parameters that jointly govern preferences over real money balances.

Each period, unrestricted households enter with money balances, short-term and long-term government debt left over from the previous period, and receive labour income, 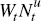, dividends, 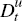, and transfer payments from the government, 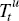. These sources of funds are used to consume, to purchase short-term and long-term government bonds of maturity 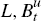and 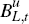, at prices given by 1/R_1,t and 1/R_L,t, and, to hold real money balances to be carried to the next period. Their objective is to choose sequences, 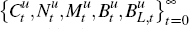, so as to maximise Equation (1) subject to a sequence of period budget constraints of the form:

In addition, short-term and long-term government bonds are imperfect substitutes, that is, both assets are held in positive amounts although their expected yields differ because unrestricted households face two frictions. The first is a stochastic transaction cost in the long-bond market which shifts the price of long-term bonds by 1 + ζ_t, so that households pay (1 + ζ_t)/(R_L,t)^L rather than 1/(R_L,t)^L for one unit of 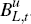. The second captures a liquidity risk in the market for long-term debt. Households which purchase a long-term government bond receive a return from that investment after L periods. Because there are no secondary markets for long-term government bonds in this model, by holding long bonds, households forego liquidity relative to an equivalent holding of short maturity assets. As explained by Andrés et al (2004), agents self-impose a reserve requirement on their long-term investments. Formally, the second friction is a utility cost specified in terms of households' relative holdings of money to long-term government bonds and is given by,

where κ is the inverse of unrestricted agents' steady-state money-to-long-term debt ratio and ν > 0 is a parameter that governs the magnitude of the cost.

Restricted households

Restricted households can hold long-term government bonds but not short-term government bonds. Their preferences are like those of Equation (1), but their period budget constraint takes the form:

Restricted agents do not face the other frictions. As explained by Andrés et al (2004), this assumption may be relaxed to a large extent, to obtain endogenous deviations from the expectations hypothesis that matter for aggregate demand. For this to be the case, agents must have different attitudes towards risk; restricted agents must regard long-term debt as a less risky investment than unrestricted agents. In any case, the assumption that a fraction of the population are not concerned about the price-risk of long-term debt can be motivated by appealing to those agents, like pension funds, that intend to hold the long-term debt to maturity.

Government

The government does not spend and transfers all revenues to households. It finances these transfers through seigniorage and through the issuance of long-term and short-term government bonds. The government period budget constraint is:

The supply of long-term government bonds follows an exogenous stationary process; the supply of short-term government bonds is sufficient to make up the short fall in government financing, after seigniorage and long-term bond issuance; and transfers are set according to the fiscal rule:

where χ Є (0,1).

Monetary policy

We close the model in one of two ways. In one case, we assume that the central bank follows a policy rule in which it sets the short rate. This takes the form:

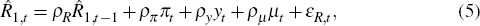
where 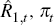and y_t are the log deviations of the short rate, inflation and output from their steady-state values, ε_R,t is a stationary monetary policy shock, and µ_t is the growth of the money supply. Alternatively, we assume instead that the central bank sets the long-term interest rate according to a policy rule of the form:

Long-term interest rates

One can show that the nominal interest rate in period t associated with a zero-coupon bond that promises to pay one dollar at the end of period t + L – 1 is determined by:

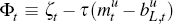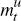where , with and 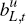the log deviations of real money balances and long-term debt holdings from their steady-state values, and τ > 0 is a function of the structural parameters, in particular of the parameters that determine the magnitude of the financial frictions. Two terms govern the determination of 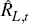. The first, 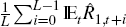, is the expectations hypothesis term, whereby the expected path of the short rate impacts on the long rate; if there were an increase in agents' expectations of future short-term rates, to avoid arbitrage opportunities, the long-rate must rise. The second is the risk premium, 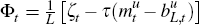which embodies the two frictions that we discussed above: ζ_t is the exogenous component of risk premium and 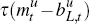is the endogenous one which depends on the relative stocks of the liquid and illiquid assets. 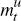If, for example, falls, the loss of liquidity implies that the long-term interest rate must rise to induce agents to hold long-term bonds. In what follows, the parameters are set to the values estimated by Andrés et al (2004). These are summarised in Table B1.^[5]

Footnote

The results are robust to a wide range of parameter values. The MATLAB files are available on request. [5]