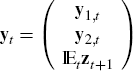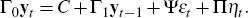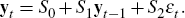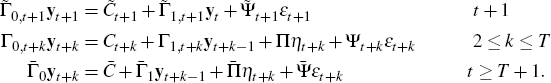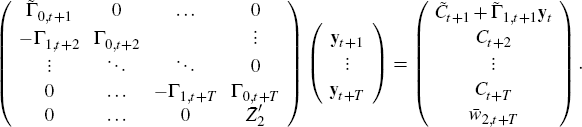RDP 2011-02: Long-term Interest Rates, Risk Premia and Unconventional Monetary Policy Appendix C: Anticipated Structural Changes Under Rational Expectations

Appendix C: Anticipated Structural Changes Under Rational Expectations

Following Cagliarini and Kulish (2008), write the model in matrix form as follows

where the state vector is defined by

and where y_1,t is an (n₁ × 1) vector of exogenous and some endogenous variables, and y_2,t is an (n₂ × 1) vector with those endogenous variables for which conditional expectations appear, z_t+1, (k × 1), contains leads of y_2,t; in the model above, however, z_t+1 = y_2,t+1 and k = n₂. The dimension of y_t is n × 1, where n = n₁ + n₂ + k. 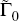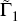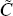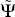Also, we assume ε_t to be an l ×1 vector of serially uncorrelated processes, and are (n₁ + n₂) × n matrices, is (n₁ + n₂) × 1 and is (n₁ + n₂) × l.

η_t is the vector of expectations revisions given by,

where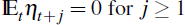

Augment the system defined by Equation (C1) with the k equations from Equation (C2) to obtain Equation (8) reproduced below

A unique rational expectations solution takes the form:

Consider that at the beginning of forecast horizon, the monetary authority announces how the policy parameters will vary in the future. An announcement of this form entails a form of structural change, from the perspective of the standard solution for rational expectations models. This induces a sequence of structures of the form, 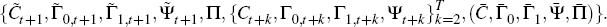Therefore, the system evolves as follows

Under regularity conditions the solution for y_t+1,...,y_t+T satisfies

After t + T, the standard solution for 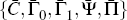applies.