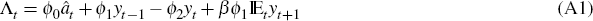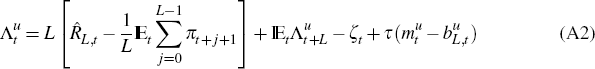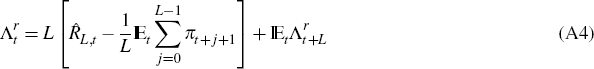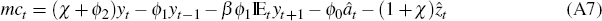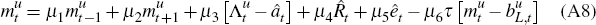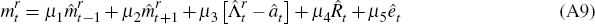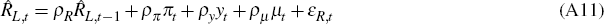RDP 2011-02: Long-term Interest Rates, Risk Premia and Unconventional Monetary Policy Appendix A: The Linearised Equations

The full set of linearised equations is given by:

All variables are in log deviations from steady state. Equation (A1) gives the evolution of the aggregate marginal utility of wealth, Λ_t, linking it to the preference shock â_t and output y_t. Equations (A2) to (A4) give the restricted and unrestricted agents' intertemporal relationships. Equation (A2) is the unrestricted agents' first-order condition for long-term debt accumulation, where 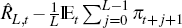is the long-term real interest rate, 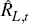is the nominal long-term interest rate and π_t is inflation, and 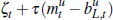is the risk premium, where ζ_t is the exogenous component of the premia, m_t is money demand and b_L,t long-term real bond holdings. Equation (A4) gives the restricted agents' first-order condition for long-term debt accumulation. Equation (A5) combines the restricted and unrestricted agents' Lagrange multipliers, weighted by λ, the proportion of unrestricted agents. Equations (A6) and (A7) give the supply-side relations, linking inflation to marginal costs mc_t and technology shocks . 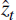Equations (A8) to (A10) govern money demand relationships, where ê_t is a money demand shock. Equation (A10) aggregates across agents' money holdings. Equation (A11) gives the Taylor-type rule for a central bank targeting interest rates of maturity L with money growth µ_t specified by Equation (A12). Equation (A13) aggregates across agents' long-term bond holdings. The exogenous processes are given by Equations (A14) to (A19).