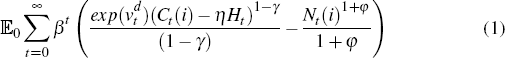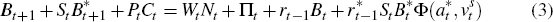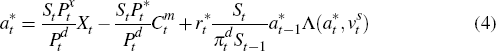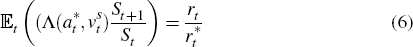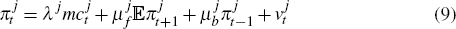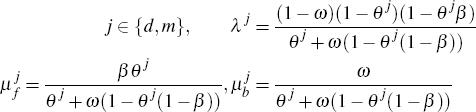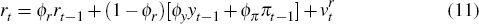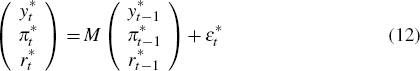RDP 2010-02: Learning in an Estimated Small Open Economy Model 2. A Small Open Economy DSGE Model
March 2010
- Download the Paper 280KB
This section sketches the building blocks of the small open economy dynamic stochastic general equilibrium (DSGE) model that we estimate. The model closely follows Justiniano and Preston (2010) and Nimark (2007). The log-linearised equations are given in Appendix A.[4]
2.1 Households
The economy consists of a continuum of identical households who maximize their lifetime utility over consumption and leisure. Each household i has the following preference for lifetime utility:
where: β is the household's rate of time preference; Ct
is the time t consumption bundle consisting of both domestically produced
and imported consumption goods; Ht = Ct−1
captures external habit formation; Nt is hours of labour
supplied; γ is the inverse elasticity of intertemporal substitution;
φ is the inverse elasticity of labour supply; η is
the degree of habit formation; and 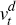 is an exogenous consumption
preference shock that follows the AR(1) process
is an exogenous consumption
preference shock that follows the AR(1) process
Households are constrained by the following nominal budget constraint:
where expenditures appear on the left-hand side and sources of income on the right-hand
side. Households work in a perfectly competitive labour market and earn a nominal
wage (Wt) for every hour (Nt) of labour supplied.
As owners of monopolistic firms, they also receive profits (Πt).
Households allocate their income each period between domestic bonds (Bt+1),
foreign bonds 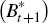 and consumption goods Ct (Pt denotes the
CPI price
index);[5]
St is the nominal exchange rate defined such that an increase
in St implies a depreciation of the domestic currency.
For domestic bonds and foreign bonds the nominal yields are rt
and
and consumption goods Ct (Pt denotes the
CPI price
index);[5]
St is the nominal exchange rate defined such that an increase
in St implies a depreciation of the domestic currency.
For domestic bonds and foreign bonds the nominal yields are rt
and 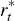 ,
respectively. There is a premium
,
respectively. There is a premium 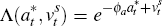 associated with having a net foreign position,
which is a function of the real net holding of foreign bonds
associated with having a net foreign position,
which is a function of the real net holding of foreign bonds 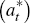 and a risk premium shock
and a risk premium shock 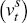 .
This is necessary to ensure a well-defined steady state (Benigno
2009).[6] The evolution
of net foreign assets
.
This is necessary to ensure a well-defined steady state (Benigno
2009).[6] The evolution
of net foreign assets 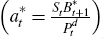 at the aggregate level satisfies the following
equation (where we have assumed a zero net supply of domestic bonds):
at the aggregate level satisfies the following
equation (where we have assumed a zero net supply of domestic bonds):
The risk premium shock follows the AR(1) process
Arbitrage implies that the expected marginal utility from domestic bonds must match that of foreign bonds, which leads to the uncovered interest rate parity condition, adjusted for the foreign bond premium:
2.2 Firms
There are two types of firms: producers and importers. Producers manufacture a single differentiated good in a monopolistically competitive market. This good can be sold to the producers' domestic market or to importers in the foreign economy. Domestic exporters sell the final domestic good at price Px = Pd/S so there is complete exchange rate pass-through in the export market. Output of production firms is given by:
where: Yt is the quantity of the domestic good produced; Nt
is hours of labour; and 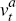 is a productivity shock that follows the
AR(1) process
is a productivity shock that follows the
AR(1) process
Domestic importers purchase the foreign variety of the good and resell it in the domestic market. The import market is competitive and thus importers are unable to influence the price that they pay. However, they are assumed to have pricing power when selling to the domestic market.
We introduce price rigidities suggested by Galí and Gertler (1999) to capture the observed inertia in domestic and imported consumption good inflation. Each period, only a fraction of firms are able to change their price (a fraction θd of firms producing domestically and a fraction θm of importing firms do not change prices in a given period). A fraction ω of the domestic producers and importers that do change prices use a rule-of-thumb that links their price to lagged inflation (in their own sector). The rest (1 − ω) set their prices optimally. The log-linearised new Keynesian Phillips curves for domestic goods and imports are
where: j refers to domestic (d) or imported (m) good sectors;
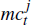 is the marginal cost of production; and
is the marginal cost of production; and 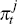 is inflation. There is a cost-push
shock
is inflation. There is a cost-push
shock 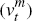 in the import Phillips curve (but not in the domestic Phillips curve), which follows
an AR(1) process of
in the import Phillips curve (but not in the domestic Phillips curve), which follows
an AR(1) process of
2.3 Monetary Policy
The nominal interest rate (rt) is set according to a Taylor rule based on lagged interest rates and time t−1 information on inflation and output:
where: all variables are expressed as logarithmic deviations from the steady state;
yt is the domestic output gap; πt
is CPI inflation; and 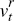 is an exogenous monetary policy shock.
is an exogenous monetary policy shock.
McCallum (1999) argues that rules with this feature fit the data better because the informational assumptions are more realistic. Bullard and Mitra (2002) show that under learning this particular form of the Taylor rule has superior stability properties for a wide variety of parameter combinations.
2.4 The World Economy
The foreign economy (the rest of the world) is a large economy. We represent the foreign economy as an unrestricted VAR(1) of output, inflation and the nominal interest rate:
where 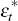 is the world shock vector and
is the world shock vector and 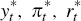 are respectively foreign output (linearly
detrended), inflation and the nominal interest rate expressed as percentage
deviations from their sample means. The foreign economy is treated as exogenous
to the domestic economy and thus the coefficient matrix M is estimated
separately from the rest of the model.
are respectively foreign output (linearly
detrended), inflation and the nominal interest rate expressed as percentage
deviations from their sample means. The foreign economy is treated as exogenous
to the domestic economy and thus the coefficient matrix M is estimated
separately from the rest of the model.
Footnotes
A step-by-step derivation is available from the authors on request. [4]
The consumption bundle Ct is a standard constant elasticity of substitution
(CES) aggregated index of domestically produced and imported bundles 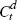 and
and 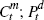 and
and 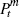 refer to the price indices of these bundles.
[5]
refer to the price indices of these bundles.
[5]
If the domestic economy is a net borrower, households are charged a premium on the foreign interest rate. On the flip side, net lender economies receive a premium on the foreign interest rate. [6]