RDP 2010-02: Learning in an Estimated Small Open Economy Model 4. Results
March 2010
- Download the Paper 280KB
4.1 Parameter Estimates
We first estimate the model described in Equations (A1)–(A16) for the 1993–2007 sample under the assumption of rational expectations. The estimates of the rational expectations parameters are used as starting values when estimating the learning model, which is based on the same prior information as used for the rational expectations model.[11] We then compare the results from the learning model to those from the rational expectations model.
4.1.1 Rational expectations
Table 1 presents the estimation results for the rational expectations model. A number of these are worth noting. The degree of habit formation in consumption (η) is much stronger than the 0.33 reported in Justiniano and Preston (2010). The rule-of-thumb parameter (ω) implies that both domestic and imported inflation are highly persistent processes. The estimated coefficients for the interest rate rule are broadly similar to those reported in other studies using Australian data (Jääskelä and Nimark 2008; Nimark 2007; and Kulish and Rees 2008). The persistence of the AR(1) processes are much lower in our model compared to Justiniano and Preston (2010) but higher or the same as in Nimark (2007). The most persistent estimated shock process is the risk premium shock (ρs). The upper bound of the 90 per cent confidence interval for this parameter exceeds 0.95; however the posterior distribution is rather wide, indicating substantial parameter uncertainty.
| Parameters | Prior | Posterior | ||||||
|---|---|---|---|---|---|---|---|---|
| Distribution | Mean | Std dev | Mean | Std dev | 5% | 95% | ||
| Households and firms | ||||||||
| α | 0.18 | 0.18 | ||||||
| β | 0.99 | 0.99 | ||||||
| γ | Gamma | 1.20 | 0.20 | 1.221 | 0.198 | 0.913 | 1.566 | |
| η | Uniform | [0,1) | 0.870 | 0.050 | 0.774 | 0.939 | ||
| φ | Gamma | 2.00 | 0.40 | 1.604 | 0.325 | 1.116 | 2.176 | |
| ω | Beta | 0.20 | 0.05 | 0.267 | 0.063 | 0.167 | 0.373 | |
| δ | Gamma | 1.50 | 0.10 | 1.510 | 0.098 | 1.351 | 1.674 | |
| δx | Gamma | 1.50 | 0.10 | 1.497 | 0.099 | 1.339 | 1.662 | |
| θd | Beta | 0.60 | 0.05 | 0.832 | 0.025 | 0.788 | 0.870 | |
| θm | Beta | 0.60 | 0.05 | 0.609 | 0.048 | 0.528 | 0.687 | |
| ϕa | Gamma | 0.10 | 0.05 | 0.117 | 0.065 | 0.043 | 0.242 | |
| Taylor rule | ||||||||
| ρr | Beta | 0.75 | 0.01 | 0.741 | 0.010 | 0.725 | 0.758 | |
| ϕπ | Gamma | 1.50 | 0.10 | 1.556 | 0.010 | 1.395 | 1.725 | |
| ϕy | Gamma | 0.20 | 0.10 | 0.199 | 0.077 | 0.089 | 0.340 | |
| Persistence of shocks | ||||||||
| ρa | Beta | 0.60 | 0.20 | 0.585 | 0.061 | 0.481 | 0.682 | |
| ρs | Beta | 0.60 | 0.20 | 0.625 | 0.308 | 0.172 | 0.978 | |
| ρd | Beta | 0.60 | 0.20 | 0.678 | 0.084 | 0.531 | 0.806 | |
| ρm | Beta | 0.60 | 0.20 | 0.111 | 0.050 | 0.039 | 0.200 | |
| Std dev of shocks (×10−2) | ||||||||
| σa | Inv gamma | 0.1 | 2 | 0.097 | 0.040 | 0.054 | 0.175 | |
| σs | Inv gamma | 0.1 | 2 | 0.109 | 0.063 | 0.052 | 0.227 | |
| σd | Inv gamma | 0.1 | 2 | 0.290 | 0.220 | 0.101 | 0.707 | |
| σm | Inv gamma | 0.1 | 2 | 0.127 | 0.083 | 0.060 | 0.265 | |
| σr | Inv gamma | 0.1 | 2 | 0.034 | 0.005 | 0.027 | 0.042 | |
| Notes: The posterior statistics are based on 2 million draws using the Markov Chains Monte Carlo (MCMC) method with a 25 per cent burn-in period. For the inverse gamma prior distributions, the mode and the degrees of freedom are reported. Measurement errors (et in Equation (19)) are estimated assuming no prior information and are not shown here. The marginal likelihood is −1,554. | ||||||||
4.1.2 Constant-gain least squares learning
The estimation results for the model with learning are presented in Table 2. In short, our results show that learning is not a substitute for the structural sources of persistence and habit formation in consumption. A comparison of the estimates of the parameters for mechanical persistence (η – habits; ω – the share of the rule-of-thumb producers) shows a noticeable increase in both compared with the rational expectations model estimates.
| Parameters | Prior | Posterior | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Distribution | Mean | Std dev | Mean (RE) |
Mean | Std dev | 5% | 95% | ||
| Households and firms | |||||||||
| α | 0.18 | 0.18 | 0.18 | ||||||
| β | 0.99 | 0.99 | 0.99 | ||||||
| γ | Gamma | 1.20 | 0.20 | 1.221 | 1.284 | 0.074 | 1.152 | 1.399 | |
| η | Uniform | [0,1) | 0.870 | 0.973 | 0.006 | 0.962 | 0.982 | ||
| φ | Gamma | 2.00 | 0.40 | 1.604 | 1.045 | 0.126 | 0.814 | 1.257 | |
| ω | Beta | 0.20 | 0.05 | 0.267 | 0.370 | 0.047 | 0.294 | 0.456 | |
| δ | Gamma | 1.50 | 0.10 | 1.510 | 1.498 | 0.059 | 1.396 | 1.601 | |
| δx | Gamma | 1.50 | 0.10 | 1.497 | 1.504 | 0.066 | 1.396 | 1.628 | |
| θd | Beta | 0.60 | 0.05 | 0.832 | 0.733 | 0.029 | 0.685 | 0.780 | |
| θm | Beta | 0.60 | 0.05 | 0.609 | 0.653 | 0.032 | 0.595 | 0.703 | |
| ϕa | Gamma | 0.10 | 0.05 | 0.117 | 0.242 | 0.051 | 0.181 | 0.344 | |
| ḡ | Uniform | [0,1) | 0.0002 | 0.0001 | 0.0001 | 0.0003 | |||
| Taylor rule | |||||||||
| ρr | Beta | 0.75 | 0.01 | 0.741 | 0.751 | 0.009 | 0.736 | 0.765 | |
| ϕπ | Gamma | 1.50 | 0.10 | 1.556 | 1.493 | 0.060 | 1.377 | 1.581 | |
| ϕy | Gamma | 0.20 | 0.10 | 0.199 | 0.153 | 0.062 | 0.069 | 0.279 | |
| Persistence of shocks | |||||||||
| ρa | Beta | 0.60 | 0.20 | 0.585 | 0.878 | 0.043 | 0.801 | 0.944 | |
| ρs | Beta | 0.60 | 0.20 | 0.625 | 0.360 | 0.140 | 0.213 | 0.714 | |
| ρd | Beta | 0.60 | 0.20 | 0.678 | 0.789 | 0.113 | 0.552 | 0.894 | |
| ρm | Beta | 0.60 | 0.20 | 0.111 | 0.510 | 0.085 | 0.366 | 0.676 | |
| Std dev of shocks (×10−2) | |||||||||
| σa | Inv gamma | 0.1 | 2 | 0.097 | 0.076 | 0.021 | 0.049 | 0.116 | |
| σs | Inv gamma | 0.1 | 2 | 0.109 | 0.102 | 0.043 | 0.057 | 0.180 | |
| σd | Inv gamma | 0.1 | 2 | 0.290 | 0.107 | 0.040 | 0.061 | 0.181 | |
| σm | Inv gamma | 0.1 | 2 | 0.127 | 0.071 | 0.017 | 0.048 | 0.102 | |
| σr | Inv gamma | 0.1 | 2 | 0.034 | 0.033 | 0.005 | 0.027 | 0.042 | |
| Notes: The posterior statistics are based on 2 million draws using the Markov Chains Monte Carlo (MCMC) method with a 25 per cent burn-in period. For the inverse gamma prior distributions, the mode and the degrees of freedom are reported. Measurement errors (et in Equation (19)) are estimated assuming no prior information and are not shown here. The marginal likelihood is −1,840. | |||||||||
Indeed, this can be seen in Table 3, which compares the implied reduced-form Phillips curve coefficients (see Equation (9)) based on the (mean) rational expectations and learning parameter estimates. The forward-looking components are more prominent than the backward-looking components, though this is more so under rational expectations than under learning.
| Parameter | Rational expectations | Learning |
|---|---|---|
| Domestic goods | ||
| λd : slope of the Phillips curve | 0.020 | 0.042 |
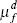 : inflation – forward : inflation – forward |
0.751 | 0.660 |
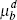 : inflation – backward : inflation – backward |
0.243 | 0.336 |
| Imported goods | ||
| λm | 0.130 | 0.076 |
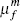 |
0.690 | 0.633 |
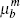 |
0.306 | 0.363 |
These findings are in contrast with Milani (2007), who finds that the parameters for structural sources of persistence uniformly decrease when learning is introduced to the model. However, our results are consistent with estimates based on larger DSGE models such as in Murray (2008) and Slobodyan and Wouters (2009). They find that learning either increases the parameter estimates on mechanical persistence or does not affect them.
We find that learning changes the degree of persistence of the shocks, in some cases quite substantially. However, the direction of these changes is not uniform. The persistence of the productivity (ρa), preference (ρd) and the cost-push (ρm) shocks increase while the persistence of the risk premium shock (ρs) decreases. The increase in the parameter related to net foreign assets (ϕa) suggests that learning cannot be used to replace the high amount of persistence required in the UIP condition to model the real exchange rate effectively. Milani (2007) and Murray (2008) both find that the estimates of the persistence of shocks are quite different under learning; some are larger and some are smaller. Slobodyan and Wouters (2009) find that most estimated persistence parameters remain unchanged or fall.
We find that the standard deviation of the shocks is smaller or the same under learning. However, Milani (2007) and Murray (2008) find that they are broadly similar or increase while Slobodyan and Wouters (2009) find the majority are similar but those that change do not do so in a consistent way.
A comparison of the 90 per cent confidence intervals shows that uncertainty regarding most parameter estimates is lower under learning than under rational expectations. Only, the estimates of the persistence of the cost-push shock (ρm) and consumption preference shock (ρd) are less precise.
4.2 The Transmission and Propagation of Shocks
To gauge the role of learning in transmitting different types of shocks we examine the impulse responses of macroeconomic variables in the model.
4.2.1 Monetary policy shock
Impulse responses for key variables to an unexpected 100 basis point tightening of monetary policy are shown in Figure 1. In both the rational expectations model and the learning model the shock leads to a fall in output, inflation and consumption and an appreciation of the real exchange rate. The shape of the responses in the learning model are similar to the rational expectations model but generally show more persistence and inertia. One particularly interesting response is that of the real exchange rate. While the peak effect occurs in the first quarter in both cases, under learning the effect is much more prolonged. This is consistent with empirical evidence provided in data-driven SVAR models (see Liu (2008) for Australia, and Eichenbaum and Evans (1995) and Faust and Rogers (2003) for the United States). Although our parameter estimates indicate that learning does not preclude the need to add a risk premium to the ‘pure’ UIP condition, the impulse responses suggest that it enhances the dynamics of the model in propagating policy shocks. All of the impulse response functions show that the peak occurs later and that it takes longer for the shock to completely propagate through the system under learning than under rational expectations. The magnitudes of the real exchange rate, consumption and GDP responses are more subdued in the learning model relative to the rational expectations model. This is confirmed by the parameter estimates, which suggest that consumption decisions are less responsive to the expected real interest rate under learning.[12] However, the CPI responds by more, which is partly due to increased structural inflation persistence (a larger rule-of-thumb parameter, ω) that makes inflation more sensitive to movements in the marginal cost (the sensitivity of CPI inflation is a weighted average of λd and λm; see Equation (A9)).
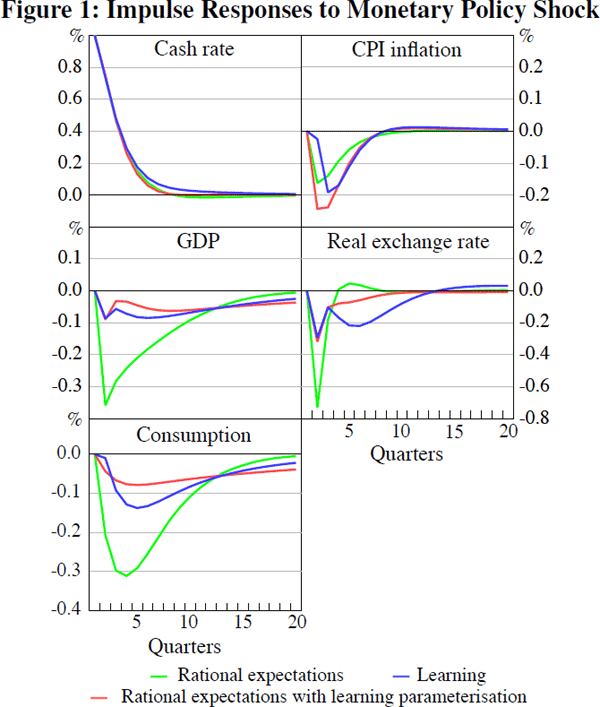
It may be that the change in the dynamic response is due to the fact that the parameters of mechanical sources of persistence are higher in the learning model, rather than because of learning per se. To demonstrate that the change in dynamics is, at least in part, due to the learning process, we plot the impulse response functions for an economy where expectations are rational but use the estimated structural parameters implied by the learning model (given in Table 2). For the real exchange rate and GDP it is clear that the changed shape of the impulse response can be attributed to learning. In the absence of learning, this parameterisation (shown in red) generally results in much smaller responses but, more importantly, with a similar shape as under the estimated rational expectations model (shown in green). Hence the learning mechanism is leading to more persistence in the economy. In the learning model, all the forward-looking variables (consumption, inflation and the exchange rate) are more persistent. As a result, the cash rate response also returns more slowly to baseline. It is worth noting that the majority of the reduction in the size of the response between the rational expectations and the learning models can be attributed to the change in the parameters. Learning actually amplifies the fluctuations: the magnitude of the responses in the rational expectations model with learning parameterisation is more subdued than under learning. From this exercise we conclude that learning, by itself, changes the propagation of the monetary policy shock, extending the response of the exchange rate, output and consumption, in addition to delaying the response of inflation and consumption.
4.2.2 Productivity shock
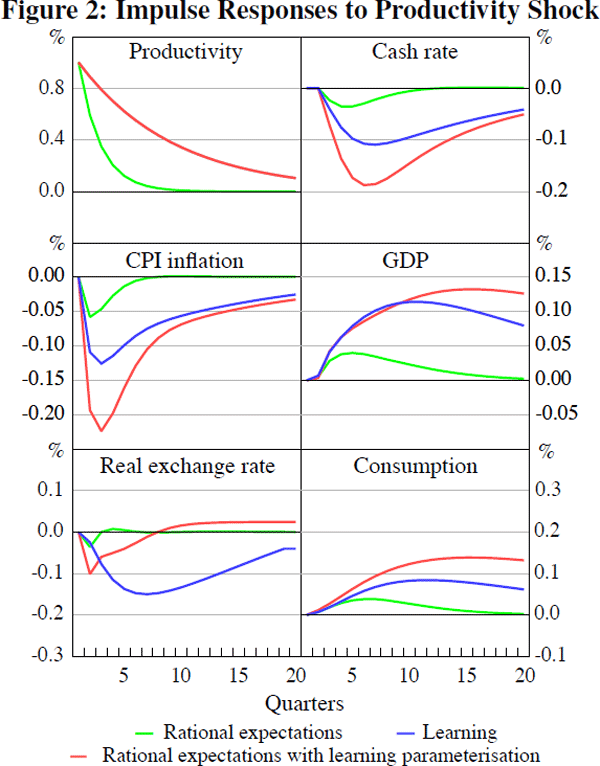
Figure 2 shows impulse responses of key variables to a one standard deviation productivity shock. It is necessary to emphasise at the outset that the shock is much more persistent in the learning model, which creates an additional consideration when comparing impulse response functions. The difference in the decay of the shock is shown in the top-left panel in Figure 2. As expected, the increase in productivity increases GDP and consumption. Inflation falls, and the cash rate is lowered; the real exchange rate appreciates. Once again, learning results in a more protracted and persistent response in the real exchange rate, suggesting that learning may slow down the adjustment to the productivity shock. We repeat the exercise conducted in the previous section and use the learning parameterisation in the rational expectations model; these impulse response functions will, among other things, include the effect of the increase in the persistence of the productivity shock. As before, the real exchange rate response is more persistent and pronounced under learning. Due to the larger appreciation of the exchange rate, and more modest decline in the cash rate, the responses of output, consumption and inflation are more subdued and short-lived under learning.
4.3 Robustness: Looser Priors
To generate plausible dynamics in the rational expectations model several parameters (ω, θd, θm and ρr) require tight priors. As a robustness check, we re-estimate both the rational expectations and learning models with a set of looser priors on the rule-of-thumb (ω), Calvo (θd, θm) and interest rate smoothing (ρr) parameters. For the first three, the standard deviation is doubled from 0.05 to 0.1, and for the fourth it is increased from 0.01 to 0.05. The results for the re-estimated rational expectations model are detailed in Table C1 in Appendix C. There are several noticeable changes in the parameter estimates. With these looser priors, the estimate of a proportion of the rule-of-thumb firms (ω) has risen from 0.27 to 0.89 and the uncertainty in the estimate of this parameter has tripled. The persistence of the interest rate (ρr) falls from 0.74 to 0.66.[13] The paths of the impulse response functions also move and the confidence intervals are wider.
Table 4 summarises the reduced-form Phillips curve coefficients in the rational expectations and learning models under these looser priors. In contrast to the earlier baseline results (Table 3), in the learning model the Phillips curves are less backward-looking.
| Parameter | Rational expectations | Learning |
|---|---|---|
| Domestic goods | ||
| λd : slope of the Phillips curve | 0.007 | 0.011 |
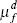 : inflation – forward : inflation – forward |
0.434 | 0.805 |
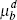 : inflation – backward : inflation – backward |
0.566 | 0.189 |
| Imported goods | ||
| λm | 0.002 | 1.056 |
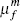 |
0.473 | 0.530 |
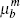 |
0.526 | 0.465 |
The difference in the propagation of shocks between the ‘tight’ and ‘loose’ prior specifications for the rational expectations and learning models is also interesting. Table 5 shows the difference between the cumulative median impulse response for the two prior sets. This is reported as the sum of the absolute value of the difference in the response at each quarter for the first 20 quarters. For the monetary policy shock the difference between the prior specifications is lower under learning than under rational expectations for three of the five impulse responses. However, for the productivity shock the difference between the prior specifications is always larger under learning than it is under rational expectations. Table 5 also shows the sum of the absolute differences in the width of the 90 per cent confidence intervals for each period. Again, the change in the width of the confidence intervals between the prior choices is mostly smaller for the monetary policy shock under learning, while for the productivity shock it is always larger under learning than it is under rational expectations.
| Variable | Median(a) | Confidence interval width(b) | |||
|---|---|---|---|---|---|
| Rational expectations | Learning | Rational expectations | Learning | ||
| Monetary policy shock | |||||
| Cash rate | 0.29 | 0.40 | 1.41 | 1.80 | |
| CPI inflation | 0.48 | 0.37 | 0.76 | 0.12 | |
| Output | 0.76 | 0.40 | 1.23 | 0.80 | |
| Consumption | 0.65 | 0.23 | 1.38 | 0.88 | |
| Real exchange rate | 1.30 | 1.50 | 2.40 | 1.83 | |
| Productivity shock | |||||
| Cash rate | 0.22 | 1.05 | 0.48 | 0.85 | |
| CPI inflation | 0.25 | 0.91 | 0.51 | 0.90 | |
| Output | 0.44 | 1.35 | 1.02 | 1.18 | |
| Consumption | 0.32 | 0.86 | 0.95 | 0.43 | |
| Real exchange rate | 0.68 | 3.73 | 1.65 | 2.09 | |
Notes: (a) The sum of the absolute value of the differences between the
tight prior and looser prior impulse response functions at each period.
Only the first 20 quarters are considered. Calculated as 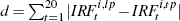 , where , where 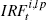 denotes the response of
variable i at time t under ‘loose’ prior,
and denotes the response of
variable i at time t under ‘loose’ prior,
and 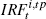 denotes the same metric under the ‘tight’ prior. (b) The sum of the
absolute value of the difference between the width of the confidence interval
at each period. Calculated as denotes the same metric under the ‘tight’ prior. (b) The sum of the
absolute value of the difference between the width of the confidence interval
at each period. Calculated as 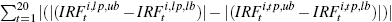 , where ub (lb)
denotes the upper (lower) bound. , where ub (lb)
denotes the upper (lower) bound. |
|||||
Overall, then, the evidence is mixed as to whether the priors do more or less work under learning than they do under rational expectations. However, comparing the fit of the rational expectations and learning models (carried out using Geweke's (1999) Modified Harmonic Mean measure of the marginal likelihood) suggests that data marginally prefer the learning model in the case of the looser set of priors.
4.4 Robustness: MSV Learning
In this section we summarise the estimation results assuming MSV learning. That is, we endow the agents with the reduced-form specification that they would use under the rational expectations equilibrium when forming expectations about future variables.
Tables C3 and C4 provide the parameter estimates under MSV learning assuming the two different prior specifications as before. (These should be compared with Tables 1 and C1, respectively.) A quick glance at these parameter estimates shows that the learning model relies at least as much as the rational expectations model on the mechanical sources of persistence. Habit formation is stronger and most of the shock processes are more persistent under learning. But whether or not inflation is more persistent under learning is unclear; in the ‘loose’ prior specification (Table C4) the reduced-form coefficients of the Phillips curves for both domestic and imported goods imply more forward-looking behaviour under learning, but with the ‘tight’ prior (Table C3) this is less clear-cut. Figures C1 and C2 plot impulse responses to monetary and productivity shocks. Even though the MSV learning rule does not contain a lagged exchange rate term, the real exchange rate does not peak immediately after the productivity shock. With regard to the monetary policy shock, it appears that the tighter prior slows down the adjustment of the exchange rate; under the looser prior with MSV learning the exchange rate behaves more in line with that of the rational expectations model (Figure 1).
To sum up the results of Section 4, it seems that mechanical sources of persistence are needed to match the inertial behaviour in data, however there is some evidence that the data prefer the learning model in the case of looser priors.
Footnotes
The initial value of Φt (Φ0), in Equation (16) is computed using the structural presentation given in Equation (13) at the estimated rational expectations parameter values. The initial value of Rt (R0) is the variance from the data series generated by the Kalman filter. [11]
From Equation (A13) the relevant coefficient is 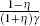 ,
the mean of which is 0.012 under learning compared with 0.057 under rational
expectations.
[12]
,
the mean of which is 0.012 under learning compared with 0.057 under rational
expectations.
[12]
The learning model is also estimated under the looser prior specifications (using the same starting values as before). The results are detailed in Table C2. ω, a proportion of the rule-of-thumb firms is lower, but the habit formation parameter (η) stays high, and is higher than in rational expectations version of the model. [13]