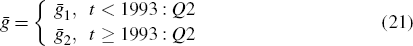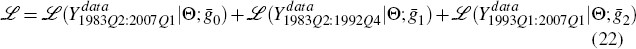RDP 2010-02: Learning in an Estimated Small Open Economy Model 5. Longer Sample: Break in the Gain Parameter
March 2010
- Download the Paper 280KB
It can be argued that the gain parameter varies over time and is lower in periods of macroeconomic stability. This makes sense because a higher gain parameter means that the past is discounted faster; if there is less stability, the recent past is more informative than the more distant past. It is therefore plausible that more credible monetary regimes, with lower and less volatile inflation, should be associated with a lower gain parameter. Accordingly, we look for a break in the gain parameter in 1993, when the Reserve Bank of Australia adopted the current inflation-targeting framework. To do this, we re-estimate the learning model from 1984 (the floating of the Australian dollar) onwards. The learning process is initialised using the rational expectations parameterisation estimated over the longer sample, and all the parameters of the learning model are estimated. ḡLS, the gain parameter for this longer sample (without allowing for the regime shift), is 0.0013, much higher than the gain parameter ḡIT for the shorter post-inflation-targeting sample, which is 0.0002 (Tables 2 and 6). While this is consistent with a shift to a more credible regime, the long sample incorporates the regime shift, which by itself could push up the gain parameter.
| Parameters | Prior | Posterior | ||||
|---|---|---|---|---|---|---|
| Distribution | Mode | Std dev | 5% | 95% | ||
| Baseline: Inflation-targeting period, no break | ||||||
| ḡIT | Uniform [0,1) | 0.0002 | 0.0001 | 0.0001 | 0.0003 | |
| Long sample, no break | ||||||
| ḡLS | Uniform [0,1) | 0.0013 | 0.0011 | 0.0001 | 0.0031 | |
| Break model | ||||||
| ḡ1 | Uniform [0,1) | 0.0004 | 0.0001 | 0.0002 | 0.0006 | |
| ḡ2 | Uniform [0,1) | 0.0003 | 0.0003 | 0.0001 | 0.0010 | |
| Notes: The posterior statistics are based on 2 million draws using the Markov Chains Monte Carlo (MCMC) method with a 25 per cent burn-in period. For the inverse gamma prior distributions, the mode and the degrees of freedom are reported. Measurement errors (et in Equation (19)) are estimated assuming no prior information and are not shown here. All parameters described in Table 2 were estimated jointly with the gain parameters using the prior information described in Table 2. | ||||||
To deal with this we examine the evidence of the effect of the regime shift on learning by allowing the gain parameter to break at the time of the adoption of the inflation target. That is:
The likelihood of this ‘break’ model is given as the sum of the likelihood of the whole sample and the two sub-samples
where Θ denotes a vector of all the other model parameters, which are assumed to be sample-invariant. (This is why the whole sample component appears in the likelihood function.)[14] When the break is taken into consideration, the gains ḡ1 and ḡ2 both fall below that for the long-sample model without the break (ḡLS). This supports the proposition that the estimated gain parameter may be ‘too high’ in estimates over long samples with regime shifts that are ignored. The gain in the pre-inflation-targeting period, ḡ1, is 0.0004 and the gain after the regime shift, ḡ2, is lower at 0.0003. This is consistent with the notion that the inflation-targeting regime is a more stable period in many respects than that which came before.
Footnote
Other parameters may also have shifted in response to the move to inflation targeting, but it is beyond the scope of this paper to test for such breaks. [14]